Eksponen 4. Fungsi Eksponen dan Grafiknya

A. Definisi Fungsi Eksponen

Fungsi eksponen adalah fungsi yang variabel bebasnya berupa pangkat. Fungsi ini memetakan setiap bilangan real $x$ ke bilangan real $a^x$, dengan $a > 0$ dan $a\ne 1$.
Bentuk umum fungsi eksponen didefinisikan sebagai berikut:
$y=f(x)=ka^x$; $a > 0$ dan $a\ne 1$
Dengan:

• $x$ adalah variabel bebas, dengan daerah asal (domain) $D_f=\{x|x\in R\}$.
• $a$ adalah bilangan pokok atau basis eksponen, dengan ketentuan $a > 0$ dan $a\ne 1$.
• $y$ adalah variabel tak bebas, dengan daerah hasil (range) $R_f=\{y|y>0,y\in R\}$.
• $k$ adalah konstanta sembarang.

B. Grafik Fungsi Eksponen

Grafik fungsi eksponen $y=f(x)=a^x$ dikelompokkan menjadi dua macam berdasarkan bilangan pokok $a$, yaitu:

1. Grafik fungsi eksponen dengan bilangan pokok $a > 1$ (perhatikan contoh 1).
2. Grafik fungsi eksponen dengan bilangan pokok $0 < a < 1$ (perhatikan contoh 2).

Contoh 1.
Gambarkanlah grafik fungsi eksponen $y=f(x)=2^x$.
Penyelesaian:
Kita buat tabel yang menunjukkan hubungan antara nilai $x$ dengan nilai $y=2^x$.

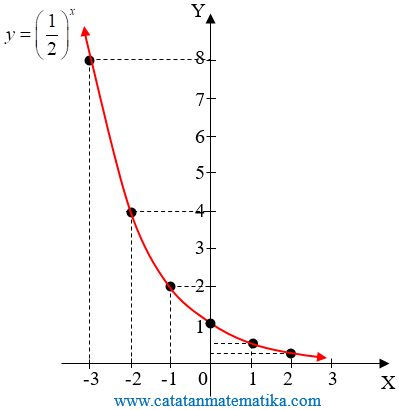
Gambarkan titik-titik koordinat $(x,y)$ pada bidang cartesius. Kemudian hubungkan antara dua titik yang berdekatan dengan kurva yang mulus, sehingga diperoleh grafik fungsi eksponen $y=2^x$.


Contoh 2.
Gambarkanlah grafik fungsi eksponen $y=f(x)=\left( \frac{1}{2} \right)^x$.
Penyelesaian:
Kita buat tabel yang menunjukkan hubungan antara nilai $x$ dengan nilai $y=\left( \frac{1}{2} \right)^x$.

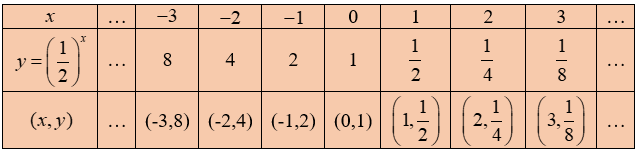
Gambarkan titik-titik koordinat $(x,y)$ pada bidang cartesius. Kemudian hubungkan antara dua titik yang berdekatan dengan kurva yang mulus, sehingga diperoleh grafik fungsi eksponen $y=\left( \frac{1}{2} \right)^x$.

C. Sifat-sifat Fungsi Eksponen

Berdasarkan contoh 1 dan contoh 2 grafik fungsi eksponen $y=a^x$ secara umum ditunjukkan pada gambar berikut.

Dari grafik di atas, dapat dituliskan sifat-sifat fungsi eksponen $y=a^x$; $a\ne 1$ sebagai berikut:

1. Fungsi $y=a^x$ selalu memotong sumbu Y di titik $(0,1)$.
2. Fungsi $y=a^x$ adalah fungsi kontinu.
3. Sumbu X tidak pernah dipotong oleh fungsi $y={{a}^{x}}$, melainkan hanya didekati. Kita katakan bahwa sumbu X sebagai asimtot datar.
4. Fungsi $y=a^x$ adalah fungsi satu-satu dan memiliki invers. Invers dari fungsi eksponen adalah fungsi logaritma.
5. Fungsi $y=a^x$ untuk $a > 1$ adalah fungsi naik.
6. Fungsi $y=a^x$ untuk $0 < a < 1$ adalah fungsi turun.
7. Grafik fungsi $y=a^x$ dan $y=\left( \frac{1}{a} \right)^x$ adalah setangkup (simetris) terhadap sumbu Y.

D. Menentukan Persamaan Fungsi Eksponen

Untuk menentukan persamaan dari grafik fungsi eksponen, kita dapat menggunakan beberapa keterangan yang diberikan pada gambar seperti melalui beberapa titik, asimtot datar dan bentuk persamaannya.
Contoh 3.
Perhatikan gambar!

Tentukan persamaan dari grafik fungsi eksponen di atas.
Penyelesaian:
Berdasarkan grafik dan keterangan pada soal, diperoleh bahwa persamaan grafiknya adalah:
$y=a^x+b$
Grafik melalui titik $(0,2)$ maka:
$\begin{align}y &= a^x+b \\ 2 &= a^0+b \\ 2 &= 1+b \\ 1 &= b \end{align}$
Grafik melalui titik $(2,5)$ maka:
$\begin{align}y &= a^x+b \\ 5 &= a^2+1 \\ 4 &= a^2 \\ 2^2 &= a^2 \\ 2 &= a \end{align}$
$y=a^x+b \to y=2^x+1$
Jadi, persamaan dari grafik fungsi tersebut adalah $y=2^x+1$.

Contoh 4.
Perhatikan gambar!

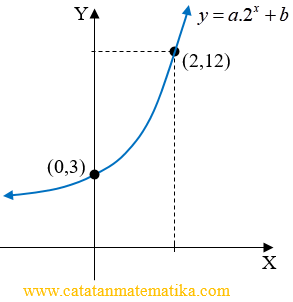
Tentukan persamaan dari grafik fungsi eksponen di atas.
Penyelesaian:
Berdasarkan grafik dan keterangan pada soal, diperoleh bahwa persamaan grafiknya adalah:
$y=a.2^x+b$
Grafik melalui titik $(0,3)$ maka:
$\begin{align}y &= a.2^x+b \\ 3 &= a.2^0+b \\ 3 &= a+b\,..........\,(1) \end{align}$
Grafik melalui titik $(2,5)$ maka:
$\begin{align}y &= a.2^x+b \\ 12 &= a.2^2+b \\ 12 &= 4a+b\,...........\,(2) \end{align}$
Kurangkan persamaan (2) dengan (1):
$\begin{align}4a+b &= 12 \\ a+b &= 3 \end{align}$
-------------------- (-)
$3a=9\to a=3$
Substitusi $a=3$ ke persamaan (1):
$\begin{align}a+b &= 3 \\ 3+b &= 3 \\ b &= 0 \end{align}$
$\begin{align}y &= a.2^x+b \\ y &= 3.2^x+0 \\ y &= 3.2^x \end{align}$
Jadi, persamaan dari grafik fungsi tersebut adalah $y={{3.2}^{x}}$.

E. Soal Latihan

1.	Gambarlah grafik $y=3^x$.
2.	Gambarlah grafik $y=\left( \frac{1}{3} \right)^x$.
3.	Perhatikan gambar!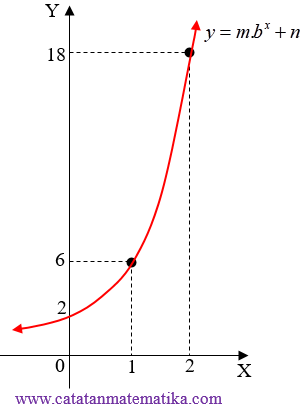 Tentukan persamaan fungsi dari grafik tersebut.
4.	Perhatikan gambar! Fungsi pada grafik di atas adalah $f(x)=3.a^x-1$. Tentukan nilai $a$.
5.	Diketahui $f(x)=2^{2x}+2^{x+1}-3$ dan $g(x)=2^x+3$. Tentukan bentuk sederhana dari $\frac{f(x)}{g(x)}$.

By: Catatan Matematika

Semoga postingan: Eksponen 4. Fungsi Eksponen dan Grafiknya ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :