Kumpulan Soal - Aturan Sinus + Pembahasan
Berikut ini adalah kumpulan Soal dan Pembahasan Aturan Sinus yaitu salah satu sub topik materi TRIGONOMETRI pada bidang studi Matematika. Selamat belajar ya...!
A. $30^\circ $
B. $45^\circ $
C. $55^\circ $
D. $60^\circ $
E. $78^\circ $
Jawaban: A
A. 5 cm
B. $5\sqrt{3}$ cm
C. $10\sqrt{2}$ cm
D. $10\sqrt{3}$ cm
E. $\frac{10}{3}\sqrt{3}$ cm
BC = 10 = a, AC = b = …?
$\begin{align}\frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{b}{\sin 45^\circ } &=\frac{10}{\sin 30^\circ } \\ \frac{b}{\frac{1}{2}\sqrt{2}} &=\frac{10}{\frac{1}{2}} \\ b &=10\sqrt{2} \end{align}$
Jawaban: C

BC : AC = ….
A. 3 : 4
B. 4 : 3
C. $\sqrt{2}:\sqrt{3}$
D. $\sqrt{3}:2\sqrt{2}$
E. $\sqrt{3}:\sqrt{2}$
$\begin{align} \frac{a}{\sin A} &=\frac{b}{\sin B} \\ \frac{a}{\sin 45^\circ } &=\frac{b}{\sin 60^\circ } \\ \frac{a}{b} &=\frac{\sin 45^\circ }{\sin 60^\circ } \\ \frac{a}{b} &=\frac{\frac{1}{2}\sqrt{2}}{\frac{1}{2}\sqrt{3}} \\ \frac{a}{b} &=\frac{\sqrt{2}}{\sqrt{3}} \end{align}$
Jawaban: C
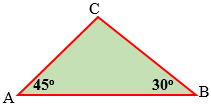
Dua orang mulai berjalan masing-masing dari titik A dan titik B pada saat yang sama. Supaya keduanya sampai di titik C pada saat yang sama, maka kecepatan berjalan dari titik A harus ….
A. 2 kali kecepatan orang yang dari B
B. $\frac{1}{2}\sqrt{2}$ kali kecepatan orang yang dari B.
C. $\sqrt{2}$ kali kecepatan orang yang dari B.
D. $2\sqrt{2}$ kali kecepatan orang yang dari B.
E. $\sqrt{3}$ kali kecepatan orang yang dari B.
$\begin{align} \frac{a}{\sin A} &=\frac{b}{\sin B} \\ \frac{\sin B}{\sin A} &=\frac{b}{a} \end{align}$
$\begin{align} {{t}_{a}} &={{t}_{b}} \\ \frac{{{s}_{a}}}{{{v}_{a}}} &=\frac{{{s}_{b}}}{{{v}_{b}}} \\ \frac{b}{{{v}_{a}}} &=\frac{a}{{{v}_{b}}} \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{b}{a} \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{\sin B}{\sin A} \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{\sin 30^\circ }{\sin 45^\circ } \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{\frac{1}{2}}{\frac{1}{2}\sqrt{2}} \\ {{v}_{a}} &=\frac{1}{\sqrt{2}}.{{v}_{b}} \\ {{v}_{a}} &=\frac{1}{2}\sqrt{2}.{{v}_{b}} \end{align}$
Jawaban: B
A. $30^\circ $
B. $45^\circ $
C. $75^\circ $
D. $105^\circ $
E. $120^\circ $
$\begin{align} \frac{q}{\sin Q} &=\frac{p}{\sin P} \\ \frac{3}{\sin Q} &=\frac{\frac{3\sqrt{6}}{2}}{\sin 60^\circ } \\ \frac{3}{\sin Q} &=\frac{\frac{3}{2}\sqrt{6}}{\frac{1}{2}\sqrt{3}} \\ \frac{3}{\sin Q} &=3\sqrt{2} \\ 3\sqrt{2}.\sin Q &=3 \\ \sin Q &=\frac{1}{\sqrt{2}} \\ \sin Q &=\frac{1}{2}\sqrt{2} \\ Q &=45^\circ \end{align}$
$\begin{align} P+Q+R &=180^\circ \\ 60^\circ +45^\circ +R & =180^\circ \\ 105^\circ +R &=180^\circ \\ R &=180^\circ -105^\circ \\ R &=75^\circ \end{align}$
Jawaban: C
A. $\frac{1}{2}$
B. $\frac{1}{2}\sqrt{2}$
C. $\frac{1}{2}\sqrt{3}$
D. $\frac{1}{2}\sqrt{5}$
E. 1
$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{2}{\sin B} &=\frac{2\sqrt{2}}{\sin 45^\circ } \\ \frac{1}{\sin B} &=\frac{\sqrt{2}}{\frac{1}{2}\sqrt{2}} \\ \frac{1}{\sin B} &=\frac{2}{1} \\ \sin B &=\frac{1}{2} \\ B &=30^\circ \end{align}$
$\cos B =\cos 30^\circ =\frac{1}{2}\sqrt{3}$
Jawaban: C

Nilai dari sin D = ….
A. $\frac{1}{16}\sqrt{6}$
B. $\frac{1}{8}\sqrt{6}$
C. $\frac{1}{4}\sqrt{6}$
D. $\frac{1}{3}\sqrt{6}$
E. $\frac{1}{5}\sqrt{6}$
$\begin{align} \frac{BC}{\sin \angle BAC} &=\frac{AC}{\sin \angle ABC} \\ \frac{BC}{\sin 30^\circ } &=\frac{2}{\sin 45^\circ } \\ \frac{BC}{\frac{1}{2}} &=\frac{2}{\frac{1}{2}\sqrt{2}} \\ BC &=\frac{2}{\sqrt{2}} \\ BC &=\sqrt{2} \end{align}$
Perhatikan segitiga BCD:
$\begin{align} \frac{BC}{\sin \angle BDC} &=\frac{BD}{\sin \angle BCD} \\ \frac{\sqrt{2}}{\sin D} &=\frac{4}{\sin 60^\circ } \\ \frac{\sqrt{2}}{\sin D} &=\frac{4}{\frac{1}{2}\sqrt{3}} \\ 4\sin D &=\frac{1}{2}\sqrt{6} \\ \sin D &=\frac{1}{8}\sqrt{6} \end{align}$
Jawaban: B
A. $\frac{1}{6}\sqrt{2}$
B. $\frac{1}{6}\sqrt{6}$
C. $\frac{1}{6}\sqrt{7}$
D. $\frac{1}{3}\sqrt{2}$
E. $\frac{1}{3}\sqrt{7}$
$\begin{align} \frac{a}{\sin A} &=\frac{b}{\sin B} \\ \frac{4}{\sin A} &=\frac{6}{\sin 45^\circ } \\ \frac{4}{\sin A} &=\frac{6}{\frac{1}{2}\sqrt{2}} \\ 6\sin A &=2\sqrt{2} \\ \sin A &=\frac{\sqrt{2}}{3} \end{align}$
$\sin A=\frac{de}{mi}=\frac{\sqrt{2}}{3}$
$\begin{align} sa &=\sqrt{m{{i}^{2}}-d{{e}^{2}}} \\ & =\sqrt{{{3}^{2}}-{{(\sqrt{2})}^{2}}} \\ sa &=\sqrt{7} \end{align}$
$\cos A=\frac{sa}{mi}=\frac{\sqrt{7}}{3}$
Jawaban: E
A. 8
B. 2
C. $2\sqrt{6}$
D. $2\sqrt{2}$
E. $2\sqrt{10}$
PQ = r = …
$\begin{align} \frac{q}{\sin Q} &=\frac{p}{\sin P} \\ \frac{\sqrt{2}}{\sin Q} &=\frac{\sqrt{6}}{\sin 60^\circ } \\ \frac{\sqrt{2}}{\sin Q} &=\frac{\sqrt{6}}{\frac{1}{2}\sqrt{3}} \\ \sqrt{6}.\sin Q &=\frac{1}{2}\sqrt{6} \\ \sin Q &=\frac{1}{2} \\ Q &=30^\circ \end{align}$
$\begin{align} P+Q+R &=180^\circ \\ 60^\circ +30^\circ +R &=180^\circ \\ R &=90^\circ \end{align}$
$\begin{align} \frac{r}{\sin R} &=\frac{q}{\sin Q} \\ \frac{r}{\sin 90^\circ } &=\frac{\sqrt{2}}{\sin 30^\circ } \\ \frac{r}{1} &=\frac{\sqrt{2}}{\frac{1}{2}} \\ r &=2\sqrt{2} \end{align}$
Jawaban: D
A. $\frac{1}{2}\sqrt{2}$
B. $\frac{1}{2}\sqrt{3}$
C. 1
D. $-1$
E. 0
$\tan B=\tan 45^\circ =1$
Jawaban: C
A. $9\sqrt{3}$
B. $\frac{9}{2}\sqrt{3}$
C. $3\sqrt{6}$
D. $\frac{1}{2}\sqrt{6}$
E. $3\sqrt{3}$
Jawaban: C
A. $3\sqrt{6}$
B. $9\sqrt{2}$
C. $\frac{9}{2}\sqrt{6}$
D. $9\sqrt{6}$
E. $6\sqrt{6}$
Jawaban: A
A. 5
B. $10\sqrt{2}$
C. $5\sqrt{2}$
D. 10
E. 20
$\begin{align} \frac{r}{\sin R} &=\frac{p}{\sin P} \\ \frac{r}{\sin 30^\circ } &=\frac{10}{\sin 45^\circ } \\ \frac{r}{\frac{1}{2}} &=\frac{10}{\frac{1}{2}\sqrt{2}} \\ r &=\frac{10}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ r &=5\sqrt{2} \end{align}$
Jawaban: C
A. $6\sqrt{2}$
B. $6\sqrt{3}$
C. $6\sqrt{6}$
D. $12\sqrt{3}$
E. $12\sqrt{6}$
BC = a = …?
$\begin{align} A+B+C &=180^\circ \\ 60^\circ +75^\circ +C &=180^\circ \\ C &=45^\circ \end{align}$
$\begin{align} \frac{a}{\sin A} &=\frac{c}{\sin C} \\ \frac{a}{\sin 60^\circ } &=\frac{12}{\sin 45^\circ } \\ \frac{a}{\frac{1}{2}\sqrt{3}} &=\frac{12}{\frac{1}{2}\sqrt{2}} \\ a &=\frac{12\sqrt{3}}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ a &=6\sqrt{6} \\ BC &=6\sqrt{6} \end{align}$
Jawaban: C
A. $8\sqrt{2}$
B. 6
C. $5\sqrt{2}$
D. $4\sqrt{2}$
E. $3\sqrt{2}$
RT = s = …?
$\begin{align} R+S+T &=180^\circ \\ 30^\circ +S+105^\circ &=180^\circ \\ S &=45^\circ \end{align}$
$\begin{align} \frac{s}{\sin S} &=\frac{r}{\sin R} \\ \frac{s}{\sin 45^\circ } &=\frac{4}{\sin 30^\circ } \\ \frac{s}{\frac{1}{2}\sqrt{2}} &=\frac{4}{\frac{1}{2}} \\ s &=4\sqrt{2} \end{align}$
Jawaban: D
A. $\frac{2}{5}\sqrt{5}$
B. $\frac{1}{3}\sqrt{5}$
C. $\frac{1}{2}\sqrt{3}$
D. $\frac{2}{3}$
E. $\frac{1}{2}$
$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{4}{\sin B} &=\frac{3}{\frac{1}{2}} \\ 3\sin B &=2 \\ \sin B &=\frac{2}{3} \end{align}$
$\sin B=\frac{de}{mi}=\frac{2}{3}$
$\begin{align}sa &=\sqrt{m{{i}^{2}}-d{{e}^{2}}} \\ &=\sqrt{{{3}^{2}}-{{2}^{2}}} \\ sa &=\sqrt{5} \end{align}$
$\cos B=\frac{sa}{mi}=\frac{\sqrt{5}}{3}$
Jawaban: B
A. $2\sqrt{2}$
B. $3\sqrt{2}$
C. $4\sqrt{2}$
D. 6
E. 8
BC = 4 = a, AC = b = …?
$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{b}{\sin 45^\circ } &=\frac{4}{\sin 30^\circ } \\ \frac{b}{\frac{1}{2}\sqrt{2}} &=\frac{4}{\frac{1}{2}} \\ b &=4\sqrt{2} \end{align}$
Jawaban: C
Soal Aturan Sinus No. 1
Pada segitiga ABC, jika diketahui a = 8 cm, b = $4\sqrt{2}$ cm, dan $\angle A=45{}^\circ $, maka $\angle B$ = …A. $30^\circ $
B. $45^\circ $
C. $55^\circ $
D. $60^\circ $
E. $78^\circ $
Penyelesaian: Lihat/Tutup
$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{4\sqrt{2}}{\sin B} &=\frac{8}{\sin 45^\circ } \\ \frac{4\sqrt{2}}{\sin B} &=\frac{8}{\frac{1}{2}\sqrt{2}} \\ 8\sin B &=4 \\ \sin B &=\frac{4}{8}=\frac{1}{2} \\ B &=30^\circ \end{align}$Jawaban: A
Soal Aturan Sinus No. 2
Diketahui segitiga ABC dengan $\angle A=30^\circ $, $\angle C=105^\circ $, dan BC = 10 cm. Panjang AC = …. A. 5 cm
B. $5\sqrt{3}$ cm
C. $10\sqrt{2}$ cm
D. $10\sqrt{3}$ cm
E. $\frac{10}{3}\sqrt{3}$ cm
Penyelesaian: Lihat/Tutup
$\begin{align} \angle A+\angle B+\angle C &=180^\circ \\ 30^\circ +\angle B+105^\circ &=180^\circ \\ \angle B &=45^\circ \end{align}$BC = 10 = a, AC = b = …?
$\begin{align}\frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{b}{\sin 45^\circ } &=\frac{10}{\sin 30^\circ } \\ \frac{b}{\frac{1}{2}\sqrt{2}} &=\frac{10}{\frac{1}{2}} \\ b &=10\sqrt{2} \end{align}$
Jawaban: C
Soal Aturan Sinus No. 3
Perhatikan gambar berikut!
BC : AC = ….
A. 3 : 4
B. 4 : 3
C. $\sqrt{2}:\sqrt{3}$
D. $\sqrt{3}:2\sqrt{2}$
E. $\sqrt{3}:\sqrt{2}$
Penyelesaian: Lihat/Tutup
BC : AC = a : b = …?$\begin{align} \frac{a}{\sin A} &=\frac{b}{\sin B} \\ \frac{a}{\sin 45^\circ } &=\frac{b}{\sin 60^\circ } \\ \frac{a}{b} &=\frac{\sin 45^\circ }{\sin 60^\circ } \\ \frac{a}{b} &=\frac{\frac{1}{2}\sqrt{2}}{\frac{1}{2}\sqrt{3}} \\ \frac{a}{b} &=\frac{\sqrt{2}}{\sqrt{3}} \end{align}$
Jawaban: C
Soal Aturan Sinus No. 4
Perhatikan gambar berikut!
Dua orang mulai berjalan masing-masing dari titik A dan titik B pada saat yang sama. Supaya keduanya sampai di titik C pada saat yang sama, maka kecepatan berjalan dari titik A harus ….
A. 2 kali kecepatan orang yang dari B
B. $\frac{1}{2}\sqrt{2}$ kali kecepatan orang yang dari B.
C. $\sqrt{2}$ kali kecepatan orang yang dari B.
D. $2\sqrt{2}$ kali kecepatan orang yang dari B.
E. $\sqrt{3}$ kali kecepatan orang yang dari B.
Penyelesaian: Lihat/Tutup
Aturan sinus:$\begin{align} \frac{a}{\sin A} &=\frac{b}{\sin B} \\ \frac{\sin B}{\sin A} &=\frac{b}{a} \end{align}$
$\begin{align} {{t}_{a}} &={{t}_{b}} \\ \frac{{{s}_{a}}}{{{v}_{a}}} &=\frac{{{s}_{b}}}{{{v}_{b}}} \\ \frac{b}{{{v}_{a}}} &=\frac{a}{{{v}_{b}}} \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{b}{a} \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{\sin B}{\sin A} \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{\sin 30^\circ }{\sin 45^\circ } \\ \frac{{{v}_{a}}}{{{v}_{b}}} &=\frac{\frac{1}{2}}{\frac{1}{2}\sqrt{2}} \\ {{v}_{a}} &=\frac{1}{\sqrt{2}}.{{v}_{b}} \\ {{v}_{a}} &=\frac{1}{2}\sqrt{2}.{{v}_{b}} \end{align}$
Jawaban: B
Soal Aturan Sinus No. 5
Diketahui segitiga PQR dengan PR = 3 cm dan QR = $\frac{3\sqrt{6}}{2}$, $\angle P=60^\circ $. Besar sudut R adalah ….A. $30^\circ $
B. $45^\circ $
C. $75^\circ $
D. $105^\circ $
E. $120^\circ $
Penyelesaian: Lihat/Tutup
PR = q = 3 cm, QR = p = $\frac{3\sqrt{6}}{2}$, $\angle P=60^\circ $$\begin{align} \frac{q}{\sin Q} &=\frac{p}{\sin P} \\ \frac{3}{\sin Q} &=\frac{\frac{3\sqrt{6}}{2}}{\sin 60^\circ } \\ \frac{3}{\sin Q} &=\frac{\frac{3}{2}\sqrt{6}}{\frac{1}{2}\sqrt{3}} \\ \frac{3}{\sin Q} &=3\sqrt{2} \\ 3\sqrt{2}.\sin Q &=3 \\ \sin Q &=\frac{1}{\sqrt{2}} \\ \sin Q &=\frac{1}{2}\sqrt{2} \\ Q &=45^\circ \end{align}$
$\begin{align} P+Q+R &=180^\circ \\ 60^\circ +45^\circ +R & =180^\circ \\ 105^\circ +R &=180^\circ \\ R &=180^\circ -105^\circ \\ R &=75^\circ \end{align}$
Jawaban: C
Soal Aturan Sinus No. 6
Suatu segitiga ABC dan diketahui $\angle A=45^\circ $, AC = 2 cm, BC = $2\sqrt{2}$ maka nilai $\cos \angle B$ = …A. $\frac{1}{2}$
B. $\frac{1}{2}\sqrt{2}$
C. $\frac{1}{2}\sqrt{3}$
D. $\frac{1}{2}\sqrt{5}$
E. 1
Penyelesaian: Lihat/Tutup
$\angle A=45^\circ $, AC = b = 2 cm, BC = a = $2\sqrt{2}$$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{2}{\sin B} &=\frac{2\sqrt{2}}{\sin 45^\circ } \\ \frac{1}{\sin B} &=\frac{\sqrt{2}}{\frac{1}{2}\sqrt{2}} \\ \frac{1}{\sin B} &=\frac{2}{1} \\ \sin B &=\frac{1}{2} \\ B &=30^\circ \end{align}$
$\cos B =\cos 30^\circ =\frac{1}{2}\sqrt{3}$
Jawaban: C
Soal Aturan Sinus No. 7
Perhatikan gambar berikut!
Nilai dari sin D = ….
A. $\frac{1}{16}\sqrt{6}$
B. $\frac{1}{8}\sqrt{6}$
C. $\frac{1}{4}\sqrt{6}$
D. $\frac{1}{3}\sqrt{6}$
E. $\frac{1}{5}\sqrt{6}$
Penyelesaian: Lihat/Tutup
Perhatikan segitiga ABC:$\begin{align} \frac{BC}{\sin \angle BAC} &=\frac{AC}{\sin \angle ABC} \\ \frac{BC}{\sin 30^\circ } &=\frac{2}{\sin 45^\circ } \\ \frac{BC}{\frac{1}{2}} &=\frac{2}{\frac{1}{2}\sqrt{2}} \\ BC &=\frac{2}{\sqrt{2}} \\ BC &=\sqrt{2} \end{align}$
Perhatikan segitiga BCD:
$\begin{align} \frac{BC}{\sin \angle BDC} &=\frac{BD}{\sin \angle BCD} \\ \frac{\sqrt{2}}{\sin D} &=\frac{4}{\sin 60^\circ } \\ \frac{\sqrt{2}}{\sin D} &=\frac{4}{\frac{1}{2}\sqrt{3}} \\ 4\sin D &=\frac{1}{2}\sqrt{6} \\ \sin D &=\frac{1}{8}\sqrt{6} \end{align}$
Jawaban: B
Soal Aturan Sinus No. 8
Pada segitiga ABC diketahui sisi $a=4$, sisi $b=6$ dan sudut B = $45^\circ $. Nilai kosinus sudut A adalah …..A. $\frac{1}{6}\sqrt{2}$
B. $\frac{1}{6}\sqrt{6}$
C. $\frac{1}{6}\sqrt{7}$
D. $\frac{1}{3}\sqrt{2}$
E. $\frac{1}{3}\sqrt{7}$
Penyelesaian: Lihat/Tutup
$a=4$, sisi $b=6$, $\angle B$ = $45^\circ $, $\cos A$ = …?$\begin{align} \frac{a}{\sin A} &=\frac{b}{\sin B} \\ \frac{4}{\sin A} &=\frac{6}{\sin 45^\circ } \\ \frac{4}{\sin A} &=\frac{6}{\frac{1}{2}\sqrt{2}} \\ 6\sin A &=2\sqrt{2} \\ \sin A &=\frac{\sqrt{2}}{3} \end{align}$
$\sin A=\frac{de}{mi}=\frac{\sqrt{2}}{3}$
$\begin{align} sa &=\sqrt{m{{i}^{2}}-d{{e}^{2}}} \\ & =\sqrt{{{3}^{2}}-{{(\sqrt{2})}^{2}}} \\ sa &=\sqrt{7} \end{align}$
$\cos A=\frac{sa}{mi}=\frac{\sqrt{7}}{3}$
Jawaban: E
Soal Aturan Sinus No. 9
Diketahui segitiga PQR dengan panjang QR = $\sqrt{6}$, PR = $\sqrt{2}$ dan $\angle P=60^\circ $, maka panjang PQ = …A. 8
B. 2
C. $2\sqrt{6}$
D. $2\sqrt{2}$
E. $2\sqrt{10}$
Penyelesaian: Lihat/Tutup
QR = p = $\sqrt{6}$, PR = q = $\sqrt{2}$ dan $\angle P=60^\circ $PQ = r = …
$\begin{align} \frac{q}{\sin Q} &=\frac{p}{\sin P} \\ \frac{\sqrt{2}}{\sin Q} &=\frac{\sqrt{6}}{\sin 60^\circ } \\ \frac{\sqrt{2}}{\sin Q} &=\frac{\sqrt{6}}{\frac{1}{2}\sqrt{3}} \\ \sqrt{6}.\sin Q &=\frac{1}{2}\sqrt{6} \\ \sin Q &=\frac{1}{2} \\ Q &=30^\circ \end{align}$
$\begin{align} P+Q+R &=180^\circ \\ 60^\circ +30^\circ +R &=180^\circ \\ R &=90^\circ \end{align}$
$\begin{align} \frac{r}{\sin R} &=\frac{q}{\sin Q} \\ \frac{r}{\sin 90^\circ } &=\frac{\sqrt{2}}{\sin 30^\circ } \\ \frac{r}{1} &=\frac{\sqrt{2}}{\frac{1}{2}} \\ r &=2\sqrt{2} \end{align}$
Jawaban: D
Soal Aturan Sinus No. 10
Diketahui segitiga ABC dengan panjang sisi a = $3\sqrt{2}$ cm, b = 6 cm, dan $\angle A=30^\circ $ maka nilai $\tan \angle B$ = …A. $\frac{1}{2}\sqrt{2}$
B. $\frac{1}{2}\sqrt{3}$
C. 1
D. $-1$
E. 0
Penyelesaian: Lihat/Tutup
$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{6}{\sin B} &=\frac{3\sqrt{2}}{\sin 30^\circ } \\ \frac{6}{\sin B} &=\frac{3\sqrt{2}}{\frac{1}{2}} \\ 3\sqrt{2}.\sin B &=3 \\ \sin B &=\frac{1}{\sqrt{2}}=\frac{1}{2}\sqrt{2} \\ B &=45^\circ \end{align}$$\tan B=\tan 45^\circ =1$
Jawaban: C
Soal Aturan Sinus No. 11
Dalam segitiga ABC diketahui a = 9, $\angle A=60^\circ $, $\angle B=45^\circ $ maka b = ….A. $9\sqrt{3}$
B. $\frac{9}{2}\sqrt{3}$
C. $3\sqrt{6}$
D. $\frac{1}{2}\sqrt{6}$
E. $3\sqrt{3}$
Penyelesaian: Lihat/Tutup
$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{b}{\sin 45^\circ } &=\frac{9}{\sin 60^\circ } \\ \frac{b}{\frac{1}{2}\sqrt{2}} &=\frac{9}{\frac{1}{2}\sqrt{3}} \\ b &=\frac{9\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ b &=3\sqrt{6} \end{align}$Jawaban: C
Soal Aturan Sinus No. 12
Suatu segitiga PQR dengan sisi p = 9 cm, $\angle P=120^\circ $, $\angle Q=45^\circ $, maka panjang sisi q = … cm.A. $3\sqrt{6}$
B. $9\sqrt{2}$
C. $\frac{9}{2}\sqrt{6}$
D. $9\sqrt{6}$
E. $6\sqrt{6}$
Penyelesaian: Lihat/Tutup
$\begin{align} \frac{q}{\sin Q} &=\frac{p}{\sin P} \\ \frac{q}{\sin 45^\circ } &=\frac{9}{\sin 120^\circ } \\ \frac{q}{\frac{1}{2}\sqrt{2}} &=\frac{9}{\sin (180^\circ -60^\circ )} \\ q &=\frac{\frac{9\sqrt{2}}{2}}{\sin 60^\circ } \\ q &=\frac{\frac{9\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}} \\ q &=\frac{9\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ q &=3\sqrt{6} \end{align}$Jawaban: A
Soal Aturan Sinus No. 13
Diketahui segitiga PQR dimana p = 10 cm, $\angle P=45^\circ $, dan $\angle Q=105^\circ $, panjang sisi r = … cm.A. 5
B. $10\sqrt{2}$
C. $5\sqrt{2}$
D. 10
E. 20
Penyelesaian: Lihat/Tutup
$\begin{align} P+Q+R &=180^\circ \\ 45^\circ +105^\circ +R &=180^\circ \\ R &=30^\circ \end{align}$$\begin{align} \frac{r}{\sin R} &=\frac{p}{\sin P} \\ \frac{r}{\sin 30^\circ } &=\frac{10}{\sin 45^\circ } \\ \frac{r}{\frac{1}{2}} &=\frac{10}{\frac{1}{2}\sqrt{2}} \\ r &=\frac{10}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ r &=5\sqrt{2} \end{align}$
Jawaban: C
Soal Aturan Sinus No. 14
Diketahui segitiga ABC dengan besar $\angle A=60^\circ $, $\angle B=75^\circ $, dan panjang AB = 12 cm. Panjang BC adalah … cm.A. $6\sqrt{2}$
B. $6\sqrt{3}$
C. $6\sqrt{6}$
D. $12\sqrt{3}$
E. $12\sqrt{6}$
Penyelesaian: Lihat/Tutup
$\angle A=60^\circ $, $\angle B=75^\circ $, AB = c = 12 cm,BC = a = …?
$\begin{align} A+B+C &=180^\circ \\ 60^\circ +75^\circ +C &=180^\circ \\ C &=45^\circ \end{align}$
$\begin{align} \frac{a}{\sin A} &=\frac{c}{\sin C} \\ \frac{a}{\sin 60^\circ } &=\frac{12}{\sin 45^\circ } \\ \frac{a}{\frac{1}{2}\sqrt{3}} &=\frac{12}{\frac{1}{2}\sqrt{2}} \\ a &=\frac{12\sqrt{3}}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ a &=6\sqrt{6} \\ BC &=6\sqrt{6} \end{align}$
Jawaban: C
Soal Aturan Sinus No. 15
Pada segitiga RST diketahui ST = 4 cm, $\angle R=30^\circ $ dan $\angle T=105^\circ $. Panjang sisi RT adalah … cm.A. $8\sqrt{2}$
B. 6
C. $5\sqrt{2}$
D. $4\sqrt{2}$
E. $3\sqrt{2}$
Penyelesaian: Lihat/Tutup
ST = r = 4 cm, $\angle R=30^\circ $, $\angle T=105^\circ $RT = s = …?
$\begin{align} R+S+T &=180^\circ \\ 30^\circ +S+105^\circ &=180^\circ \\ S &=45^\circ \end{align}$
$\begin{align} \frac{s}{\sin S} &=\frac{r}{\sin R} \\ \frac{s}{\sin 45^\circ } &=\frac{4}{\sin 30^\circ } \\ \frac{s}{\frac{1}{2}\sqrt{2}} &=\frac{4}{\frac{1}{2}} \\ s &=4\sqrt{2} \end{align}$
Jawaban: D
Soal Aturan Sinus No. 16
Ditentukan segitiga ABC dengan panjang sisi BC = 3 cm, sisi AC = 4 cm dan $\sin A=\frac{1}{2}$. Nilai cos B = …A. $\frac{2}{5}\sqrt{5}$
B. $\frac{1}{3}\sqrt{5}$
C. $\frac{1}{2}\sqrt{3}$
D. $\frac{2}{3}$
E. $\frac{1}{2}$
Penyelesaian: Lihat/Tutup
BC = a = 3 cm, AC = b = 4 cm dan $\sin A=\frac{1}{2}$$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{4}{\sin B} &=\frac{3}{\frac{1}{2}} \\ 3\sin B &=2 \\ \sin B &=\frac{2}{3} \end{align}$
$\sin B=\frac{de}{mi}=\frac{2}{3}$
$\begin{align}sa &=\sqrt{m{{i}^{2}}-d{{e}^{2}}} \\ &=\sqrt{{{3}^{2}}-{{2}^{2}}} \\ sa &=\sqrt{5} \end{align}$
$\cos B=\frac{sa}{mi}=\frac{\sqrt{5}}{3}$
Jawaban: B
Soal Aturan Sinus No. 17
Pada segitiga ABC. Diketahui $\angle C=105^\circ $, $\angle A=30^\circ $ dan BC = 4. Panjang AC = ….A. $2\sqrt{2}$
B. $3\sqrt{2}$
C. $4\sqrt{2}$
D. 6
E. 8
Penyelesaian: Lihat/Tutup
$\begin{align} \angle A+\angle B+\angle C &=180^\circ \\ 30^\circ +\angle B+105^\circ &=180^\circ \\ \angle B+135^\circ =180^\circ \\ \angle B &=45^\circ \end{align}$BC = 4 = a, AC = b = …?
$\begin{align} \frac{b}{\sin B} &=\frac{a}{\sin A} \\ \frac{b}{\sin 45^\circ } &=\frac{4}{\sin 30^\circ } \\ \frac{b}{\frac{1}{2}\sqrt{2}} &=\frac{4}{\frac{1}{2}} \\ b &=4\sqrt{2} \end{align}$
Jawaban: C

Mantap sekali, terima kasih..
ReplyDelete