Menggambar Grafik Persamaan Garis Lurus

MENGGAMBAR GRAFIK PERSAMAAN GARIS LURUS
KONSEP DASAR:
Melalui dua titik dapat dilukis sebuah garis lurus.
Contoh 1
Gambarlah grafik persamaan garis lurus y = 4
Penyelesaian:
Langkah 1. Tentukan dua titik sembarang
Jika x = 0 maka y = 4, diperoleh titik (0,4)
Jika x = 4 maka y = 4, diperoleh titik (4,4)
Langkah 2. Letakkan titik (0,4) dan (4,4) pada bidang koordinat kartesius
Langkah 3. Hubungkan titik (0,4) dan (4,4) maka diperolehlah grafik garis y = 4

TIPS: garis y = k adalah garis yang sejajar dengan sumbu X dan melalui titik (0,k).
Contoh 2
Gambarlah grafik persamaan garis lurus x = -3.
Penyelesaian:
Langkah 1. Tentukan dua titik sembarang
Jika y = -2 maka x = -3 diperoleh titik (-3,-2)
Jika y = 5 maka x = -3 diperoleh titik (-3,5)
Langkah 2. Letakkan titik (-3,-2) dan (-3,5) pada bidang koordinat kartesius.
Langkah 3. Hubungkan titik (-3,-2) dan (-3,5) maka diperoleh grafik garis x = -3.

TIPS: garis x = h adalah garis yang sejajar dengan sumbu Y dan melalui titik (h,0).
Contoh 3
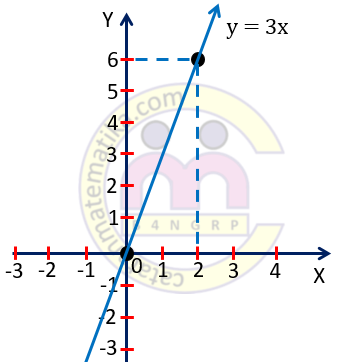
Gambarlah grafik persamaan garis lurus y = 3x
Penyelesaian:
Langkah 1. Tentukan dua titik sembarang
Jika x = 0 maka:
y = 3x
y = 3.0
y = 0
Diperoleh titik (0, 0)
Jika x = 2 maka:
y = 3x
y = 3.2
y = 6
diperoleh titik (2, 6)
Langkah 2. Letakkan titik (0,0) dan (2,6) pada bidang koordinat kartesius.
Langkah 3. Hubungkan titik (0,0) dan (2,6) maka diperoleh grafik garis y = 3x
Contoh 4
Gambarlah grafik persamaan garis $y = 3x – 5$
Penyelesaian:
Langkah 1. Tentukan dua titik sembarang
Jika x = 1 maka:
y = 3x – 5
y = 3.1 – 5
y = 3 – 5
y = -2
diperoleh titik (1, -2)
Jika x = 3 maka:
y = 3x – 5
y = 3.3 – 5
y = 9 – 5
y = 4
diperoleh titik (3, 4)
Langkah 2. Letakkan titik (1,-2) dan (3,4) pada bidang koordinat kartesius.
Langkah 3. Hubungkan titik (1,-2) dan (3,4) maka diperoleh grafik garis $y = 3x – 5$.

Contoh 5
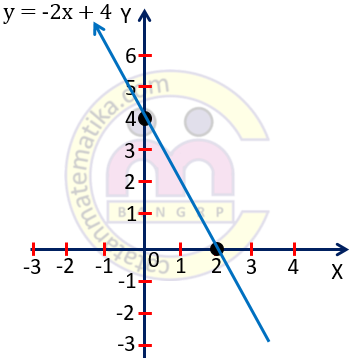
Gambarlah grafik persamaan garis $y = -2x + 4$
Penyelesaian:
Langkah 1. Tentukan dua titik sembarang
Dalam menentukan dua titik sembarang, kita juga dapat menggunakan titik potong terhadap sumbu X dan sumbu Y, sebagai berikut:
Titik potong terhadap sumbu X maka nilai y = 0
$\begin{align} y &= -2x + 4 \\ 0 &= -2x + 4 \\ 2x &=4 \\ x &= \frac{4}{2} \\ x &= 2 \end{align}$
diperoleh titik (2, 0)
Titik potong terhadap sumbu Y maka nilai x = 0
$\begin{align} y &= -2x + 4 \\ y &= -2.0 + 4 \\ y &= 4 \end{align}$
diperoleh titik (0, 4)
Langkah 2. Letakkan titik (2,0) dan (0,4) pada bidang koordinat kartesius.
Langkah 3. Hubungkan titik (2,0) dan (0,4) maka diperoleh grafik garis $y = -2x + 4$
Contoh 6
Gambarlah grafik persamaan garis $2x + 5y = 20$
Penyelesaian:
Langkah 1. Tentukan dua titik sembarang
Titik potong terhadap sumbu X, maka nilai y = 0
$\begin{align} 2x + 5y &=20 \\ 2x + 5.0 &= 20 \\ 2x &= 20 \\ x &= \frac{20}{2} \\ x &= 10 \end{align}$
diperoleh titik (10, 0)
Titik potong terhadap sumbu Y, maka nilai x = 0
$\begin{align} 2x + 5y &=20 \\ 2.0 + 5y &= 20 \\ 5y &= 20 \\ y &= \frac{20}{5} \\ y &= 4 \end{align}$
diperoleh titik (0, 4)
Langkah 2. Letakkan titik (10,0) dan (0,4) pada bidang koordinat kartesius.
Langkah 3. Hubungkan titik (10,0) dan (0,4) maka diperoleh grafik garis 2x + 5y = 20.

Contoh 7
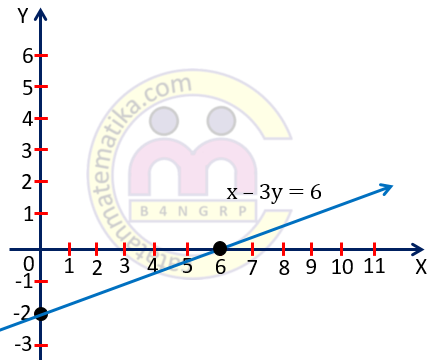
Gambarlah grafik persamaan garis x – 3y = 6
Penyelesaian:
Langkah 1. Tentukan dua titik sembarang
Titik potong terhadap sumbu X, maka nilai y = 0
$\begin{align} x – 3y &= 6 \\ x – 3.0 &= 6 \\ x &= 6 \end{align}$
Diperoleh titik (6, 0)
Titik potong terhadap sumbu Y, maka nilai x = 0
$\begin{align} x – 3y &= 6 \\ 0 – 3y &= 6 \\ –3y &= 6 \\ y &= \frac{6}{-3} \\ y &= -2 \end{align}$
Diperoleh titik (0, -2)
Langkah 2. Letakkan titik (6,0) dan (0,-2) pada bidang koordinat kartesius.
Langkah 3. Hubungkan titik (6,0) dan (0,-2) maka diperoleh grafik garis x – 3y = 6
Latihan
Gambarlah grafik persamaan garis lurus berikut:
a) y = -1
b) x = 3
c) y = -2x
d) 3x – 4y = 12
e) 5x + 2y + 20 = 0
f) 4x + y = 8

Post a Comment for "Menggambar Grafik Persamaan Garis Lurus"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.