Pembahasan UTUL UGM 2019 Matematika IPA Kode 924 (Saintek)
Berikut ini adalah Pembahasan Soal UTUL UGM 2019 Matematika Saintek dengan kode soal 924.
Jika kalian ingin Download Soal Asli UTUL UGM Setiap tahun silahkan lihat DISINI.
Matematika IPA UTUL UGM 2019 No. 1
Sebuah kotak memuat 6 bola merah dan 4 bola hitam. Tiga bola diambil satu per satu tanpa pengembalian. Jika bola ketiga terambil merah, maka banyaknya kemungkinannya adalah …(A) 234
(B) 243
(C) 324
(D) 342
(E) 432
Pembahasan:
Kemungkinan-kemungkinannya:
HHM = 4 x 3 x 6 = 72
HMM = 4 x 6 x 5 = 120
MHM = 6 x 4 x 5 = 120
MMM = 6 x 5 x 4 = 120
Total = 72 + 120 + 120 + 120 = 432
Jawaban: E
Matematika IPA UTUL UGM 2019 No. 2
Diketahui penyelesaian dari pertidaksamaan $\frac{{{3}^{x+3}}+{{3}^{x}}-36}{{{9}^{x}}-9}\le 3$ adalah $a\le x<b$ atau $x\ge c$. Nilai $a+2b+c$ = …(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Pembahasan:
$\frac{{{3}^{x+3}}+{{3}^{x}}-36}{{{9}^{x}}-9}\le 3$
$\frac{{{3}^{3}}{{.3}^{x}}+{{3}^{x}}-36}{{{\left( {{3}^{x}} \right)}^{2}}-9}-3\le 0$
$\frac{{{28.3}^{x}}-36}{{{\left( {{3}^{x}} \right)}^{2}}-9}-3\le 0$
Misal: ${{3}^{x}}=p$ , $p>0$ maka:
$\frac{28p-36}{{{p}^{2}}-9}-3\le 0$
$\frac{28p-36}{{{p}^{2}}-9}-\frac{3\left( {{p}^{2}}-9 \right)}{{{p}^{2}}-9}\le 0$
$\frac{-3{{p}^{2}}+28p-9}{{{p}^{2}}-9}\le 0$
$\frac{3{{p}^{2}}-28p+9}{{{p}^{2}}-9}\ge 0$
Cari p pembuat nol:
$3{{p}^{2}}-28p+9=0$
$(3p-1)(p-9)=0$
$p=\frac{1}{3}$ atau $p=9$
$p=\frac{1}{3}\to {{3}^{x}}={{3}^{-1}}\Leftrightarrow x=-1$
$p=9\to {{3}^{x}}={{3}^{2}}\Leftrightarrow x=2$
${{p}^{2}}-9\ne 0$
$(p+3)(p-3)\ne 0$
$p\ne -3$ atau $p\ne 3$
$p\ne 3\to {{3}^{x}}\ne 3\Leftrightarrow x\ne 1$
Uji garis bilangan:
$-1\le x < 1$ atau $x \ge 2$
$a \le x < b$ atau $x \ge c$
$a=-1$, $b=1$, $c=2$
$a+2b+c=-1+2.1+2=3$
Jawaban: D
Matematika IPA UTUL UGM 2019 No. 3
Jika $a < x < b$ adalah solusi pertidaksamaan $1+{{2}^{x}}+{{2}^{2x}}+{{2}^{3x}}+... > 2$, dengan $x \ne 1$ maka $a+b$ = …(A) $-1$
(B) $-2$
(C) $-3$
(D) $-4$
(E) $-5$
Pembahasan:
Barisan Geometri Tak Hingga:
$1+{{2}^{x}}+{{2}^{2x}}+{{2}^{3x}}+... > 2$
$a=1$, $r={{2}^{x}}$, ${{S}_{\infty }}=\frac{a}{1-r}$
$1+{{2}^{x}}+{{2}^{2x}}+{{2}^{3x}}+... > 2$
$\frac{1}{1-{{2}^{x}}} > 2$
$\frac{1}{1-{{2}^{x}}}-2 > 0$
$\frac{1}{1-{{2}^{x}}}-\frac{2\left( 1-{{2}^{x}} \right)}{1-{{2}^{x}}} > 0$
$\frac{{{2.2}^{x}}-1}{1-{{2}^{x}}} > 0$
$({{2.2}^{x}}-1)(1-{{2}^{x}}) > 0$
${{2.2}^{x}}-2.{{({{2}^{x}})}^{2}}-1+{{2}^{x}} > 0$
$2.{{({{2}^{x}})}^{2}}-{{3.2}^{x}}+1 < 0$
$({{2.2}^{x}}-1)({{2}^{x}}-1) < 0$
${{2}^{x}}=\frac{1}{2}$ ; ${{2}^{x}}=1$
$\frac{1}{2}<{{2}^{x}} < 1$
${{2}^{-1}}<{{2}^{x}} < {{2}^{0}}$
$-1 < x < 0\equiv a < x < b$
maka $a=-1$ dan $b=0$
$a+b=-1+0=-1$
Jawaban: A
Matematika IPA UTUL UGM 2019 No. 4
Diberikan lingkaran pada bidang koordinat dengan titik pusat $(a,b)$ dan memotong sumbu-X di titik $(3,0)$ dan $(9,0)$. Jika garis yang melalui titik $(0,3)$ menyinggung lingkaran di titik $(3,0)$, maka nilai dari ${{a}^{2}}-{{b}^{2}}$ adalah …(A) 9
(B) 18
(C) 27
(D) 36
(E) 45
Pembahasan:
Persamaan lingkaran dengan pusat (a,b):
${{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}}$
Memotong sumbu X di titik (3,0) dan (9,0) maka:
$\begin{align}{{(3-a)}^{2}}+{{(0-b)}^{2}} &={{r}^{2}} \\ 9-6a+{{a}^{2}}+{{b}^{2}} &={{r}^{2}} \\ {{a}^{2}}+{{b}^{2}}-6a-{{r}^{2}} &=-9\,...\,(1) \end{align}$
$\begin{align}{{(9-a)}^{2}}+{{(0-b)}^{2}} &={{r}^{2}} \\ 81-18a+{{a}^{2}}+{{b}^{2}} &={{r}^{2}} \\ {{a}^{2}}+{{b}^{2}}-18a-{{r}^{2}} &=-81\,...\,(2) \end{align}$
Pers (1) dikurang pers (2) maka:
$\begin{align}{{a}^{2}}+{{b}^{2}}-6a-{{r}^{2}} &=-9 \\ {{a}^{2}}+{{b}^{2}}-18a-{{r}^{2}} &=-81 \end{align}$
----------------------------- (-)
$12a=72\Leftrightarrow a=6$
Garis yang melalui titik (0,3) menyinggung lingkaran di (3,0) maka:
Garis melalui titik (0,3) dan (3,0) tegak lurus dengan garis yang melalui titik pusat (6,b) dan (3,0) maka:
$\begin{align}{{m}_{1}}.{{m}_{2}} &=-1 \\ \frac{0-3}{3-0}.\frac{0-b}{3-6} &=-1 \\ -1.\frac{-b}{-3} &=-1 \\ b &=3 \end{align}$
${{a}^{2}}-{{b}^{2}}={{6}^{2}}-{{3}^{2}}=27$
Jawaban: C
Matematika IPA UTUL UGM 2019 No. 5
Jika ${{(x-2)}^{2}}$ membagi ${{x}^{4}}-a{{x}^{3}}+b{{x}^{2}}+4x-4$, maka $ab$ = …(A) 9
(B) 12
(C) 16
(D) 20
(E) 25
Pembahasan:
${{x}^{4}}-a{{x}^{3}}+b{{x}^{2}}+4x-4$ = ${{(x-2)}^{2}}P(x)$
${{x}^{4}}-a{{x}^{3}}+b{{x}^{2}}+4x-4$ = $({{x}^{2}}-4x+4)P(x)$
Dengan memperhatikan koefisien ${{x}^{4}}$ dan konstanta maka:
${{x}^{4}}-a{{x}^{3}}+b{{x}^{2}}+4x-4$ = $({{x}^{2}}-4x+4)({{x}^{2}}+mx-1)$
${{x}^{4}}-a{{x}^{3}}+b{{x}^{2}}+4x-4$ = ${{x}^{4}}+(m-4){{x}^{3}}+(3-4m){{x}^{2}}+(4+4m)x-4$
Perhatikan koefisien $x$:
$4+4m=4\Leftrightarrow m=0$
Perhatikan koefisien ${{x}^{2}}$:
$b=3-4m\Leftrightarrow b=3-4.0\Leftrightarrow b=3$
Perhatikan koefisien ${{x}^{3}}$:
$-a=m-4\Leftrightarrow -a=0-4\Leftrightarrow a=4$
$a=4$, $b=3$ maka $ab=4.3=12$
Jawaban: B
Matematika IPA UTUL UGM 2019 No. 6
Diberikan empat matriks A, B, C, D berukuran $2\times 2$ dengan $A+C{{B}^{T}}=CD$. Jika A mempunyai invers, $\det ({{D}^{T}}-B)=m$ dan $\det (C)=n$ maka $\det (2{{A}^{-1}})$ = …(A) $\frac{4}{mn}$
(B) $\frac{mn}{4}$
(C) $\frac{4m}{n}$
(D) $4mn$
(E) $\frac{m+n}{4}$
Pembahasan:
Misalkan: $B=\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)$, dan $D=\left( \begin{matrix} p & q \\ r & s \\ \end{matrix} \right)$
$\begin{align}{{D}^{T}}-B &=\left( \begin{matrix} p & r \\ q & s \\ \end{matrix} \right)-\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right) \\ &=\left( \begin{matrix} p-a & r-b \\ q-c & s-d \\ \end{matrix} \right) \end{align}$
$\begin{align} D-{{B}^{T}} &= \left( \begin{matrix} p & q \\ r & s \\ \end{matrix} \right)-\left( \begin{matrix} a & c \\ b & d \\ \end{matrix} \right) \\ &= \left( \begin{matrix} p-a & q-c \\ r-b & s-d \\ \end{matrix} \right) \end{align}$
Perhatikan, ternyata:
$\det (D-{{B}^{T}})=\det ({{D}^{T}}-B)$
$A+C{{B}^{T}}=CD$
$A=CD-C{{B}^{T}}$
$A=C(D-{{B}^{T}})$
$|A|=|C||(D-{{B}^{T}})|$
$|A|=|C||({{D}^{T}}-B)|$
$|A|=n.m$
$\det (2{{A}^{-1}})={{2}^{2}}.\frac{1}{|A|}=\frac{4}{mn}$
Jawaban: A
Matematika IPA UTUL UGM 2019 No. 7
Jika $-\frac{\pi }{2} < x < \frac{\pi }{2}$ dan $x$ memenuhi $5{{\cos }^{2}}x+3\sin x \cos x \ge 1$ maka himpunan semua $y=\tan x$ adalah …(A) $\{y \in R:-1\le y \le 4\}$
(B) $\{y \in R:-4\le y \le 1\}$
(C) $\{y \in R:-4\le y \le -1\}$
(D) $\{y \in R:1\le y \le 4\}$
(E) $\mathbb{R}$
Pembahasan:
$5{{\cos }^{2}}x+3\sin x\cos x \ge 1$
$5{{\cos }^{2}}x+3\sin x\cos x-1 \ge 0$
$\frac{5{{\cos }^{2}}x}{{{\cos }^{2}}x}+\frac{3\sin x\cos x}{{{\cos }^{2}}x}-\frac{1}{{{\cos }^{2}}x} \ge 0$
$5+3\tan x-{{\sec }^{2}}x \ge 0$
$4+3\tan x+1-{{\sec }^{2}}x \ge 0$
$4+3\tan x-{{\tan }^{2}}x \ge 0$
Karena $y=\tan x$ maka:
$4+3y-{{y}^{2}} \ge 0$
${{y}^{2}}-3y-4 \le 0$
$(y+1)(y-4) \le 0$
$-1\le y \le 4$
Jawaban: A
Matematika IPA UTUL UGM 2019 No. 8
Jika suku banyak ${{x}^{4}}+3{{x}^{3}}+A{{x}^{2}}+5x+B$ dibagi ${{x}^{2}}+2x+2$ bersisa $7x+14$, maka jika dibagi ${{x}^{2}}+4x+4$ akan bersisa …(A) $x+1$
(B) $x+2$
(C) $x+3$
(D) $2x+1$
(E) $2x+4$
Pembahasan:
Yang dibagi = pembagi x hasil + sisa
${{x}^{4}}+3{{x}^{3}}+A{{x}^{2}}+5x+B$ = $({{x}^{2}}+2x+2)({{x}^{2}}+mx+n)$ + $7x+14$
${{x}^{4}}+3{{x}^{3}}+A{{x}^{2}}+5x+B$ = ${{x}^{4}}+(m+2){{x}^{3}}+(n+2m+2){{x}^{2}}+(2n+2m+7)x+2n+14$
${{x}^{4}}+3{{x}^{3}}+A{{x}^{2}}+5x+B$ = $({{x}^{2}}+2x+2)({{x}^{2}}+x-2)$ + $7x+14$
${{x}^{4}}+3{{x}^{2}}+A{{x}^{2}}+5x+B$ = ${{x}^{4}}+3{{x}^{3}}+2{{x}^{2}}-2x-4$ + $7x+14$
${{x}^{4}}+3{{x}^{2}}+A{{x}^{2}}+5x+B$ = ${{x}^{4}}+3{{x}^{3}}+2{{x}^{2}}+5x+10$
${{x}^{4}}+3{{x}^{3}}+A{{x}^{2}}+5x+B$ dibagi ${{x}^{2}}+4x+4$ sama dengan:
$({{x}^{4}}+3{{x}^{3}}+2{{x}^{2}}+5x+10)$ : $(x+2)(x+2)$ maka sisa?
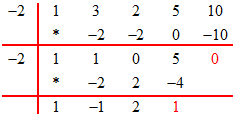
${{S}_{1}}=0$ dan ${{S}_{2}}=1$
$\begin{align} S(x) &={{S}_{2}}(x+2)+{{S}_{1}} \\ &=1(x+2)+0 \\ S(x) &=x+2 \end{align}$
Jawaban: B
Matematika IPA UTUL UGM 2019 No. 9
Jika ${{\left( ^{2}\log x \right)}^{2}}-{{\left( ^{2}\log y \right)}^{2}}{{=}^{2}}\log 256$ dan $^{2}\log {{x}^{2}}{{-}^{2}}\log {{y}^{2}}{{=}^{2}}\log 16$, maka nilai dari $^{2}\log {{x}^{6}}{{y}^{-2}}$ adalah …(A) 24
(B) 20
(C) 16
(D) 8
(E) 4
Pembahasan:
$^{2}\log {{x}^{2}}{{-}^{2}}\log {{y}^{2}}{{=}^{2}}\log 16$
${{2.}^{2}}\log x-{{2.}^{2}}\log y=4$
$^{2}\log x{{-}^{2}}\log y=2$
${{\left( ^{2}\log x \right)}^{2}}-{{\left( ^{2}\log y \right)}^{2}}{{=}^{2}}\log 256$
${{(}^{2}}\log x{{+}^{2}}\log y){{(}^{2}}\log x{{-}^{2}}\log y){{=}^{2}}\log {{2}^{8}}$
${{(}^{2}}\log x{{+}^{2}}\log y).2=8$
$^{2}\log x{{+}^{2}}\log y=4$
$^{2}\log x{{-}^{2}}\log y=2$
---------------------- (-)
${{2.}^{2}}\log y=2$
$^{2}\log y=1\Leftrightarrow y=2$
$^{2}\log x{{-}^{2}}\log y=2$
$^{2}\log x-1=2$
$^{2}\log x=3\Leftrightarrow x={{2}^{3}}$
$\begin{align} ^{2}\log {{x}^{6}}{{y}^{-2}} &{{=}^{2}}\log {{({{2}^{3}})}^{6}}{{.2}^{-2}} \\ & {{=}^{2}}\log {{2}^{18}}{{.2}^{-2}} \\ & {{=}^{2}}\log {{2}^{16}} \\ ^{2}\log {{x}^{6}}{{y}^{-2}} &=16 \end{align}$
Jawaban: C
Matematika IPA UTUL UGM 2019 No. 10
Diberikan kubus ABCD.EFGH dan P adalah titik tengah BC. Perbandingan luas segitiga APG dan luas DPG adalah …(A) 1 : 1
(B) $\sqrt{3}:\sqrt{2}$
(C) $\sqrt{2}:1$
(D) 3 : 2
(E) $\sqrt{3}:1$
Pembahasan:
Perhatikan gambar berikut ini!
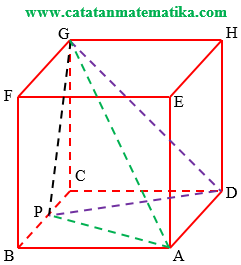
Misalkan panjang rusuk kubus 2 cm, maka BP = PC = 1 cm
Perhatikan $\Delta APG$
$\begin{align}AP &=\sqrt{A{{B}^{2}}+B{{P}^{2}}} \\ &=\sqrt{{{2}^{2}}+{{1}^{2}}} \\ AP &=\sqrt{5} \end{align}$
$\begin{align}PG &=\sqrt{P{{C}^{2}}+C{{G}^{2}}} \\ & =\sqrt{{{1}^{2}}+{{2}^{2}}} \\ PG &=\sqrt{5} \end{align}$
AG = diagonal ruang kubus maka $AG=2\sqrt{3}$.
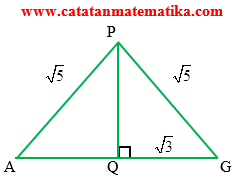
$\begin{align}PQ &=\sqrt{P{{G}^{2}}-Q{{G}^{2}}} \\ & =\sqrt{{{(\sqrt{5})}^{2}}-{{(\sqrt{3})}^{2}}} \\ PQ &=\sqrt{2} \end{align}$
$\begin{align} L.\Delta APG &=\frac{1}{2}.AG.PQ \\ & =\frac{1}{2}.2\sqrt{3}.\sqrt{2} \\ L.\Delta APG &=\sqrt{6} \end{align}$
Perhatikan $\Delta DPG$
$\begin{align} DP &=\sqrt{P{{C}^{2}}+C{{D}^{2}}} \\ & =\sqrt{{{1}^{2}}+{{2}^{2}}} \\ DP &=\sqrt{5} \end{align}$
GD = diagonal sisi kubus maka $DG=2\sqrt{2}$
$\begin{align}PR &=\sqrt{P{{G}^{2}}-R{{G}^{2}}} \\ &=\sqrt{{{(\sqrt{5})}^{2}}-{{(\sqrt{2})}^{2}}} \\ PR &=\sqrt{3} \end{align}$
$\begin{align}L.\Delta DPG &=\frac{1}{2}.DG.PR \\ &=\frac{1}{2}.2\sqrt{2}.\sqrt{3} \\ L.\Delta DPG &=\sqrt{6} \end{align}$
$L.\Delta APG:L.\Delta DPG=\sqrt{6}:\sqrt{6}=1:1$
Jawaban: A
Matematika IPA UTUL UGM 2019 No. 11
Misalkan ${{U}_{n}}$ menyatakan suku ke-$n$ dari barisan aritmetika. Diketahui ${{U}_{1}}\times {{U}_{2}}=10$ dan ${{U}_{1}}\times {{U}_{3}}=16$. Jika suku-suku dari barisan aritmetika tersebut merupakan bilangan positif, maka ${{U}_{10}}$ = …(A) 21
(B) 23
(C) 25
(D) 27
(E) 29
Pembahasan:
${{U}_{1}}\times {{U}_{2}}=10=2.5$
${{U}_{1}}\times {{U}_{3}}=16=2.8$
Barisan aritmetika:
2, 5, 8
$a=2$, $b=3$
$\begin{align}{{U}_{10}} &=a+9b \\ &=2+9.3 \\ {{U}_{10}} &=29 \end{align}$
Jawaban: E
Matematika IPA UTUL UGM 2019 No. 12
Diketahui fungsi $f$ dan $g$ dengan $f(x)={{\left( 2x+1 \right)}^{5}}$ dan $h=f\circ g$. Jika $g(5)=-1$ dan $g'\left( \frac{x+1}{x-1} \right)=2x+2$, maka $h'(5)$ = …(A) 10
(B) 25
(C) 50
(D) 60
(E) 120
Pembahasan:
$f(x)={{\left( 2x+1 \right)}^{5}}$
$f'(x)=5{{\left( 2x+1 \right)}^{5-1}}.2$
$f'(x)=10{{\left( 2x+1 \right)}^{4}}$
$g'\left( \frac{x+1}{x-1} \right)=2x+2$
$\begin{align}\frac{x+1}{x-1} &=5 \\ 5x-5 &=x+1 \\ 4x &=6 \\ x &=\frac{3}{2} \end{align}$
$g'\left( \frac{x+1}{x-1} \right)=2x+2$
$g'\left( 5 \right)=2.\frac{3}{2}+2\Leftrightarrow g'(5)=5$
$h=f\circ g$
$h(x)=f(g(x))$
$h'(x)=g'(x).f'(g(x))$
$h'(5)=g'(5).f'(g(5))$
$\begin{align}h'(5) &=g'(5).f'(g(5)) \\ & =5.f'(-1) \\ & =5.10{{[2(-1)+1]}^{2}} \\ & =50 \end{align}$
Jawaban: C
Matematika IPA UTUL UGM 2019 No. 13
Jika $p>0$ dan $\underset{x\to p}{\mathop{\lim }}\,\frac{{{x}^{3}}+p{{x}^{2}}+qx}{x-p}=12$, maka nilai $p-q$ adalah …(A) 14
(B) 10
(C) 8
(D) 5
(E) 3
Pembahasan:
Untuk $x=p$ maka:
${{x}^{3}}+p{{x}^{2}}+qx=0$
${{p}^{3}}+p.{{p}^{2}}+q.p=0$
$2{{p}^{3}}+pq=0$
$2{{p}^{2}}+q=0$
Dalil L’Hospital:
$\begin{align} \underset{x\to p}{\mathop{\lim }}\,\frac{{{x}^{3}}+p{{x}^{2}}+qx}{x-p} &=12 \\ \underset{x\to p}{\mathop{\lim }}\,\frac{3{{x}^{2}}+2px+q}{1} &=12 \\ 3.{{p}^{2}}+2p.p+q &=12 \\ 3{{p}^{2}}+2{{p}^{2}}+q &=12 \\ 3{{p}^{2}}+0 &=12 \\ {{p}^{2}} &=4 \\ p &=\pm 2 \end{align}$
Karena $p>0$ maka $p=2$ substitusi ke:
$\begin{align}2{{p}^{2}}+q &=0 \\ {{2.2}^{2}}+q &=0 \\ q &=-8 \end{align}$
$p-q=2-(-8)=10$
Jawaban: B
Matematika IPA UTUL UGM 2019 No. 14
Jika $\sin x+\sin 2x+\sin 3x=0$ untuk $\frac{\pi }{2}<x<\pi $, maka $\tan 2x$ = …(A) $-\sqrt{3}$
(B) $-1$
(C) $-\frac{1}{3}\sqrt{3}$
(D) $\frac{1}{3}\sqrt{3}$
(E) $\sqrt{3}$
Pembahasan:
$\sin x+\sin 2x+\sin 3x=0$
$\sin 3x+\sin x+\sin 2x=0$
$2\sin \left( \frac{3x+x}{2} \right)\cos \left( \frac{3x-x}{2} \right)+\sin 2x=0$
$2\sin 2x.\cos x+\sin 2x=0$
$\sin 2x(2\cos x+1)=0$
$2\cos x+1=0$
$\cos x=-\frac{1}{2}$
$\sin x=\frac{1}{2}\sqrt{3}$
$\tan x=-\sqrt{3}$
$\begin{align} \tan 2x &=\frac{2\tan x}{1-{{\tan }^{2}}x} \\ & =\frac{2(-\sqrt{3})}{1-{{(-\sqrt{3})}^{2}}} \\ & =\frac{-2\sqrt{3}}{1-3} \\ & =\frac{-2\sqrt{3}}{-2} \\ \tan 2x &=\sqrt{3} \end{align}$
Jawaban: E
Matematika IPA UTUL UGM 2019 No. 15
Diketahui ${{x}^{2}}+2xy+4x=-3$ dan $9{{y}^{2}}+4xy+12y=-1$. Nilai dari $x+3y$ adalah …(A) 2
(B) 1
(C) 0
(D) $-1$
(E) $-2$
Pembahasan:
${{x}^{2}}+2xy+4x=-3$
$9{{y}^{2}}+4xy+12y=-1$
------------------------- (+)
${{x}^{2}}+9{{y}^{2}}+6xy+4x+12y=-4$
$({{x}^{2}}+6xy+9{{y}^{2}})+(4x+12y)=-4$
${{(x+3y)}^{2}}+4(x+3y)+4=0$
Misal: $x+3y=p$
${{p}^{2}}+4p+4=0$
$(p+2)(p+2)=0$
$p=-2$
$x+3y=p=-2$
Jawaban: E
Artikel Terkait: |
Semoga postingan: Pembahasan UTUL UGM 2019 Matematika IPA Kode 924 (Saintek) ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Pembahasan UTUL UGM 2019 Matematika IPA Kode 924 (Saintek)"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.