Home / Trigonometri

Soal Perbandingan Trigonometri Sudut Istimewa dan Pembahasan

Berikut ini adalah Soal dan Pembahasan Sudut-sudut Istimewa yaitu salah satu sub materi dari TRIGONOMETRI pada bidang studi Matematika.

Soal No. 1

$\sin 60^\circ .\cos 30^\circ +\cos 60^\circ .\sin 30^\circ $ = …
A. 1
B. $\frac{1}{2}$
C. $\frac{1}{2}\sqrt{2}$
D. $\frac{1}{2}$
E. 0

Penyelesaian: Lihat/Tutup

$\sin 60^\circ .\cos 30^\circ +\cos 60^\circ .\sin 30^\circ $
= $\frac{1}{2}\sqrt{3}.\frac{1}{2}\sqrt{3}+\frac{1}{2}.\frac{1}{2}$
= $\frac{3}{4}+\frac{1}{4}$
= 1
Jawaban: A

Soal No. 2

$\cos 60^\circ .\cos 30^\circ -\sin 60^\circ .\sin 30^\circ $ = ….
A. 0
B. $\frac{1}{2}$
C. $\frac{1}{2}\sqrt{2}$
D. $\frac{1}{2}\sqrt{3}$
E. $\sqrt{3}$

Penyelesaian: Lihat/Tutup

$\cos 60^\circ .\cos 30^\circ -\sin 60^\circ .\sin 30^\circ $
= $\frac{1}{2}.\frac{1}{2}\sqrt{3}-\frac{1}{2}\sqrt{3}.\frac{1}{2}$
= $\frac{1}{4}\sqrt{3}-\frac{1}{4}\sqrt{3}$
= 0
Jawaban: A

Soal No. 3

$\frac{{{\tan }^2}30^\circ .{{\sin }^2}60^\circ +{{\tan }^2}60^\circ .{{\cos }^2}30^\circ }{\sin 30^\circ .\cos 60^\circ }$= ….
A. 10
B. 5
C. 3
D. 2
E. 1

Penyelesaian: Lihat/Tutup

$\frac{{{\tan }^2}30^\circ .{{\sin }^2}60^\circ +{{\tan }^2}60^\circ .{{\cos }^2}30^\circ }{\sin 30^\circ .\cos 60^\circ }$
= $\frac{{{\left( \frac{1}{3}\sqrt{3} \right)}^2}{{\left( \frac{1}{2}\sqrt{3} \right)}^2}+{{\left( \sqrt{3} \right)}^2}{{\left( \frac{1}{2}\sqrt{3} \right)}^2}}{\frac{1}{2}.\frac{1}{2}}$
= $\frac{\frac{1}{3}.\frac{3}{4}+3.\frac{3}{4}}{\frac{1}{4}}$
= $\frac{\frac{1}{4}+\frac{9}{4}}{\frac{1}{4}}$
= $\frac{\frac{10}{4}}{\frac{1}{4}}$ = 10
Jawaban: A

Soal No. 4

Jika $n.\tan 45^\circ .\cos 60^\circ =\sin 60^\circ .\cot 60^\circ $, maka nilai $n$ adalah …
A. $\frac{1}{2}$
B. 1
C. $\frac{1}{\sqrt{2}}$
D. $\frac{1}{\sqrt{3}}$
E. $\sqrt{3}$

Penyelesaian: Lihat/Tutup

$\begin{align} n.\tan 45^\circ .\cos 60^\circ &=\sin 60^\circ .\cot 60^\circ \\ n.1.\frac{1}{2} &=\frac{1}{2}\sqrt{3}.\frac{1}{\tan 60^\circ } \\ n &=\sqrt{3}.\frac{1}{\sqrt{3}} \\ n &=1 \end{align}$
Jawaban: B

Soal No. 5

Pada sebuah segitiga siku-siku ABC dimana $\cos A.\cos B=\frac{1}{8}$ berlaku bahwa: $\cos A.\cos B.\cos C$ = …
A. $-1$
B. 0
C. $\frac{1}{7}$
D. $\frac{1}{8}$
E. $\frac{1}{4}$

Penyelesaian: Lihat/Tutup

$\cos A.\cos B=\frac{1}{8}$ dari persamaan ini kita peroleh bahwa: $\angle A,\angle B\ne 90^\circ $, karena segitiga ABC adalah segitiga siku-siku maka $\angle C=90^\circ $.
$\begin{align} \cos A.\cos B.\cos C &=\frac{1}{8}.\cos 90^\circ \\ &=\frac{1}{8}.0 \\ \cos A.\cos B.\cos C &=0 \end{align}$
Jawaban: B

Soal No. 6

Nilai dari $\left( {{\sin }^2}\frac{\pi }{6}+{{\sin }^{4}}\frac{\pi }{3}+{{\cos }^2}\frac{\pi }{2}-{{\cos }^2}\frac{\pi }{6} \right)$ adalah ….
A. $\frac{1}{16}$
B. $\frac{3}{16}$
C. $\frac{9}{16}$
D. $\frac{11}{16}$
E. $\frac{13}{16}$

Penyelesaian: Lihat/Tutup

${{\sin }^2}\frac{\pi }{6}+{{\sin }^{4}}\frac{\pi }{3}+{{\cos }^2}\frac{\pi }{2}-{{\cos }^2}\frac{\pi }{6}$
= ${{(\sin 30^\circ )}^2}+{{(\sin 60^\circ )}^{4}}+{{(\cos 90^\circ )}^2}-{{(\cos 30^\circ )}^2}$
= ${{\left( \frac{1}{2} \right)}^2}+{{\left( \frac{1}{2}\sqrt{3} \right)}^{4}}+{{0}^2}-{{\left( \frac{1}{2}\sqrt{3} \right)}^2}$
= $\frac{1}{4}+\frac{9}{16}-\frac{3}{4}$
= $\frac{4+9-12}{16}=\frac{1}{16}$
Jawaban: A

Soal No. 7

Jika ${{\tan }^2}{{45}^{\circ }}-{{\cos }^2}{{30}^{\circ }}=x.\sin {{45}^{\circ }}.\cos {{45}^{\circ }}$ maka nilai $x$ adalah ….
A. $-2$
B. $-\frac{1}{2}$
C. $-\frac{1}{3}$
D. $\frac{1}{2}$
E. 2

Penyelesaian: Lihat/Tutup

$\begin{align} {{\tan }^2}45^\circ -{{\cos }^2}30^\circ &=x.\sin 45^\circ .\cos 45^\circ \\ {{1}^2}-{{\left( \frac{1}{2}\sqrt{3} \right)}^2} &=x.\frac{1}{2}\sqrt{2}.\frac{1}{2}\sqrt{2} \\ 1-\frac{3}{4} &=\frac{1}{2}x \\ \frac{1}{4} &=\frac{1}{2}x \\ \frac{2}{4}= &x=\frac{1}{2} \end{align}$
Jawaban: D

Soal No. 8

$\frac{\cos 45^\circ .\cos 30^\circ +\sin 45^\circ .\sin 60^\circ }{\tan 30^\circ .\tan 60^\circ }$ senilai dengan ….
A. $\frac{1}{4}\sqrt{3}$
B. $\frac{1}{2}\sqrt{6}$
C. 1
D. $\frac{3}{2}\sqrt{2}$
E. 2

Penyelesaian: Lihat/Tutup

$\frac{\cos 45^\circ .\cos 30^\circ +\sin 45^\circ .\sin 60^\circ }{\tan 30^\circ .\tan 60^\circ }$
= $\frac{\frac{1}{2}\sqrt{2}.\frac{1}{2}\sqrt{3}+\frac{1}{2}\sqrt{2}.\frac{1}{2}\sqrt{3}}{\frac{1}{3}\sqrt{3}.\sqrt{3}}$
= $\frac{\frac{1}{4}\sqrt{2}+\frac{1}{4}\sqrt{2}}{\frac{1}{3}\sqrt{3}}$
= $\frac{\frac{1}{2}\sqrt{2}}{\frac{1}{3}\sqrt{3}}$
= $\frac{3\sqrt{2}}{2\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $\frac{1}{2}\sqrt{6}$
Jawaban: B

Soal No. 9

Nilai dari $\sin 30^\circ +\cos 60^\circ $ = …
A. $\frac{1}{2}\sqrt{3}$
B. $\frac{1}{2}\sqrt{2}$
C. 1
D. $-\frac{1}{2}\sqrt{2}$
E. $-\frac{1}{2}\sqrt{3}$

Penyelesaian: Lihat/Tutup

$\sin 30^\circ +\cos 60^\circ =\frac{1}{2}+\frac{1}{2}=1$
Jawaban: C

Soal No. 10 (Soal HOTS)

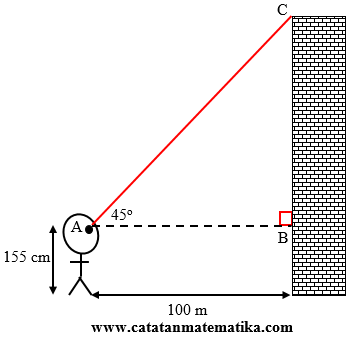
Tomy berdiri 100 m dari dinding gedung bertingkat, ia melihat ke puncak gedung tersebut dengan sudut elevasi $45^\circ $. Jika tinggi Tomy (dari kaki sampai mata) adalah 155 cm, maka tinggi gedung adalah ….
A. 225 m
B. 101,55 m
C. 101 m
D. $100\sqrt{2}$ m
E. $50\sqrt{2}$ m

Penyelesaian: Lihat/Tutup

Perhatikan sketsa gambar berikut!
Soal Sudut-sudut Istimewa dan Pembahasan

Soal Sudut-sudut Istimewa dan Pembahasan

Pada segitiga ABC:
AB = 100 m
$\begin{align} \tan A &=\frac{BC}{AB} \\ \tan 45^\circ &=\frac{BC}{100} \\ 1 &=\frac{BC}{100} \\ BC &=100 \end{align}$
Tinggi gedung
= 155 cm + BC
= 1,55 m + 100 m
= 101,55 m
Jawaban: B

Soal No. 11 (Soal HOTS)

Soal HOTS. Sebuah benda membentuk bayangan di tanah dengan panjang 90 cm ketika sudut elevasi sinar matahari $30^\circ $ (sudut kemiringan sinar matahari terhadap horizontal). Tinggi benda tersebut adalah … cm.
A. $90\sqrt{3}$
B. $30\sqrt{3}$
C. 45
D. $45\sqrt{2}$
E. 60

Penyelesaian: Lihat/Tutup

Perhatikan sketsa gambar berikut!
Soal HOTS Sudut-sudut Istimewa dan Pembahasan

Soal HOTS Sudut-sudut Istimewa dan Pembahasan

Tinggi benda = BC
$\begin{align} \tan A &=\frac{BC}{AB} \\ \tan 30^\circ &=\frac{BC}{90} \\ \frac{\sqrt{3}}{3} &=\frac{BC}{90} \\ 3BC &=90\sqrt{3} \\ BC &=30\sqrt{3} \end{align}$
Jadi, tinggi benda tersebut adalah $30\sqrt{3}$ cm.
Jawaban: B

Soal No. 12 (Soal HOTS)

Seorang berjalan lurus di jalan yang datar ke arah cerobong asap. Dari lokasi A, ujung cerobong itu terlihat dengan sudut elevasi $45^\circ $, kemudian ia berjalan lurus sejauh 10 m ke lokasi B. Dari lokasi B, cerobong asap terlihat dengan sudut elevasi $60^\circ $. Jika tinggi orang itu 1,6 m, maka tinggi cerobong asap adalah … meter.
A. 15 + $5\sqrt{3}$
B. 15 + $3\sqrt{5}$
C. 16,6 + $5\sqrt{3}$
D. 16,6 + $3\sqrt{5}$
E. 16,6 + $5\sqrt{2}$

Penyelesaian: Lihat/Tutup

Perhatikan gambar berikut!
Soal Hots Sudut-sudut Istimewa dan Pembahasan

Soal Hots Sudut-sudut Istimewa dan Pembahasan

Perhatikan segitiga ADC:
$\begin{align} \tan A &=\frac{CD}{AD} \\ \tan 45^\circ &=\frac{CD}{AB+BD} \\ 1 &=\frac{CD}{10+BD} \\ 10+BD &=CD \\ BD &=CD-10 \end{align}$
Perhatikan segitiga BDC:
$\begin{align} \tan B &=\frac{CD}{BD} \\ \tan 60^\circ &=\frac{CD}{BD} \\ \sqrt{3} &=\frac{CD}{BD} \\ BD &=\frac{CD}{\sqrt{3}} \\ CD-10 &=\frac{CD}{\sqrt{3}} \\ \sqrt{3}.CD-10\sqrt{3} &=CD \\ (\sqrt{3}-1)CD &=10\sqrt{3} \\ CD &=\frac{10\sqrt{3}}{\sqrt{3}-1}\times \frac{\sqrt{3}+1}{\sqrt{3}+1} \\ CD &=\frac{30+10\sqrt{3}}{3-1} \\ CD &=15+5\sqrt{3} \end{align}$
Tinggi cerobong asap:
= CD + 1,6 m
= 15 + $5\sqrt{3}$ + 1,6
= 16,6 + $5\sqrt{3}$
Jawaban: C

Soal No. 13 (Soal HOTS)

Seorang anak berdiri di suatu tempat A di tepi sungai yang lurus. Ia mengamati dua pohon B dan C yang berada di seberang sungai. Pohon B tepat di seberang A. Jarak pohon B dan C adalah $2\sqrt{3}$ meter dan besar sudut BAC = $30^\circ $, lebar sungai adalah … meter.
A. 2
B. 3
C. 6
D. $6\sqrt{2}$
E. $6\sqrt{3}$

Penyelesaian: Lihat/Tutup

Perhatikan gambar berikut!
Soal Hots Sudut-sudut Istimewa dan Pembahasan

Soal Hots Sudut-sudut Istimewa dan Pembahasan

Perhatikan segitiga BAC:
$\begin{align} \tan A &=\frac{BC}{AB} \\ \tan 30^\circ &=\frac{2\sqrt{3}}{AB} \\ \frac{1}{\sqrt{3}} &=\frac{2\sqrt{3}}{AB} \\ AB &=6 \end{align}$
Jadi, lebar sungai = AB = 6 meter.
Jawaban: C

Soal No. 14 (Soal HOTS)

Panjang benang layang-layang adalah 150 m dan sudut elevasi layang-layang terhadap tanah adalah $60^\circ $. Tinggi layang-layang terhadap tanah adalah … meter.
A. $\frac{75}{2}\sqrt{2}$
B. $\frac{75}{2}\sqrt{3}$
C. 75
D. $75\sqrt{2}$
E. $75\sqrt{3}$

Penyelesaian: Lihat/Tutup

Perhatikan gambar berikut!
Soal Hots Sudut-sudut Istimewa dan Pembahasan

Soal Hots Sudut-sudut Istimewa dan Pembahasan

Perhatikan segitiga ABC:
$\begin{align} \sin A &=\frac{BC}{AC} \\ \sin 60^\circ &=\frac{BC}{150} \\ \frac{\sqrt{3}}{2} &=\frac{BC}{150} \\ BC &=75\sqrt{3} \end{align}$
Jadi, tinggi layang-layang terhadap tanah adalah $75\sqrt{3}$ meter.
Jawaban: E

Soal No. 15 (Soal HOTS)

Sebuah pesawat terbang berada pada ketinggian 1,8 km akan melakukan manuver dengan menanjak membentuk sudut $30^\circ $. Lama waktu yang diperlukan pesawat agar ketinggiannya 5 km, bila kecepatan pesawat tetap 320 km/jam adalah … detik.
A. 9
B. 18
C. 36
D. 72
E. 144

Penyelesaian: Lihat/Tutup

Perhatikan gambar berikut!
Soal Hots Sudut-sudut Istimewa dan Pembahasan

Soal Hots Sudut-sudut Istimewa dan Pembahasan

AD = BE = 1,8 km
EC = BC – BE = 5 – 1,8 = 3,2 km
Perhatikan segitiga DEC:
$\begin{align} \sin D &=\frac{CE}{DC} \\ \sin 30^\circ &=\frac{3,2}{DC} \\ \frac{1}{2} &=\frac{3,2}{DC} \\ DC &=6,4 \end{align}$
DC = jarak tempuh pesawat = 6,4 dan v = 320 km/jam maka:
$\begin{align} t &=\frac{\text{jarak}}{\text{kecepatan}} \\ & =\frac{6,4}{320}\text{jam} \\ & =\frac{64}{3200}\text{jam} \\ & =\frac{1}{50}\,\text{jam} \\ & =\frac{1}{50}\times 3600\,\text{detik} \\ t &=72\,\text{detik} \end{align}$
Jawaban: D

Soal No. 16 (Soal HOTS)

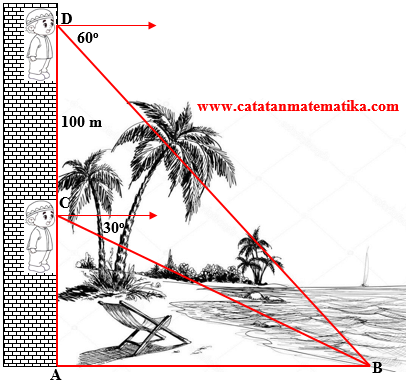
Dari puncak gedung bertingkat Johan melihat pantai dengan sudut depresi $30^\circ $. Kemudian Johan naik sejauh 100 meter dan melihat kembali pantai dengan sudut depresi $60^\circ $. Jarak gedung ke pantai adalah … meter.
A. 20
B. 25
C. 50
D. $50\sqrt{2}$
E. $50\sqrt{3}$

Penyelesaian: Lihat/Tutup

Perhatikan gambar berikut!
Soal Hots Sudut-sudut Istimewa dan Pembahasan

Soal Hots Sudut-sudut Istimewa dan Pembahasan

Perhatikan segitiga ADB:
$\begin{align} \angle D &=\angle ADB \\ &=90^\circ -60^\circ \\ \angle D &=30^\circ \end{align}$
$\begin{align}\tan D &=\frac{AB}{DA} \\ \tan 30^\circ &=\frac{AB}{DC+CA} \\ \frac{1}{\sqrt{3}} &=\frac{AB}{100+CA} \\ 100+CA &=\sqrt{3}.AB \\ CA &=\sqrt{3}.AB-100 \end{align}$
Perhatikan segitiga CAB:
$\begin{align} \angle C &=\angle ACB \\ &=90^\circ -30^\circ \\ \angle C &=60^\circ \end{align}$
$\begin{align} \tan C &=\frac{AB}{CA} \\ \tan 60^\circ &=\frac{AB}{CA} \\ \sqrt{3} &=\frac{AB}{CA} \\ \sqrt{3}.CA &=AB \\ CA &=\frac{AB}{\sqrt{3}} \\ \sqrt{3}AB-100 &=\frac{AB}{\sqrt{3}} \\ 3AB-100\sqrt{3} &=AB \\ 2AB &=100\sqrt{3} \\ AB &=50\sqrt{3} \end{align}$
Jadi, jarak gedung ke pantai adalah $50\sqrt{3}$ m.
Jawaban: E

Soal No. 17 (Soal HOTS)

Seorang anak tingginya 1,63 meter berdiri pada jarak 15 meter dari kaki tiang bendera. Ia melihat puncak tiang bendera dengan sudut $45^\circ $ dengan arah mendatar, maka tinggi tiang bendera itu adalah … meter.
A. 15
B. $15\sqrt{2}$
C. 16,63
D. 16,63$\sqrt{2}$
E. 18,63

Penyelesaian: Lihat/Tutup

Perhatikan sketsa gambar berikut!
Soal Hots Sudut-sudut Istimewa dan Pembahasan

Soal Hots Sudut-sudut Istimewa dan Pembahasan

Pada segitiga ABC:
AB = 15 m
$\begin{align} \tan A &=\frac{BC}{AB} \\ \tan 45^\circ &=\frac{BC}{15} \\ 1 &=\frac{BC}{15} \\ BC &=15 \end{align}$
Tinggi tiang bendera
= 1,63 cm + BC
= 1,63 m + 15 m
= 16,63 m
Jawaban: C

Semoga postingan: Soal Perbandingan Trigonometri Sudut Istimewa dan Pembahasan ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Post a Comment for "Soal Perbandingan Trigonometri Sudut Istimewa dan Pembahasan"

Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.