Soal Perbandingan Trigonometri pada Segitiga Siku-siku dan Pembahasan

Berikut ini adalah Soal dan Pembahasan Perbandingan Trigonometri yaitu salah satu sub materi TRIGONOMETRI bidang studi Matematika.

Soal No. 1

Pada segitiga PQR di bawah ini, $\sin \beta $ = …

A. $\frac{p}{q}$
B. $\frac{p}{r}$
C. $\frac{r}{q}$
D. $\frac{q}{p}$
E. $\frac{r}{p}$

Penyelesaian: Lihat/Tutup

$\sin \beta =\frac{\text{sisi}\,\text{depan}}{\text{sisi}\,\text{miring}}=\frac{q}{p}$
Jawaban: D

---

Soal No. 2

Pada segitiga KLM di bawah ini nilai dari $\sin \alpha +\sin \beta $ = …

A. $\frac{12}{10}$
B. $\frac{14}{10}$
C. $\frac{16}{10}$
D. $\frac{18}{10}$
E. $\frac{20}{10}$

Penyelesaian: Lihat/Tutup

$\begin{align} \sin \alpha +\sin \beta &=\frac{ML}{KL}+\frac{KM}{KL} \\ &=\frac{8}{10}+\frac{6}{10} \\ \sin \alpha +\sin \beta &=\frac{14}{10} \end{align}$
Jawaban: B

---

Soal No. 3

Jika $\sin \alpha =\frac{12}{13}$, dengan $\alpha $ lancip maka $\cos \alpha $ = ….
A. $\frac{13}{12}$
B. $\frac{13}{5}$
C. $\frac{5}{13}$
D. $\frac{12}{5}$
E. $\frac{5}{12}$

Penyelesaian: Lihat/Tutup

$\sin \alpha =\frac{12}{13}=\frac{de}{mi}$
$\begin{align} sa &=\sqrt{mi^2-de^2} \\ &=\sqrt{{{13}^2}-{{12}^2}} \\ &=\sqrt{169-144} \\ &=\sqrt{25} \\ sa &=5 \end{align}$
$\cos \alpha =\frac{sa}{mi}=\frac{5}{13}$
Jawaban: C

---

Soal No. 4

Jika $\cos A=\frac{2}{3}$, dengan A lancip maka $\tan A$ = …
A. $\frac{1}{3}\sqrt{5}$
B. $\frac{3}{2}$
C. $\frac{2}{5}\sqrt{5}$
D. $\frac{1}{2}\sqrt{5}$
E. $\frac{3}{5}\sqrt{5}$

Penyelesaian: Lihat/Tutup

$\cos A=\frac{2}{3}=\frac{sa}{mi}$
$\begin{align} de &=\sqrt{mi^2-sa^2} \\ &=\sqrt{{{3}^2}-{{2}^2}} \\ &=\sqrt{9-4} \\ de &=\sqrt{5} \end{align}$
$\tan A=\frac{de}{sa}=\frac{\sqrt{5}}{2}$
Jawaban: D

---

Soal No. 5

Jika $\tan A=3$, dengan A lancip maka $\sin A$ = ….
A. $\frac{1}{3}\sqrt{10}$
B. $\frac{8}{10}\sqrt{10}$
C. $\frac{10}{3}\sqrt{10}$
D. $\frac{3}{10}\sqrt{10}$
E. $\frac{1}{10}\sqrt{10}$

Penyelesaian: Lihat/Tutup

$\tan A=3=\frac{3}{1}=\frac{de}{sa}$
$\begin{align} mi &=\sqrt{de^2+sa^2} \\ &=\sqrt{3^2+1^2} \\ &=\sqrt{9+1} \\ mi &=\sqrt{10} \end{align}$
$\begin{align} \sin A &=\frac{de}{mi} \\ &=\frac{3}{\sqrt{10}} \\ &=\frac{3}{\sqrt{10}}\times \frac{\sqrt{10}}{\sqrt{10}} \\ \sin A &=\frac{3}{10}\sqrt{10} \end{align}$
Jawaban: D

---

Soal No. 6

Bila $0^\circ < a < 90^\circ $ dan $\tan a=\frac{5}{\sqrt{11}}$, maka $\sin a$ = …
A. $\frac{5}{6}$
B. $\frac{25}{36}$
C. $\frac{1}{6}\sqrt{11}$
D. $\frac{5}{36}$
E. $\frac{1}{36}\sqrt{11}$

Penyelesaian: Lihat/Tutup

$\tan a=\frac{5}{\sqrt{11}}=\frac{de}{sa}$
$\begin{align} mi &=\sqrt{de^2+sa^2} \\ &=\sqrt{{{5}^2}+{{(\sqrt{11})}^2}} \\ &=\sqrt{25+11} \\ &=\sqrt{36} \\ mi &=6 \end{align}$
$\sin a=\frac{de}{mi}=\frac{5}{6}$
Jawaban: A

---

Soal No. 7

Pada gambar disamping nilai $\cos \angle BAC$ adalah ….

A. $\frac{15}{40}$
B. $\frac{15}{25}$
C. $\frac{15}{20}$
D. $\frac{20}{25}$
E. $\frac{25}{40}$

Penyelesaian: Lihat/Tutup

$\begin{align} AC &=\sqrt{A{{B}^2}-B{{C}^2}} \\ & =\sqrt{{{25}^2}-{{15}^2}} \\ & =\sqrt{625-225} \\ & =\sqrt{400} \\ AC &=20 \end{align}$
$\cos \angle BAC=\frac{AC}{AB}=\frac{20}{25}$
Jawaban: D

---

Soal No. 8

Jika $\cos x=2\sin x$, nilai $\sin x\cos x$ adalah …
A. $\frac{1}{5}$
B. $\frac{1}{4}$
C. $\frac{1}{3}$
D. $\frac{2}{5}$
E. $\frac{2}{3}$

Penyelesaian: Lihat/Tutup

$\begin{align} \cos x &=2\sin x \\ \frac{1}{2} &=\frac{\sin x}{\cos x} \\ \tan x=\frac{1}{2} &=\frac{de}{sa} \end{align}$
$\begin{align} mi &=\sqrt{de^2+sa^2} \\ & =\sqrt{1^2+2^3} \\ mi &=\sqrt{5} \end{align}$
$\begin{align} \sin x\cos x &=\frac{de}{mi}\times \frac{sa}{mi} \\ &= \frac{1}{\sqrt{5}}\times \frac{2}{\sqrt{5}} \\ \sin x.\cos x &=\frac{2}{5} \end{align}$
Jawaban: D

---

Soal No. 9

Apabila $4\cot x=3$ dengan sudut $x$ lancip maka nilai dari $\frac{\sin x-\cos x}{\sin x+\cos x}$ = ….
A. $-\frac{1}{7}$
B. 0
C. $\frac{1}{7}$
D. $\frac{7}{3}$
E. $\frac{3}{7}$

Penyelesaian: Lihat/Tutup

$4\cot x=3\Leftrightarrow \cot x=\frac{3}{4}$
$\begin{align}\frac{\sin x-\cos x}{\sin x+\cos x} &=\frac{\frac{\sin x}{\sin x}-\frac{\cos x}{\sin x}}{\frac{\sin x}{\sin x}+\frac{\cos x}{\sin x}} \\ &= \frac{1-\cot x}{1+\cot x} \\ &= \frac{1-\frac{3}{4}}{1+\frac{3}{4}} \\ \frac{\sin x-\cos x}{\sin x+\cos x} &=\frac{1}{7} \end{align}$
Jawaban: C

---

Soal No. 10

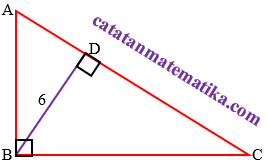
Perhatikan gambar berikut!

Diketahui $\Delta ABC$ siku-siku di B, $\cos \alpha =\frac{12}{13}$, dan $\tan \beta =1$. Jika$AD=a$, maka $AC$ = …
A. $\frac{1}{2}a$
B. $\frac{11}{7}a$
C. $\frac{12}{7}a$
D. $\frac{13}{7}a$
E. $2a$

Penyelesaian: Lihat/Tutup

Perhatikan segitiga CBD:
$\begin{align} \cos \alpha &=\frac{12}{13} \\ \frac{AB}{AC} &=\frac{12}{13} \end{align}$
$\begin{align} BC &=\sqrt{A{{C}^2}-A{{B}^2}} \\ &=\sqrt{{{13}^2}-{{12}^2}} \\ BC &=5 \end{align}$
$\begin{align} \tan \beta &=1 \\ \frac{BC}{BD} &=1 \\ BC&=BD=5 \end{align}$
$\begin{align} AB &=AD+BD \\ 12 &=a+5 \\ a &=7 \end{align}$
$\begin{align} AC &=13 \\ &=\frac{13}{7}\times 7 \\ AC &=\frac{13}{7}a \end{align}$
Jawaban: D

---

Soal No. 11

Jika $\sin x=k$, maka $\frac{1-{{\tan }^2}x}{1+{{\tan }^2}x}$ = ….
A. $1+k$
B. $1+k^2$
C. $1+2k^2$
D. $1-2k^2$
E. 1

Penyelesaian: Lihat/Tutup

$\begin{align} \sin x &=k \\ \frac{de}{mi} &=\frac{k}{1} \\ sa &=\sqrt{mi^2-de^2} \\ sa &=\sqrt{1-k^2} \end{align}$
$\tan x=\frac{de}{sa}=\frac{k}{\sqrt{1-k^2}}$
${{\tan }^2}x=\frac{k^2}{1-k^2}$
$\begin{align} \frac{1-{{\tan }^2}x}{1+{{\tan }^2}x} &=\frac{1-\frac{k^2}{1-k^2}}{1-\frac{k^2}{1-k^2}} \\ &=\frac{\frac{1-k^2-k^2}{1-k^2}}{\frac{1-k^2+k^2}{1-k^2}} \\ \frac{1-{{\tan }^2}x}{1+{{\tan }^2}x} &=1-2k^2 \end{align}$
Jawaban: D

---

Soal No. 12

Jika $\tan \alpha =-p$ dengan $\alpha $ sudut lancip maka $\sin \alpha $ = …
A. $\frac{-2p}{\sqrt{p^2+1}}$
B. $\frac{-p}{\sqrt{p^2+1}}$
C. $\frac{p}{\sqrt{p^2+1}}$
D. $\frac{2p}{\sqrt{p^2+1}}$
E. $\frac{1}{\sqrt{p^2+1}}$

Penyelesaian: Lihat/Tutup

$\begin{align} \tan \alpha &=-p \\ \frac{de}{sa} &=\frac{-p}{1} \\ mi &=\sqrt{de^2+sa^2} \\ &=\sqrt{{{(-p)}^2}+1^2} \\ mi &=\sqrt{p^2+1} \end{align}$
$\sin \alpha =\frac{de}{mi}=\frac{-p}{\sqrt{p^2+1}}$
Jawaban: B

---

Soal No. 13

Jika $0 < x < \frac{\pi }{2}$ dan $x$ memenuhi persamaan $6{{\sin }^2}x-\sin x-1=0$, maka $\cos x$ = ….
A. $\frac{2\sqrt{3}}{3}$
B. $\frac{\sqrt{3}}{2}$
C. $\frac{\sqrt{2}}{3}$
D. $\frac{\sqrt{3}}{3}$
E. $\frac{\sqrt{3}}{4}$

Penyelesaian: Lihat/Tutup

Misal:
$\sin x=p$ maka:
$\begin{align} 6{{\sin }^2}x-\sin x-1 &=0 \\ 6p^2-p-1 &=0 \\ (3p+1)(2p-1) &=0 \end{align}$
$\begin{align} p &=-\frac{1}{3} \\ \sin x &=-\frac{1}{3} \end{align}$ atau $\begin{align} p &=\frac{1}{2} \\ \sin x &=\frac{1}{2} \end{align}$
Karena $0 < x < \frac{\pi }{2}$ maka yang memenuhi adalah:
$\begin{align} \sin x &=\frac{1}{2} \\ \frac{de}{mi} &=\frac{1}{2} \\ sa &=\sqrt{mi^2-de^2} \\ &=\sqrt{{{2}^2}-1^2} \\ sa &=\sqrt{3} \\ \cos x &=\frac{sa}{mi}=\frac{\sqrt{3}}{2} \end{align}$
Jawaban: B

---

Soal No. 14

Apabila $\tan \theta =\frac{1}{\sqrt{7}}$ maka nilai dari $\frac{{{\csc }^2}\theta -{{\sec }^2}\theta }{{{\csc }^2}\theta +{{\sec }^2}\theta }$ adalah ….
A. $\frac{1}{12}$
B. $\frac{3}{7}$
C. $\frac{3}{4}$
D. $\frac{5}{7}$
E. $\frac{4}{3}$

Penyelesaian: Lihat/Tutup

$\begin{align} \frac{{{\csc }^2}\theta -{{\sec }^2}\theta }{{{\csc }^2}\theta +{{\sec }^2}\theta } &=\frac{\frac{1}{{{\sin }^2}\theta }-\frac{1}{{{\cos }^2}\theta }}{\frac{1}{{{\sin }^2}\theta }+\frac{1}{{{\cos }^2}\theta }} \\ &=\frac{1-{{\tan }^2}\theta }{1+{{\tan }^2}\theta } \\ &=\frac{1-{{\left( \frac{1}{\sqrt{7}} \right)}^2}}{1+{{\left( \frac{1}{\sqrt{7}} \right)}^2}} \\ &=\frac{1-\frac{1}{7}}{1+\frac{1}{7}} \\ &=\frac{6}{8} \\ \frac{{{\csc }^2}\theta -{{\sec }^2}\theta }{{{\csc }^2}\theta +{{\sec }^2}\theta } &=\frac{3}{4} \end{align}$
Jawaban: C

---

Soal No. 15

Apabila $\tan A=t$ dengan A sudut lancip, maka $\sin A$ = ….
A. $1+{{t}^2}$
B. $1-{{t}^2}$
C. $\sqrt{\frac{1}{{{t}^2}+1}}$
D. $\sqrt{{{t}^2}+1}$
E. $\sqrt{\frac{{{t}^2}}{{{t}^2}+1}}$

Penyelesaian: Lihat/Tutup

$\begin{align} \tan A &=t \\ \frac{de}{sa} &=\frac{t}{1} \\ mi &=\sqrt{de^2+sa^2}=\sqrt{{{t}^2}+1} \\ \sin A &=\frac{de}{mi} \\ &=\frac{t}{\sqrt{{{t}^2}+1}} \\ \sin A &=\sqrt{\frac{{{t}^2}}{{{t}^2}+1}} \end{align}$
Jawaban: E

---

Soal No. 16

Pada segitiga ABC siku-siku di B dengan $\cos C=\frac{1}{3}$. Jika BD adalah garis tinggi pada sisi AC dan BD = 6 cm, maka panjang AC = … cm.
A. $4\sqrt{2}$
B. $\frac{27}{2}\sqrt{2}$
C. $5\sqrt{2}$
D. $\frac{11}{2}\sqrt{2}$
E. $6\sqrt{2}$

Penyelesaian: Lihat/Tutup

 
Perhatikan segitiga BDC:
$\begin{align} \cos C &=\frac{CD}{BC} \\ \frac{1}{3} &=\frac{CD}{BC} \\ BC &=3CD \end{align}$
Teorema pythagoras:
$\begin{align} B{{C}^2} &=B{{D}^2}+C{{D}^2} \\ {{(3CD)}^2} &={{6}^2}+C{{D}^2} \\ 9C{{D}^2} &=36+C{{D}^2} \\ 8C{{D}^2} &=36 \\ C{{D}^2} &=\frac{36}{8}=\frac{9}{2} \\ CD &=\frac{3}{\sqrt{2}} \end{align}$
$\begin{align} BC &=3CD \\ &=3.\frac{3}{\sqrt{2}} \\ BC &=\frac{9}{\sqrt{2}} \end{align}$
Perhatikan segitiga ABC:
$\begin{align} \cos C &=\frac{BC}{AC} \\ \frac{1}{3} &=\frac{\frac{9}{\sqrt{2}}}{AC} \\ AC &=\frac{27}{\sqrt{2}}=\frac{27}{2}\sqrt{2} \end{align}$
Jawaban: B

---

Soal No. 17

Perhatikan gambar berikut!

Nilai $\sin \theta $ dari segitiga di atas adalah …
A. $\frac{b}{c}$
B. $\frac{a}{c}$
C. $\frac{b}{a}$
D. $\frac{c}{d}$
E. $\frac{c}{a}$

Penyelesaian: Lihat/Tutup

$\sin \alpha =\frac{\text{sisi}\,\text{depan}}{\text{hipotenusa}}=\frac{a}{c}$
Jawaban: B

---

Soal No. 18

Diketahui sin A = $\frac{p}{q}$ dengan $0^\circ < A < 90^\circ $ maka nilai dari ${{\cos }^2}A$ = ….
A. $\frac{p^2}{p^2+q^2}$
B. $\frac{p^2}{p^2-q^2}$
C. $\frac{q^2}{p^2-q^2}$
D. $\frac{q^2+p^2}{q^2}$
E. $\frac{q^2-p^2}{q^2}$

Penyelesaian: Lihat/Tutup

$\sin A=\frac{p}{q}=\frac{de}{mi}$
$sa=\sqrt{mi^2-de^2}=\sqrt{q^2-p^2}$
$\begin{align} {{\cos }^2}A &={{\left( \frac{sa}{mi} \right)}^2} \\ &={{\left( \frac{\sqrt{q^2-p^2}}{q} \right)}^2} \\ {{\cos }^2}A &=\frac{q^2-p^2}{q^2} \end{align}$
Jawaban: E

---

Soal No. 19

Diketahui nilai $\tan \alpha =\frac{1}{3}$ untuk $0^\circ < \alpha < 90^\circ $. Nilai dari $2\sin \alpha .\cos \alpha $ = …
A. $\frac{3}{5}$
B. $\frac{2}{5}$
C. $\frac{1}{5}$
D. $-\frac{2}{5}$
E. $-\frac{3}{5}$

Penyelesaian: Lihat/Tutup

$\tan \alpha =\frac{1}{3}=\frac{de}{sa}$
$\begin{align} mi &=\sqrt{de^2+sa^2} \\ &=\sqrt{1^2+3^2} \\ mi &=\sqrt{10} \end{align}$
$\begin{align} 2\sin \alpha .\cos \alpha &=2.\frac{de}{mi}.\frac{sa}{mi} \\ &=2.\frac{1}{\sqrt{10}}.\frac{3}{\sqrt{10}} \\ &=\frac{6}{10} \\ 2\sin \alpha .\cos \alpha &=\frac{3}{5} \end{align}$
Jawaban: A

---

Soal No. 20

Diketahui nilai dari $\sin 25^\circ =p$. Nilai dari $\tan 25^\circ $ = …
A. $\sqrt{1-p^2}$
B. $\sqrt{1+p^2}$
C. $\frac{p}{\sqrt{1-p^2}}$
D. $\frac{p}{\sqrt{1+p^2}}$
E. $\frac{2p}{\sqrt{1+p^2}}$

Penyelesaian: Lihat/Tutup

$\sin 25^\circ =p\Leftrightarrow \frac{de}{mi}=\frac{p}{1}$
$sa=\sqrt{mi^2-de^2}=\sqrt{1-p^2}$
$\tan 25^\circ =\frac{de}{sa}=\frac{p}{\sqrt{1-p^2}}$
Jawaban: C

---

Semoga postingan: Soal Perbandingan Trigonometri pada Segitiga Siku-siku dan Pembahasan ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :