Pembahasan SBMPTN 2014 Matematika IPA Kode 591
Mari kita bahas tuntas Matematika IPA SBMPTN 2014 Kode 591. Fokus, tuntas, dan lulus perguruan tinggi negeri, mari wujudkan kebanggaan orang tua terhadap diri mu.
Matematika IPA SBMPTN 2014 No. 1
Diketahui $a$, $a+b$, dan $4a+b$ merupakan 3 suku berurutan suatu barisan aritmetika. Jika $a$, $a+b$, $4a+b+9$ merupakan suatu barisan geometri, maka $a+b$ = …
A. 2
B. 3
C. 4
D. 5
E. 6
Pembahasan:
BA: $a$, $a+b$, $4a+b$
$2{{U}_{2}}={{U}_{1}}+{{U}_{3}}$
$2(a+b)=a+4a+b$
$2a+2b=5a+b$
$b=3a$
BG: $a$, $a+b$, $4a+b+9$
$U_{2}^{2}={{U}_{1}}.{{U}_{3}}$
${{(a+b)}^{2}}=a(4a+b+9)$, ingat: $b=3a$, maka:
${{(a+3a)}^{2}}=a(4a+3a+9)$
$16{{a}^{2}}=7{{a}^{2}}+9a$
$9{{a}^{2}}-9a=0$
$9a(a-1)=0$
$a=1\Leftrightarrow b=3a=3$
$a+b=1+3=4$
Jawaban: C
Matematika IPA SBMPTN 2014 No. 2
Jika $\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{Ax+B}-2}{x}=1$, maka …
A. $B={{A}^{2}}$
B. $4{{B}^{2}}=A$
C. $4B={{A}^{2}}$
D. $4B=A$
E. $A+B=0$
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{Ax+B}-2}{x}=1$, dengan teorema L’HOSPITAL, maka:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{\frac{A}{2\sqrt{Ax+B}}}{1}=1$
$\frac{A}{2\sqrt{A.0+B}}=1$
$A=2\sqrt{B}\Leftrightarrow 4B={{A}^{2}}$
Jawaban: C
Matematika IPA SBMPTN 2014 No. 3
Semua nilai $x$ yang memenuhi pertidaksamaan $^{|1-x|}\log (x+5) > 2$ adalah …
A. $-1 < x < 1$
B. $-1 < x < 0$ atau $2 < x < 4$
C. $-5 < x < 1$
D. $-1 < x < 0$ atau $1 < x < 4$
E. $1 < x < 2$
Pembahasan:
*) syarat numerus:
$x+5 > 0 \Leftrightarrow x > -5$
**) syarat bilangan pokok:
$|x-1| > 0$ maka $x < 1$ atau $x > 1$
$|x-1| \ne 1$ maka $x \ne 2$ dan $x \ne 0$
***)
$^{|1-x|}\log (x+5) > 2$
$x+5 > |x-1{{|}^{2}}$
$x+5 > {{x}^{2}}-2x+1$
${{x}^{2}}-3x-4 < 0$
$(x+1)(x-4) < 0$
$-1 < x < 4$
Dari *), **), dan ***) diperoleh:
Himpunan penyelesaiannya adalah:
$-1 < x < 0$, $0 < x < 1$, $1 < x < 2$, $2 < x < 4$
Dan yang memenuhi adalah opsi B.
Jawaban: B
Matematika IPA SBMPTN 2014 No. 4
Diketahui P dan Q suatu polinomial sehingga $P(x).Q(x)$ dibagi ${{x}^{2}}-1$ bersisa $3x+5$. Jika $Q(x)$ dibagi $x-1$ bersisa 4, maka $P(x)$ dibagi $x-1$ bersisa …
A. 8
B. 6
C. 4
D. 2
E. 1
Pembahasan:
Teorema Sisa: Jika $f(x):(x-k)$ maka sisa = $f(k)$.
$Q(x):(x-1)$ maka sisa = $Q(1)=4$
Dengan persamaan pembagian suku banyak:
Yang dibagi = Pembagi x hasil + sisa
$P(x).Q(x)=({{x}^{2}}-1).hasil+3x+5$
$P(x).Q(x)=(x+1)(x-1).hasil+3x+5$
Substitusi nilai $x=1$, maka:
$P(1).Q(1)=(1+1)(1-1).hasil+3.1+5$
$P(1).Q(1)=8$
$P(1).4=8\Leftrightarrow P(1)=2$
$P(x):(x-1)$ maka sisa = $P(1)=2$
Jawaban: D
Matematika IPA SBMPTN 2014 No. 5
Banyaknya akar real $f(t)={{t}^{9}}-t$ adalah … buah.
A. 2
B. 3
C. 4
D. 6
E. 9
Pembahasan:
$f(t)={{t}^{9}}-t=0$
$t({{t}^{8}}-1)=0$
$t({{t}^{4}}+1)({{t}^{4}}-1)=0$
$t({{t}^{4}}+1)({{t}^{2}}+1)({{t}^{2}}-1)=0$
$t({{t}^{4}}+1)({{t}^{2}}+1)(t+1)(t-1)=0$
${{t}_{1}}=0,{{t}_{2}}=-1,{{t}_{3}}=1$
Jadi, hanya ada 3 nilai t yang real.
Jawaban: B
Matematika IPA SBMPTN 2014 No. 6
Misalkan ${{l}_{1}}$ dan ${{l}_{2}}$ menyatakan garis yang menyinggung lingkaran ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ berturut-turut di ${{P}_{1}}({{x}_{1}},{{y}_{1}})$ dan ${{P}_{2}}({{x}_{2}},{{y}_{2}})$. Jika ${{l}_{1}}$ dan ${{l}_{2}}$ berpotongan di $(2,-1)$ dan titik $(4,-1)$ berada pada garis yang melalui ${{P}_{1}}$ dan ${{P}_{2}}$, maka $r$ = …
A. 6
B. 5
C. 4
D. 3
E. 2
Pembahasan:
*) secara hitungan menggunakan rumus garis polar diperoleh r = 3.
*) Tetapi tidak memenuhi syarat, karena jarak titik pusat (0,0) terhadap titik potong (2,-1) < r.
Kesimpulan: soal keliru
Jawaban: -
Matematika IPA SBMPTN 2014 No. 7
Bila $\sin ({{40}^{o}}+x)=a$, ${{0}^{o}}
A. $\frac{\sqrt{1-{{a}^{2}}}-a}{2}$
B. $\frac{\sqrt{3(1-{{a}^{2}})}-a}{2}$
C. $\frac{\sqrt{3(1-{{a}^{2}})}+a}{2}$
D. $\frac{\sqrt{2(1-{{a}^{2}})}+a}{2}$
E. $\frac{\sqrt{2(1-{{a}^{2}})}-a}{2}$
Pembahasan:
$\sin ({{40}^{o}}+x)=a$
$\frac{de}{mi}=\frac{a}{1}\Rightarrow sa=\sqrt{1-{{a}^{2}}}$
$\cos ({{40}^{o}}+x)=\frac{sa}{mi}=\frac{\sqrt{1-{{a}^{2}}}}{1}=\sqrt{1-{{a}^{2}}}$
$\cos ({{70}^{o}}+x)=\cos [(40+x)+30]$
$=\cos (40+x).\cos 30-\sin (40+x).\sin 30$
$=\sqrt{1-{{a}^{2}}}.\frac{1}{2}\sqrt{3}-a.\frac{1}{2}$
$=\frac{\sqrt{3(1-{{a}^{2}})}-a}{2}$
Jawaban: B
Matematika IPA SBMPTN 2014 No. 8
Jika $A\left[ \begin{matrix} 1 \\ 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right]$ dan $A\left[ \begin{matrix} -1 \\ 2 \\ \end{matrix} \right]=\left[ \begin{matrix} -5 \\ -6 \\ \end{matrix} \right]$, maka $A\left[ \begin{matrix} 2 & -5 \\ 0 & 6 \\ \end{matrix} \right]$ = …
A. $\left[ \begin{matrix} 4 & 14 \\ 8 & 12 \\ \end{matrix} \right]$
B. $\left[ \begin{matrix} 2 & -16 \\ 4 & -18 \\ \end{matrix} \right]$
C. $\left[ \begin{matrix} 2 & 14 \\ 4 & 12 \\ \end{matrix} \right]$
D. $\left[ \begin{matrix} 4 & -8 \\ 8 & 8 \\ \end{matrix} \right]$
E. $\left[ \begin{matrix} 4 & -19 \\ 8 & -26 \\ \end{matrix} \right]$
Pembahasan:
$A\left[ \begin{matrix} 1 \\ 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 2 \\ 4 \\ \end{matrix} \right]$ dan $A\left[ \begin{matrix} -1 \\ 2 \\ \end{matrix} \right]=\left[ \begin{matrix} -5 \\ -6 \\ \end{matrix} \right]$, maka:
$A\left[ \begin{matrix} 1 & -1 \\ 0 & 2 \\ \end{matrix} \right]=\left[ \begin{matrix} 2 & -5 \\ 4 & -6 \\ \end{matrix} \right]$
$A=\left[ \begin{matrix} 2 & -5 \\ 4 & -6 \\ \end{matrix} \right].{{\left[ \begin{matrix} 1 & -1 \\ 0 & 2 \\ \end{matrix} \right]}^{-1}}$
$A=\left[ \begin{matrix} 2 & -5 \\ 4 & -6 \\ \end{matrix} \right].\frac{1}{2-0}\left[ \begin{matrix} 2 & -1 \\ 0 & 1 \\ \end{matrix} \right]$
$A=\frac{1}{2}\left[ \begin{matrix} 4 & -3 \\ 8 & -2 \\ \end{matrix} \right]$
$A=\left[ \begin{matrix} 2 & \frac{-3}{2} \\ 4 & -1 \\ \end{matrix} \right]$
$A\left[ \begin{matrix} 2 & -5 \\ 0 & 6 \\ \end{matrix} \right]=\left[ \begin{matrix} 2 & \frac{-3}{2} \\ 4 & -1 \\ \end{matrix} \right]\left[ \begin{matrix} 2 & -5 \\ 0 & 6 \\ \end{matrix} \right]$
$A\left[ \begin{matrix} 2 & -5 \\ 0 & 6 \\ \end{matrix} \right]=\left[ \begin{matrix} 4 & -19 \\ 8 & -26 \\ \end{matrix} \right]$
Jawaban: E
Matematika IPA SBMPTN 2014 No. 9
Jika $p$ dan $q$ merupakan akar-akar persamaan kuadrat: ${{x}^{2}}-(a+1)x+\left( -a-\frac{5}{2} \right)=0$ maka nilai minimum ${{p}^{2}}+{{q}^{2}}$ adalah …
A. $\frac{5}{2}$
B. 2
C. 1
D. $\frac{1}{2}$
E. 0
Pembahasan:
${{x}^{2}}-(a+1)x+\left( -a-\frac{5}{2} \right)=0$ akar-akarnya $p$ dan $q$, maka:
${{p}^{2}}+{{q}^{2}}={{(p+q)}^{2}}-2pq$
${{p}^{2}}+{{q}^{2}}={{(-a-1)}^{2}}-2\left( -a-\frac{5}{2} \right)$
${{p}^{2}}+{{q}^{2}}={{a}^{2}}+2a+1+2a+5$
${{p}^{2}}+{{q}^{2}}={{a}^{2}}+4a+6$
Nilai minimum diperoleh jika:
$\frac{d}{da}\left( {{p}^{2}}+{{q}^{2}} \right)=0$
$2a+4=0\Leftrightarrow a=-2$
Substitusi ke:
${{p}^{2}}+{{q}^{2}}={{a}^{2}}+4a+6$
${{p}^{2}}+{{q}^{2}}={{(-2)}^{2}}+4(-2)+6=2$
Jawaban: B
Matematika IPA SBMPTN 2014 No. 10
Diketahui suatu parabola simetris terhadap garis $x=-2$, dan garis singgung parabola di titik $(0,1)$ sejajar garis $4x+y=4$. Titik puncak parabola adalah …
A. (-2,-3)
B. (-2,-2)
C. (-2,0)
D. (-2,1)
E. (-2,5)
Pembahasan:
Misalkan parabola $y=a{{x}^{2}}+bx+c$
Sumbu simetris $x=-2$ maka:
${{x}_{p}}=\frac{-b}{2a}=-2\Leftrightarrow b=4a$
Garis singgung melalui titik (0,1)
$y=a{{x}^{2}}+bx+c\Leftrightarrow 1=c$
Garis singgung sejajar $4x+y=4$ maka:
$m=-4$
$y'=4$ untuk $x=0$
$2a.0+b=-4\Leftrightarrow b=-4$
$b=4a\Leftrightarrow -4=4a\Leftrightarrow a=-1$
Sehingga:
$y=a{{x}^{2}}+bx+c$
$y=-{{x}^{2}}-4x+1$ dan ${{x}_{p}}=-2$
${{y}_{p}}=-{{(-2)}^{2}}-4(-2)+1=5$
Puncak parabola $(-2,5)$
Jawaban: E
Matematika IPA SBMPTN 2014 No. 11
Jika $s=1+\frac{1}{2}\sin 2x+\frac{1}{4}{{\sin }^{2}}2x+\frac{1}{8}{{\sin }^{3}}2x+...$ , maka …
A. $\frac{2}{3}< s < 2$
B. $\frac{3}{2} < s < 2$
C. $\frac{2}{3} < s < \frac{3}{2}$
D. $\frac{1}{2} < s < \frac{3}{2}$
E. $\frac{1}{2} < s < \frac{2}{3}$
Pembahasan:
Barisan Geometri Tak Hingga:
$a=1$ dan $r=\frac{1}{2}\sin 2x$
$s=\frac{a}{1-r}$
$s=\frac{1}{1-\frac{1}{2}\sin 2x}$
$s=\frac{2}{2-\sin 2x}$
Jika $\sin 2x=1$ maka $s=\frac{2}{2-1}=2$
Jika $\sin 2x=-1$ maka $s=\frac{2}{2-(-1)}=\frac{2}{3}$
Kesimpulan: $\frac{2}{3} < s < 2$
Jawaban: A
Matematika IPA SBMPTN 2014 No. 12
Banyak cara menempatkan 10 kelereng identik ke dalam 5 kotak dengan setiap memuat paling sedikit 1 kelereng adalah …
A. 63
B. 120
C. 126
D. 252
E. 3024
Pembahasan:
Misalkan kelima kotak itu adalah:
A, B, C, D, E
Maka kemungkinan-kemungkinan isi kelima kotak tersebut adalah:
6, 1, 1, 1, 1 = $\frac{5!}{4!}=5$
5, 2, 1, 1, 1 = $\frac{5!}{3!}=20$
4, 3, 1, 1, 1 = $\frac{5!}{3!}=20$
4, 2, 2, 1, 1 = $\frac{5!}{2!.2!}=30$
3, 3, 2, 1, 1 = $\frac{5!}{2!.2!}=30$
3, 2, 2, 2, 1 = $\frac{5!}{3!}=20$
2, 2, 2, 2, 2 = 1
Seluruhnya = 126
Jawaban: C
Matematika IPA SBMPTN 2014 No. 13
Vektor-vektor $\vec{u}$, $\vec{v}$, dan $\vec{x}$ tidak nol. Vektor $\vec{u}+\vec{v}$ tegak lurus $\vec{u}-\vec{x}$, jika …
A. $|\vec{u}+\vec{v}|=|\vec{u}-\vec{v}|$
B. $|\vec{v}|=|\vec{x}|$
C. $\vec{u}.\vec{u}=\vec{v}.\vec{v},\vec{v}=-\vec{x}$
D. $\vec{u}.\vec{u}=\vec{v}.\vec{v},\vec{v}=\vec{x}$
E. $\vec{u}.\vec{v}=\vec{v}.\vec{v}$
Pembahasan:
$\vec{u}+\vec{v}$ tegak lurus $\vec{u}-\vec{x}$ maka:
$(\vec{u}+\vec{v}).(\vec{u}-\vec{x})=0$
$\vec{u}.\vec{u}-\vec{u}.\vec{x}+\vec{v}.\vec{u}-\vec{v}.\vec{x}=0$, jika $\vec{v}=\vec{x}$, maka:
$\vec{u}.\vec{u}-\vec{u}.\vec{v}+\vec{v}.\vec{u}-\vec{v}.\vec{v}=0$
$\vec{u}.\vec{u}-\vec{v}.\vec{v}=0$
$\vec{u}.\vec{u}=\vec{v}.\vec{v}$, $\vec{v}=\vec{x}$
Jawaban: D
Matematika IPA SBMPTN 2014 No. 14
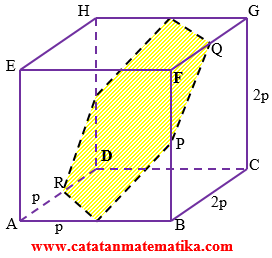
Diberikan kubus ABCD.EFGH dengan panjang rusuk $2p$. Titik-titik P, Q, R masing-masing titik tengah FB, FG, dan AD. Luas penampang irisan yang melalui P, Q, dan R dan kubus ABCD.EFGH adalah …
A. $6{{p}^{2}}\sqrt{3}$
B. $3{{p}^{2}}\sqrt{3}$
C. ${{p}^{2}}\sqrt{3}$
D. $3{{p}^{2}}\sqrt{2}$
E. $\frac{3{{p}^{2}}}{\sqrt{6}}$
Pembahasan:
Perhatikan gambar berikut ini!
Penampang irisan yang melalui P, Q, dan R membentuk bidang datar segienam beraturan dengan panjang sisi $p\sqrt{2}$.
Luas segi enam beraturan adalah:
$=6.\frac{1}{2}.p\sqrt{2}.p\sqrt{2}.\sin {{60}^{o}}$
$=3.2{{p}^{2}}.\frac{1}{2}\sqrt{3}$
$=3{{p}^{2}}\sqrt{3}$
Jawaban: B
Matematika IPA SBMPTN 2014 No. 15
Misalkan A(t) menyatakan luas daerah di bawah kurva $y=b{{x}^{2}}$, $0\le x\le t$. Jika titik $P({{x}_{0}},{{y}_{0}})$ sehingga: $A({{x}_{0}}):A(1)=1:8$, maka perbandingan luas trapesium ABPQ : DCPQ = …
A. 2 : 1
B. 3 : 1
C. 6 : 1
D. 8 : 1
E. 9 : 1
Pembahasan:
$A({{x}_{0}})=\int\limits_{0}^{{{x}_{0}}}{b{{x}^{2}}dx}$
$A({{x}_{0}})=\left. \frac{1}{3}b{{x}^{3}} \right|_{0}^{{{x}_{0}}}=\frac{1}{3}bx_{0}^{3}$
$A(1)=\int\limits_{0}^{1}{b{{x}^{2}}dx}$
$A(1)=\left. \frac{1}{3}b{{x}^{3}} \right|_{0}^{1}=\frac{1}{3}b$
$\frac{A({{x}_{0}})}{A(1)}=\frac{1}{8}$
$\frac{\frac{1}{3}bx_{0}^{3}}{\frac{1}{3}b}=\frac{1}{8}$
$x_{0}^{3}={{\left( \frac{1}{2} \right)}^{3}}\Leftrightarrow {{x}_{0}}=\frac{1}{2}$
$\frac{[ABPQ]}{[DCPQ]}=\frac{\frac{1}{2}\left( AB+PQ \right).BP}{\frac{1}{2}\left( PQ+CD \right).PC}$
$\frac{[ABPQ]}{[DCPQ]}=\frac{\frac{1}{2}\left( b+\frac{1}{4}b \right).\frac{3}{2}}{\frac{1}{2}\left( \frac{1}{4}b+b \right).\frac{1}{2}}=\frac{3}{1}$
Jawaban: B
Artikel Terkait:
|
Semoga postingan: Pembahasan SBMPTN 2014 Matematika IPA Kode 591 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Pembahasan SBMPTN 2014 Matematika IPA Kode 591"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.