Pembahasan Matematika IPA SBMPTN Tahun 2013 Kode 135
To the point aja ya...! Berikut ini adalah Pembahasan Matematika IPA SBMPTN 2013 Kode 135. yang mau download soalnya aja, silahkan...! Yang mau share soalnya juga silahkan..! mau jalan-jalan dan lihat2 pemandangan di blog Catatan Matematika juga silahkan...! Beri waktu dan tingkatkan semangat kalian ya, semoga harapan dan impian kalian untuk bisa lulus dan melanjutkan pendidikan dengan kuliah di perguruan tinggi favorit dapat tercapai. Ingat, sesungguhnya hal itu bukan hanya harapan kalian, tapi juga harapan orang tua adik-adik sekalian. Untuk itu mari bahagiakan orang tua kalian, buat mereka bangga terhadapmu. Kalian siap? Yuk pelajari dan pahami soal dan pembahasan berikut ini.
Matematika IPA SBMPTN 2013 No. 1
Persamaan lingkaran dengan pusat $(-1,1)$ dan menyinggung garis $3x-4y+12=0$ adalah …
A. ${{x}^{2}}+{{y}^{2}}+2x-2y+1=0$
B. ${{x}^{2}}+{{y}^{2}}+2x-2y-7=0$
C. $4{{x}^{2}}+4{{y}^{2}}+8x-8y-17=0$
D. ${{x}^{2}}+{{y}^{2}}+2x-2y-2=0$
E. $4{{x}^{2}}+4{{y}^{2}}+8x-8y-1=0$
Pembahasan:
Panjang jari-jari (r) adalah jarak titik $(-1,1)$ ke garis $3x-4y+12=0$, maka:
$r=\left| \frac{3{{x}_{1}}-4{{y}_{1}}+12}{\sqrt{{{3}^{2}}+{{4}^{2}}}} \right|$
$r=\left| \frac{3(-1)-4.1+12}{\sqrt{9+16}} \right|$
$r=1$
Persamaan lingkaran dengan pusat $(-1,1)$ dan r = 1 adalah:
${{(x+1)}^{2}}+{{(y-1)}^{2}}={{1}^{2}}$
${{x}^{2}}+2x+1+{{y}^{2}}-2y+1=1$
${{x}^{2}}+{{y}^{2}}+2x-2y+1=0$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 2
$\cot {{105}^{o}}\tan {{15}^{o}}$ = …
A. $-7+4\sqrt{3}$
B. $7+4\sqrt{3}$
C. $7-4\sqrt{3}$
D. $-7-4\sqrt{3}$
E. $-7+2\sqrt{3}$
Pembahasan:
$\cot {{105}^{o}}\tan {{15}^{o}}$
$=\cot ({{90}^{o}}+{{15}^{o}})\tan {{15}^{o}}$
$=-\tan {{15}^{o}}\tan {{15}^{o}}$
$=-{{\tan }^{2}}{{15}^{o}}$
$=-{{\tan }^{2}}({{60}^{o}}-{{45}^{o}})$
$=-{{\left( \frac{\tan {{60}^{o}}-\tan {{45}^{o}}}{1+\tan {{60}^{o}}.\tan {{45}^{o}}} \right)}^{2}}$
$=-{{\left( \frac{\sqrt{3}-1}{1+\sqrt{3}.1} \right)}^{2}}$
$=-\frac{3-2\sqrt{3}+1}{1+2\sqrt{3}+3}$
$=-\frac{4-2\sqrt{3}}{4+2\sqrt{3}}\times \frac{4-2\sqrt{3}}{4-2\sqrt{3}}$
$=-\frac{16-16\sqrt{3}+12}{16-12}$
$=-\frac{28-16\sqrt{3}}{4}$
$=-(7-4\sqrt{3})$
$=-7+4\sqrt{3}$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 3
Enam anak, 3 laki-laki dan 3 perempuan, duduk berjajar. Peluang 3 perempuan duduk berdampingan adalah …
A. $\frac{1}{60}$
B. $\frac{1}{30}$
C. $\frac{1}{15}$
D. $\frac{1}{10}$
E. $\frac{1}{5}$
Pembahasan:
Posisi duduk: LLLPPP maka $n(S)=P_{6}^{6}=6!$
A = kejadian 3 perempuan duduk berdampingan
Pertama: posisi duduk 3 perempuan = $P_{3}^{3}=3!$
Kedua: karena 3 perempuan selalu duduk berdampingan, maka kita anggap 1 tempat duduk digabung dengan 3 laki-laki, maka menjadi menyusun 4 tempat duduk yaitu: $P_{4}^{4}=4!$, maka:
$n(A)=3!.4!$
$P(A)=\frac{n(A)}{n(S)}=\frac{4!.3!}{6!}=\frac{4!.3.2.1}{6.5.4!}=\frac{1}{5}$
Jawaban: E
Matematika IPA SBMPTN 2013 No. 4
Jika dalam segitiga ABC diketahui $5\sin A+12\cos B=13$ dan $5\cos A+12\sin B=6\sqrt{2}$, maka $\sin C$ = …
A. $\frac{1}{2}$
B. $\frac{1}{2}\sqrt{2}$
C. $\frac{1}{2}\sqrt{3}$
D. $\sqrt{3}$
E. $\frac{3}{5}$
Pembahasan:
$5\sin A+12\cos B=13$, kuadratkan:
${{\left( 5\sin A+12\cos B \right)}^{2}}={{13}^{2}}$
$25{{\sin }^{2}}A+120\sin A\cos B+144{{\cos }^{2}}B=169$ … (1)
$5\cos A+12\sin B=6\sqrt{2}$, kuadratkan:
${{\left( 5\cos A+12\sin B \right)}^{2}}={{\left( 6\sqrt{2} \right)}^{2}}$
$25{{\cos }^{2}}A+120\cos A\sin B+144{{\sin }^{2}}B=72$ … (2)
Jumlahkan persamaan (1) dan (2), diperoleh:
$25{{\sin }^{2}}A$ + $25{{\cos }^{2}}A$ + $120\sin A\cos B$ +$120\cos A\sin B$ + $144{{\sin }^{2}}B$ + $144{{\cos }^{2}}B=169+72$
$25+120(\sin A\cos B$ + $\cos A\sin B)+144=241$
$120(\sin A\cos B$ + $\cos A\sin B)+169=241$
$120\sin (A+B)=72$
$\sin (A+B)=\frac{72}{120}=\frac{3}{5}$
Pada segitiga ABC:
${{180}^{o}}-C=A+B$
$\sin ({{180}^{o}}-C)=\sin (A+B)$
$\sin C=\frac{3}{5}$
Jawaban: E
Matematika IPA SBMPTN 2013 No. 5
Diketahui $(4,0,0)$, $B(0,-4,0)$, dan $C(0,0,8)$. Panjang vektor proyeksi $\overrightarrow{AC}$ ke vektor $\overrightarrow{AB}$ adalah ….
A. $2\sqrt{2}$
B. $\frac{3\sqrt{2}}{2}$
C. $\frac{\sqrt{2}}{3}$
D. $\sqrt{2}$
E. $\frac{\sqrt{3}}{2}$
Pembahasan:
$\overrightarrow{AC}=C-A$
$\overrightarrow{AC}=(0,0,8)-(4,0,0)=(-4,0,8)$
$\overrightarrow{AB}=B-A$
$\overrightarrow{AB}=(0,-4,0)-(4,0,0)=(-4,-4,0)$
Panjang vektor proyeksi $\overrightarrow{AC}$ ke vektor $\overrightarrow{AB}$:
$=\left| \frac{\overrightarrow{AC}.\overrightarrow{AB}}{|\overrightarrow{AB}|} \right|$
$=\left| \frac{(-4,0,8).(-4,-4,0)}{\sqrt{{{(-4)}^{2}}+{{(-4)}^{2}}+{{0}^{2}}}} \right|$
$=\left| \frac{16+0+0}{\sqrt{32}} \right|$
$=\frac{16}{4\sqrt{2}}$
$=2\sqrt{2}$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 6
Titik $(2a,-a)$ diputar ${{90}^{o}}$ berlawanan arah jarum jam dengan pusat perputaran titik $(2,2)$. Jika hasil rotasinya adalah $(a+4,-2)$ maka $a$ = …
A. 2
B. 1
C. 0
D. -1
E. -2
Pembahasan:
$R\left( (a,b),\theta \right)=R\left( (2,2),{{90}^{o}} \right)$
$\left( \begin{matrix} x' \\ y' \\ \end{matrix} \right)=\left( \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix} \right)\left( \begin{matrix} x-a \\ y-b \\ \end{matrix} \right)+\left( \begin{matrix} a \\ b \\ \end{matrix} \right)$
$\left( \begin{matrix} a+4 \\ -2 \\ \end{matrix} \right)=\left( \begin{matrix} \cos {{90}^{o}} & -\sin {{90}^{o}} \\ \sin {{90}^{o}} & \cos {{90}^{o}} \\ \end{matrix} \right)\left( \begin{matrix} 2a-2 \\ -a-2 \\ \end{matrix} \right)+\left( \begin{matrix} 2 \\ 2 \\ \end{matrix} \right)$
$\left( \begin{matrix} a+4 \\ -2 \\ \end{matrix} \right)-\left( \begin{matrix} 2 \\ 2 \\ \end{matrix} \right)=\left( \begin{matrix} 0 & -1 \\ 1 & 0 \\ \end{matrix} \right)\left( \begin{matrix} 2a-2 \\ -a-2 \\ \end{matrix} \right)$
$\left( \begin{matrix} a+2 \\ -4 \\ \end{matrix} \right)=\left( \begin{matrix} a+2 \\ 2a-2 \\ \end{matrix} \right)$
$2a-2=-4\Leftrightarrow a=-1$
Jawaban: D
Matematika IPA SBMPTN 2013 No. 7
Diketahui kubus ABCD.EFGH mempunyai sisi 4 cm. Titik P, adalah titik tengah CD, titik Q adalah titik tengah EH, dan titik R titik tengah BF. Jarak P ke QR adalah ….
A. $\sqrt{15}$
B. $3\sqrt{2}$
C. $\sqrt{6}$
D. $\sqrt{5}$
E. $2\sqrt{2}$
Pembahasan:
Perhatikan gambar berikut ini!

Perhatikan segitiga PCB, siku-siku di C
$BP=\sqrt{B{{C}^{2}}+P{{C}^{2}}}$
$BP=\sqrt{{{4}^{2}}+{{2}^{2}}}=\sqrt{20}$
Perhatikan segitiga PBR, siku-siku di B
$PR=\sqrt{B{{P}^{2}}+B{{R}^{2}}}$
$PR=\sqrt{{{(\sqrt{20})}^{2}}+{{2}^{2}}}=2\sqrt{6}$
Perhatikan segitiga PQR, ternyata segitiga PQR adalah segitiga sama sisi:
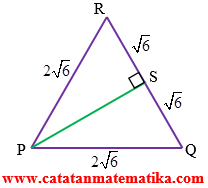
Jarak titik P ke QR adalah panjang PS:
$PS=\sqrt{P{{Q}^{2}}-Q{{S}^{2}}}$
$PS=\sqrt{{{(2\sqrt{6})}^{2}}-{{(\sqrt{6})}^{2}}}$
$PS=\sqrt{18}=3\sqrt{2}$
Jawaban: B
Matematika IPA SBMPTN 2013 No. 8
Suku banyak ${{x}^{3}}+3{{x}^{2}}+9x+3$ membagi habis ${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$ maka nilai $a+b$ adalah …
A. 12
B. 10
C. 9
D. 6
E. 3
Pembahasan:
Misalkan hasil $(x+p)$ adalah hasil pembagian ${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$ oleh ${{x}^{3}}+3{{x}^{2}}+9x+3$ maka:
Yang dibagi = pembagi x hasil + sisa
${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$$\equiv ({{x}^{3}}+3{{x}^{2}}+9x+3)(x+p)+0$
${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$$\equiv {{x}^{4}}+(p+3){{x}^{3}}+(3p+9){{x}^{2}}+(9p+3)x+3p$
$p+3=4\Leftrightarrow p=1$
$2a=3p+9\Leftrightarrow 2a=3.1+9\Leftrightarrow a=6$
$4b=9p+3\Leftrightarrow 4b=9.1+3\Leftrightarrow b=3$
$a+b=3+6=9$
Jawaban: C
Matematika IPA SBMPTN 2013 No. 9
$\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{\sin }^{2}}x-{{x}^{2}}{{\cos }^{2}}x}{x\tan x}$ = …
A. 2
B. $\frac{1}{2}$
C. -1
D. $-\frac{1}{2}$
E. -2
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{\sin }^{2}}x-{{x}^{2}}{{\cos }^{2}}x}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{\sin }^{2}}x}{x\tan x}-\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}{{\cos }^{2}}x}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{3\sin x}{x}.\frac{\sin x}{\tan x}-\underset{x\to 0}{\mathop{\lim }}\,\frac{x}{\tan x}.{{\cos }^{2}}x$
$=3.1-1.{{\cos }^{2}}{{0}^{o}}$
$=3-1$
$=2$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 10
Diketahui $f(x)=\frac{2}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-3x+\frac{1}{6}$. Jika $g(x)=f(1-2x)$, maka kurva $g$ naik pada selang …
A. $-\frac{1}{4}\le x\le 1$
B. $-1\le x\le \frac{1}{4}$
C. $-\frac{5}{4}\le x\le 1$
D. $-\frac{3}{4}\le x\le 1$
E. $\frac{3}{4}\le x\le 1$
Pembahasan:
$f(x)=\frac{2}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-3x+\frac{1}{6}$
$f'(x)=2{{x}^{2}}-x-3$
$g(x)$ naik maka $g'(x)\ge 0$
$g(x)=f(1-2x)$
$g'(x)=-2f'(1-2x)\ge 0$
$-2\left( 2{{(1-2x)}^{2}}-(1-2x)-3 \right)\ge 0$
$-2\left( 2(1-4x+4{{x}^{2}})-1+2x-3 \right)\ge 0$
$-2\left( 2-8x+8{{x}^{2}}+2x-4 \right)\ge 0$
$-2\left( 8{{x}^{2}}-6x-2 \right)\ge 0$
$-16{{x}^{2}}+12x+4\ge 0$
$4{{x}^{2}}-3x-1\le 0$
$(4x+1)(x-1)\le 0$
$-\frac{1}{4}\le x\le 1$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 11
$\int{2\cos x.\cos (1-2x)dx}$ = …
A. $\sin (x-1)+\sin (3x-1)+c$
B. $\sin (x-1)-\sin (3x-1)+c$
C. $-\sin (x-1)+\frac{1}{3}\sin (3x-1)+c$
D. $-\sin (x-1)-\frac{1}{3}\sin (3x-1)+c$
E. $\sin (x-1)+\frac{1}{3}\sin (3x-1)+c$
Pembahasan:
$\int{2\cos x.\cos (1-2x)dx}$
$=\int{\left\{ \cos (1-x)+\cos (3x-1) \right\}dx}$
$=\int{\left\{ \cos (x-1)+\cos (3x-1) \right\}dx}$
$=\sin (x-1)+\frac{1}{3}\sin (3x-1)+c$
Jawaban: E
Matematika IPA SBMPTN 2013 No. 12

Diketahui lingkaran dengan jari-jari 2, sebagaimana diberikan dalam gambar di atas. Jika tali busur pada gambar berjarak 1 dari garis tengah, maka luas daerah di bawah tali busur adalah …
A. $2\pi -2\int\limits_{0}^{1}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
B. $2\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
C. $4\pi -2\int\limits_{0}^{1}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
D. $4\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
E. $4\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}} \right)dx}$
Pembahasan:

$L=\pi {{.2}^{2}}-2\int\limits_{0}^{\sqrt{3}}{\left( {{y}_{1}}-{{y}_{2}} \right)dx}$
$L=4\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
Jawaban: D
Matematika IPA SBMPTN 2013 No. 13
Dalam kantong terdapat bola yang diberi nomor 1, 2, 3, 4 dan 5. Andi mengambil satu bola secara acak lalu mencatat nomornya dan tidak mengembalikannya. Andi melakukan pengambilan bola tersebut sebanyak tiga kali. Banyak cara Andi mendapatkan jumlah ketiga nomor bola yang diambilnya sama dengan 10 adalah …
A. 6
B. 12
C. 15
D. 16
E. 18
Pembahasan:

Banyaknya cara untuk mendapatkan jumlah ketiga angka adalah 10.
Kemunginan-kemungkinannya adalah:
Angka: 1, 4, 5 terdapat 3! = 6
Angka: 2, 3, 5 terdapat 3! = 6
Seluruhnya adalah: 6 + 6 = 12 cara.
Jawaban: B
Matematika IPA SBMPTN 2013 No. 14
Diketahui $F(x)=(1+a){{x}^{3}}-3b{{x}^{2}}-9x$ habis dibagi ${{x}^{2}}-2x+1$. Jika kurva $y=F(x)$ mempunyai titik ekstrem lokal di $(-1,F(-1))$ maka $b$ = …
A. 2
B. $\frac{6}{5}$
C. 1
D. $-\frac{6}{5}$
E. -2
Pembahasan:
$(1+a){{x}^{3}}-3b{{x}^{2}}-9x=({{x}^{2}}-2x+1).H(x)$
$(1+a){{x}^{3}}-3b{{x}^{2}}-9x=(x-1)(x-1).H(x)$
untuk $x=1$ persaman di atas menjadi:
$(1+a){{.1}^{3}}-3b{{.1}^{2}}-9.1=(1-1)(1-1).H(1)$
$1+a-3b-9=0$
$a-3b=8$ … (1)
Mempunyai ekstrim lokal di $(-1,F(-1))$ maka:
$F'(-1)=0$
$F'(x)=3(1+a){{x}^{2}}-6bx-9$
$F'(-1)=3(1+a){{(-1)}^{2}}-6b(-1)-9=0$
$3+3a+6b-9=0$
$3a+6b=6$
$a+2b=2$ …. (2)
$a-3b=8$ … (1)
-------------------- (-)
$5b=-6\Leftrightarrow b=\frac{-6}{5}$
Jawaban: D
Matematika IPA SBMPTN 2013 No. 15
Misalkan L(a) adalah luas daerah yang dibatasi oleh sumbu-X dan parabola $y=ax+{{x}^{2}}$, $0 < a < 1$. Peluang nilai $a$ sehingga $L(a)\le \frac{1}{12}$ adalah …
A. $\frac{1}{12}$
B. $\frac{1}{\sqrt{2}}$
C. $\frac{1}{\sqrt[3]{2}}$
D. $\frac{1}{6}$
E. $\frac{1}{3}$
Pembahasan:
$0 < a < 1 \Leftrightarrow n(S)=1$
$y=ax+{{x}^{2}}$
$y={{x}^{2}}+ax$
$D={{b}^{2}}-4ac={{a}^{2}}-4.1.0$
$D={{a}^{2}}$
$L=\frac{D\sqrt{D}}{{{6.1}^{2}}}$
$L=\frac{{{a}^{2}}\sqrt{{{a}^{2}}}}{6}=\frac{{{a}^{3}}}{6}$
$L(a)\le \frac{1}{12}$
$\frac{{{a}^{3}}}{6}\le \frac{1}{12}\Leftrightarrow {{a}^{3}}\le \frac{1}{2}\Leftrightarrow a\le \frac{1}{\sqrt[3]{2}}$
Jadi, $L(a)\le \frac{1}{12}$ untuk $0 < a \le \frac{1}{\sqrt[3]{2}}$, maka $n(A)=\frac{1}{\sqrt[3]{2}}$
Peluang nilai a:
$=\frac{n(A)}{n(S)}=\frac{\frac{1}{\sqrt[3]{2}}}{1}=\frac{1}{\sqrt[3]{2}}$
Jawaban: C
Matematika IPA SBMPTN 2013 No. 1
Persamaan lingkaran dengan pusat $(-1,1)$ dan menyinggung garis $3x-4y+12=0$ adalah …
A. ${{x}^{2}}+{{y}^{2}}+2x-2y+1=0$
B. ${{x}^{2}}+{{y}^{2}}+2x-2y-7=0$
C. $4{{x}^{2}}+4{{y}^{2}}+8x-8y-17=0$
D. ${{x}^{2}}+{{y}^{2}}+2x-2y-2=0$
E. $4{{x}^{2}}+4{{y}^{2}}+8x-8y-1=0$
Pembahasan:
Panjang jari-jari (r) adalah jarak titik $(-1,1)$ ke garis $3x-4y+12=0$, maka:
$r=\left| \frac{3{{x}_{1}}-4{{y}_{1}}+12}{\sqrt{{{3}^{2}}+{{4}^{2}}}} \right|$
$r=\left| \frac{3(-1)-4.1+12}{\sqrt{9+16}} \right|$
$r=1$
Persamaan lingkaran dengan pusat $(-1,1)$ dan r = 1 adalah:
${{(x+1)}^{2}}+{{(y-1)}^{2}}={{1}^{2}}$
${{x}^{2}}+2x+1+{{y}^{2}}-2y+1=1$
${{x}^{2}}+{{y}^{2}}+2x-2y+1=0$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 2
$\cot {{105}^{o}}\tan {{15}^{o}}$ = …
A. $-7+4\sqrt{3}$
B. $7+4\sqrt{3}$
C. $7-4\sqrt{3}$
D. $-7-4\sqrt{3}$
E. $-7+2\sqrt{3}$
Pembahasan:
$\cot {{105}^{o}}\tan {{15}^{o}}$
$=\cot ({{90}^{o}}+{{15}^{o}})\tan {{15}^{o}}$
$=-\tan {{15}^{o}}\tan {{15}^{o}}$
$=-{{\tan }^{2}}{{15}^{o}}$
$=-{{\tan }^{2}}({{60}^{o}}-{{45}^{o}})$
$=-{{\left( \frac{\tan {{60}^{o}}-\tan {{45}^{o}}}{1+\tan {{60}^{o}}.\tan {{45}^{o}}} \right)}^{2}}$
$=-{{\left( \frac{\sqrt{3}-1}{1+\sqrt{3}.1} \right)}^{2}}$
$=-\frac{3-2\sqrt{3}+1}{1+2\sqrt{3}+3}$
$=-\frac{4-2\sqrt{3}}{4+2\sqrt{3}}\times \frac{4-2\sqrt{3}}{4-2\sqrt{3}}$
$=-\frac{16-16\sqrt{3}+12}{16-12}$
$=-\frac{28-16\sqrt{3}}{4}$
$=-(7-4\sqrt{3})$
$=-7+4\sqrt{3}$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 3
Enam anak, 3 laki-laki dan 3 perempuan, duduk berjajar. Peluang 3 perempuan duduk berdampingan adalah …
A. $\frac{1}{60}$
B. $\frac{1}{30}$
C. $\frac{1}{15}$
D. $\frac{1}{10}$
E. $\frac{1}{5}$
Pembahasan:
Posisi duduk: LLLPPP maka $n(S)=P_{6}^{6}=6!$
A = kejadian 3 perempuan duduk berdampingan
Pertama: posisi duduk 3 perempuan = $P_{3}^{3}=3!$
Kedua: karena 3 perempuan selalu duduk berdampingan, maka kita anggap 1 tempat duduk digabung dengan 3 laki-laki, maka menjadi menyusun 4 tempat duduk yaitu: $P_{4}^{4}=4!$, maka:
$n(A)=3!.4!$
$P(A)=\frac{n(A)}{n(S)}=\frac{4!.3!}{6!}=\frac{4!.3.2.1}{6.5.4!}=\frac{1}{5}$
Jawaban: E
Matematika IPA SBMPTN 2013 No. 4
Jika dalam segitiga ABC diketahui $5\sin A+12\cos B=13$ dan $5\cos A+12\sin B=6\sqrt{2}$, maka $\sin C$ = …
A. $\frac{1}{2}$
B. $\frac{1}{2}\sqrt{2}$
C. $\frac{1}{2}\sqrt{3}$
D. $\sqrt{3}$
E. $\frac{3}{5}$
Pembahasan:
$5\sin A+12\cos B=13$, kuadratkan:
${{\left( 5\sin A+12\cos B \right)}^{2}}={{13}^{2}}$
$25{{\sin }^{2}}A+120\sin A\cos B+144{{\cos }^{2}}B=169$ … (1)
$5\cos A+12\sin B=6\sqrt{2}$, kuadratkan:
${{\left( 5\cos A+12\sin B \right)}^{2}}={{\left( 6\sqrt{2} \right)}^{2}}$
$25{{\cos }^{2}}A+120\cos A\sin B+144{{\sin }^{2}}B=72$ … (2)
Jumlahkan persamaan (1) dan (2), diperoleh:
$25{{\sin }^{2}}A$ + $25{{\cos }^{2}}A$ + $120\sin A\cos B$ +$120\cos A\sin B$ + $144{{\sin }^{2}}B$ + $144{{\cos }^{2}}B=169+72$
$25+120(\sin A\cos B$ + $\cos A\sin B)+144=241$
$120(\sin A\cos B$ + $\cos A\sin B)+169=241$
$120\sin (A+B)=72$
$\sin (A+B)=\frac{72}{120}=\frac{3}{5}$
Pada segitiga ABC:
${{180}^{o}}-C=A+B$
$\sin ({{180}^{o}}-C)=\sin (A+B)$
$\sin C=\frac{3}{5}$
Jawaban: E
Matematika IPA SBMPTN 2013 No. 5
Diketahui $(4,0,0)$, $B(0,-4,0)$, dan $C(0,0,8)$. Panjang vektor proyeksi $\overrightarrow{AC}$ ke vektor $\overrightarrow{AB}$ adalah ….
A. $2\sqrt{2}$
B. $\frac{3\sqrt{2}}{2}$
C. $\frac{\sqrt{2}}{3}$
D. $\sqrt{2}$
E. $\frac{\sqrt{3}}{2}$
Pembahasan:
$\overrightarrow{AC}=C-A$
$\overrightarrow{AC}=(0,0,8)-(4,0,0)=(-4,0,8)$
$\overrightarrow{AB}=B-A$
$\overrightarrow{AB}=(0,-4,0)-(4,0,0)=(-4,-4,0)$
Panjang vektor proyeksi $\overrightarrow{AC}$ ke vektor $\overrightarrow{AB}$:
$=\left| \frac{\overrightarrow{AC}.\overrightarrow{AB}}{|\overrightarrow{AB}|} \right|$
$=\left| \frac{(-4,0,8).(-4,-4,0)}{\sqrt{{{(-4)}^{2}}+{{(-4)}^{2}}+{{0}^{2}}}} \right|$
$=\left| \frac{16+0+0}{\sqrt{32}} \right|$
$=\frac{16}{4\sqrt{2}}$
$=2\sqrt{2}$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 6
Titik $(2a,-a)$ diputar ${{90}^{o}}$ berlawanan arah jarum jam dengan pusat perputaran titik $(2,2)$. Jika hasil rotasinya adalah $(a+4,-2)$ maka $a$ = …
A. 2
B. 1
C. 0
D. -1
E. -2
Pembahasan:
$R\left( (a,b),\theta \right)=R\left( (2,2),{{90}^{o}} \right)$
$\left( \begin{matrix} x' \\ y' \\ \end{matrix} \right)=\left( \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix} \right)\left( \begin{matrix} x-a \\ y-b \\ \end{matrix} \right)+\left( \begin{matrix} a \\ b \\ \end{matrix} \right)$
$\left( \begin{matrix} a+4 \\ -2 \\ \end{matrix} \right)=\left( \begin{matrix} \cos {{90}^{o}} & -\sin {{90}^{o}} \\ \sin {{90}^{o}} & \cos {{90}^{o}} \\ \end{matrix} \right)\left( \begin{matrix} 2a-2 \\ -a-2 \\ \end{matrix} \right)+\left( \begin{matrix} 2 \\ 2 \\ \end{matrix} \right)$
$\left( \begin{matrix} a+4 \\ -2 \\ \end{matrix} \right)-\left( \begin{matrix} 2 \\ 2 \\ \end{matrix} \right)=\left( \begin{matrix} 0 & -1 \\ 1 & 0 \\ \end{matrix} \right)\left( \begin{matrix} 2a-2 \\ -a-2 \\ \end{matrix} \right)$
$\left( \begin{matrix} a+2 \\ -4 \\ \end{matrix} \right)=\left( \begin{matrix} a+2 \\ 2a-2 \\ \end{matrix} \right)$
$2a-2=-4\Leftrightarrow a=-1$
Jawaban: D
Matematika IPA SBMPTN 2013 No. 7
Diketahui kubus ABCD.EFGH mempunyai sisi 4 cm. Titik P, adalah titik tengah CD, titik Q adalah titik tengah EH, dan titik R titik tengah BF. Jarak P ke QR adalah ….
A. $\sqrt{15}$
B. $3\sqrt{2}$
C. $\sqrt{6}$
D. $\sqrt{5}$
E. $2\sqrt{2}$
Pembahasan:
Perhatikan gambar berikut ini!

Perhatikan segitiga PCB, siku-siku di C
$BP=\sqrt{B{{C}^{2}}+P{{C}^{2}}}$
$BP=\sqrt{{{4}^{2}}+{{2}^{2}}}=\sqrt{20}$
Perhatikan segitiga PBR, siku-siku di B
$PR=\sqrt{B{{P}^{2}}+B{{R}^{2}}}$
$PR=\sqrt{{{(\sqrt{20})}^{2}}+{{2}^{2}}}=2\sqrt{6}$
Perhatikan segitiga PQR, ternyata segitiga PQR adalah segitiga sama sisi:

Jarak titik P ke QR adalah panjang PS:
$PS=\sqrt{P{{Q}^{2}}-Q{{S}^{2}}}$
$PS=\sqrt{{{(2\sqrt{6})}^{2}}-{{(\sqrt{6})}^{2}}}$
$PS=\sqrt{18}=3\sqrt{2}$
Jawaban: B
Matematika IPA SBMPTN 2013 No. 8
Suku banyak ${{x}^{3}}+3{{x}^{2}}+9x+3$ membagi habis ${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$ maka nilai $a+b$ adalah …
A. 12
B. 10
C. 9
D. 6
E. 3
Pembahasan:
Misalkan hasil $(x+p)$ adalah hasil pembagian ${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$ oleh ${{x}^{3}}+3{{x}^{2}}+9x+3$ maka:
Yang dibagi = pembagi x hasil + sisa
${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$$\equiv ({{x}^{3}}+3{{x}^{2}}+9x+3)(x+p)+0$
${{x}^{4}}+4{{x}^{3}}+2a{{x}^{2}}+4bx+c$$\equiv {{x}^{4}}+(p+3){{x}^{3}}+(3p+9){{x}^{2}}+(9p+3)x+3p$
$p+3=4\Leftrightarrow p=1$
$2a=3p+9\Leftrightarrow 2a=3.1+9\Leftrightarrow a=6$
$4b=9p+3\Leftrightarrow 4b=9.1+3\Leftrightarrow b=3$
$a+b=3+6=9$
Jawaban: C
Matematika IPA SBMPTN 2013 No. 9
$\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{\sin }^{2}}x-{{x}^{2}}{{\cos }^{2}}x}{x\tan x}$ = …
A. 2
B. $\frac{1}{2}$
C. -1
D. $-\frac{1}{2}$
E. -2
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{\sin }^{2}}x-{{x}^{2}}{{\cos }^{2}}x}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{3{{\sin }^{2}}x}{x\tan x}-\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}{{\cos }^{2}}x}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{3\sin x}{x}.\frac{\sin x}{\tan x}-\underset{x\to 0}{\mathop{\lim }}\,\frac{x}{\tan x}.{{\cos }^{2}}x$
$=3.1-1.{{\cos }^{2}}{{0}^{o}}$
$=3-1$
$=2$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 10
Diketahui $f(x)=\frac{2}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-3x+\frac{1}{6}$. Jika $g(x)=f(1-2x)$, maka kurva $g$ naik pada selang …
A. $-\frac{1}{4}\le x\le 1$
B. $-1\le x\le \frac{1}{4}$
C. $-\frac{5}{4}\le x\le 1$
D. $-\frac{3}{4}\le x\le 1$
E. $\frac{3}{4}\le x\le 1$
Pembahasan:
$f(x)=\frac{2}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-3x+\frac{1}{6}$
$f'(x)=2{{x}^{2}}-x-3$
$g(x)$ naik maka $g'(x)\ge 0$
$g(x)=f(1-2x)$
$g'(x)=-2f'(1-2x)\ge 0$
$-2\left( 2{{(1-2x)}^{2}}-(1-2x)-3 \right)\ge 0$
$-2\left( 2(1-4x+4{{x}^{2}})-1+2x-3 \right)\ge 0$
$-2\left( 2-8x+8{{x}^{2}}+2x-4 \right)\ge 0$
$-2\left( 8{{x}^{2}}-6x-2 \right)\ge 0$
$-16{{x}^{2}}+12x+4\ge 0$
$4{{x}^{2}}-3x-1\le 0$
$(4x+1)(x-1)\le 0$
$-\frac{1}{4}\le x\le 1$
Jawaban: A
Matematika IPA SBMPTN 2013 No. 11
$\int{2\cos x.\cos (1-2x)dx}$ = …
A. $\sin (x-1)+\sin (3x-1)+c$
B. $\sin (x-1)-\sin (3x-1)+c$
C. $-\sin (x-1)+\frac{1}{3}\sin (3x-1)+c$
D. $-\sin (x-1)-\frac{1}{3}\sin (3x-1)+c$
E. $\sin (x-1)+\frac{1}{3}\sin (3x-1)+c$
Pembahasan:
$\int{2\cos x.\cos (1-2x)dx}$
$=\int{\left\{ \cos (1-x)+\cos (3x-1) \right\}dx}$
$=\int{\left\{ \cos (x-1)+\cos (3x-1) \right\}dx}$
$=\sin (x-1)+\frac{1}{3}\sin (3x-1)+c$
Jawaban: E
Matematika IPA SBMPTN 2013 No. 12

Diketahui lingkaran dengan jari-jari 2, sebagaimana diberikan dalam gambar di atas. Jika tali busur pada gambar berjarak 1 dari garis tengah, maka luas daerah di bawah tali busur adalah …
A. $2\pi -2\int\limits_{0}^{1}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
B. $2\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
C. $4\pi -2\int\limits_{0}^{1}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
D. $4\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
E. $4\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}} \right)dx}$
Pembahasan:

$L=\pi {{.2}^{2}}-2\int\limits_{0}^{\sqrt{3}}{\left( {{y}_{1}}-{{y}_{2}} \right)dx}$
$L=4\pi -2\int\limits_{0}^{\sqrt{3}}{\left( \sqrt{4-{{x}^{2}}}-1 \right)dx}$
Jawaban: D
Matematika IPA SBMPTN 2013 No. 13
Dalam kantong terdapat bola yang diberi nomor 1, 2, 3, 4 dan 5. Andi mengambil satu bola secara acak lalu mencatat nomornya dan tidak mengembalikannya. Andi melakukan pengambilan bola tersebut sebanyak tiga kali. Banyak cara Andi mendapatkan jumlah ketiga nomor bola yang diambilnya sama dengan 10 adalah …
A. 6
B. 12
C. 15
D. 16
E. 18
Pembahasan:

Banyaknya cara untuk mendapatkan jumlah ketiga angka adalah 10.
Kemunginan-kemungkinannya adalah:
Angka: 1, 4, 5 terdapat 3! = 6
Angka: 2, 3, 5 terdapat 3! = 6
Seluruhnya adalah: 6 + 6 = 12 cara.
Jawaban: B
Matematika IPA SBMPTN 2013 No. 14
Diketahui $F(x)=(1+a){{x}^{3}}-3b{{x}^{2}}-9x$ habis dibagi ${{x}^{2}}-2x+1$. Jika kurva $y=F(x)$ mempunyai titik ekstrem lokal di $(-1,F(-1))$ maka $b$ = …
A. 2
B. $\frac{6}{5}$
C. 1
D. $-\frac{6}{5}$
E. -2
Pembahasan:
$(1+a){{x}^{3}}-3b{{x}^{2}}-9x=({{x}^{2}}-2x+1).H(x)$
$(1+a){{x}^{3}}-3b{{x}^{2}}-9x=(x-1)(x-1).H(x)$
untuk $x=1$ persaman di atas menjadi:
$(1+a){{.1}^{3}}-3b{{.1}^{2}}-9.1=(1-1)(1-1).H(1)$
$1+a-3b-9=0$
$a-3b=8$ … (1)
Mempunyai ekstrim lokal di $(-1,F(-1))$ maka:
$F'(-1)=0$
$F'(x)=3(1+a){{x}^{2}}-6bx-9$
$F'(-1)=3(1+a){{(-1)}^{2}}-6b(-1)-9=0$
$3+3a+6b-9=0$
$3a+6b=6$
$a+2b=2$ …. (2)
$a-3b=8$ … (1)
-------------------- (-)
$5b=-6\Leftrightarrow b=\frac{-6}{5}$
Jawaban: D
Matematika IPA SBMPTN 2013 No. 15
Misalkan L(a) adalah luas daerah yang dibatasi oleh sumbu-X dan parabola $y=ax+{{x}^{2}}$, $0 < a < 1$. Peluang nilai $a$ sehingga $L(a)\le \frac{1}{12}$ adalah …
A. $\frac{1}{12}$
B. $\frac{1}{\sqrt{2}}$
C. $\frac{1}{\sqrt[3]{2}}$
D. $\frac{1}{6}$
E. $\frac{1}{3}$
Pembahasan:
$0 < a < 1 \Leftrightarrow n(S)=1$
$y=ax+{{x}^{2}}$
$y={{x}^{2}}+ax$
$D={{b}^{2}}-4ac={{a}^{2}}-4.1.0$
$D={{a}^{2}}$
$L=\frac{D\sqrt{D}}{{{6.1}^{2}}}$
$L=\frac{{{a}^{2}}\sqrt{{{a}^{2}}}}{6}=\frac{{{a}^{3}}}{6}$
$L(a)\le \frac{1}{12}$
$\frac{{{a}^{3}}}{6}\le \frac{1}{12}\Leftrightarrow {{a}^{3}}\le \frac{1}{2}\Leftrightarrow a\le \frac{1}{\sqrt[3]{2}}$
Jadi, $L(a)\le \frac{1}{12}$ untuk $0 < a \le \frac{1}{\sqrt[3]{2}}$, maka $n(A)=\frac{1}{\sqrt[3]{2}}$
Peluang nilai a:
$=\frac{n(A)}{n(S)}=\frac{\frac{1}{\sqrt[3]{2}}}{1}=\frac{1}{\sqrt[3]{2}}$
Jawaban: C
Artikel Terkait:
|

Post a Comment for "Pembahasan Matematika IPA SBMPTN Tahun 2013 Kode 135"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.