Pembahasan SBMPTN 2015 Matematika IPA
SBMPTN (Seleksi Bersama Masuk Perguruan Tinggi Negeri) akan segera dimulai. Mengingat begitu banyaknya minat siswa-siswi SMA Kelas 12 ingin melanjutkan pendidikan dengan kuliah di perguruan tinggi negeri, tentu akan semakin meningkatkan daya saing untuk bisa lolos SBMPTN. Untuk itu, perlu bagi adik-adik pejuang SBMPTN, terlebih yang kurang beruntung mendapatkan tiket SNMPTN yaitu tiket seleksi masuk PTN melalui jalur undangan untuk mempersiapkan diri secara matang. Ingat, pesaingmu sedang belajar sekarang, dan cara belajarmu harus melebihi cara belajar pesaingmu. Catatan Matematika kembali membagikan bahan belajar yaitu Soal dan Pembahasan Matematika IPA SBMPTN 2015 (untuk soalnya tersedia dalam bentuk file pdf yang dapat kalian download dan print, link download tersedia di bawah ini).
Matematika IPA SBMPTN 2015 No. 1
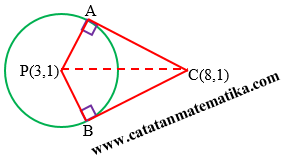
Misalkan titik A dan B pada lingkaran ${{x}^{2}}+{{y}^{2}}-6x-2y+k=0$ sehingga garis singgung lingkaran di titik A dan B berpotongan di C(8,1). Jika luas segiempat yang melalui A, B, C, dan pusat lingkaran adalah 12, maka k = ….
A. -1
B. 0
C. 1
D. 2
E. 3
Pembahasan:
${{x}^{2}}+{{y}^{2}}-6x-2y+k=0$,
A = -6, B = -2, C = k
Titik pusat lingkaran:
$P\left( \frac{A}{-2},\frac{B}{-2} \right)=P\left( \frac{-6}{-2},\frac{-2}{-2} \right)=P\left( 3,1 \right)$
Perhatikan sketsa gambar berikut:
PC = $\sqrt{{{(8-3)}^{2}}+{{(1-1)}^{2}}}=5$
Luas ACBP = 12, luas segitiga PAC = luas segitiga PBC = 6.
Misal: AC = s, AP = r, maka:
$\frac{1}{2}.AP.AC=6$
$\frac{1}{2}.r.s=6\Leftrightarrow rs=12$
Berdasarkan teorema phytagoras:
$A{{P}^{2}}+A{{C}^{2}}=P{{C}^{2}}$
${{r}^{2}}+{{s}^{2}}={{5}^{2}}$
${{r}^{2}}+{{\left( \frac{12}{r} \right)}^{2}}=25$
${{r}^{2}}+\frac{144}{{{r}^{2}}}=25$
${{r}^{4}}-25{{r}^{2}}+144=0$
$({{r}^{2}}-9)({{r}^{2}}-16)=0$
$r=3$ atau $r=4$
Pilih r = 3,
$r=\sqrt{\frac{{{A}^{2}}+{{B}^{2}}-4C}{4}}$
${{r}^{2}}=\frac{{{A}^{2}}+{{B}^{2}}-4C}{4}$
${{3}^{2}}=\frac{{{(-6)}^{2}}+{{(-2)}^{2}}-4k}{4}$
$36=36+4-4k\Leftrightarrow k=1$
Jawaban: C
Matematika IPA SBMPTN 2015 No. 2
Jika $\cos (x+{{15}^{o}})=a$ dengan ${{0}^{o}}\le x\le {{30}^{o}}$, maka nilai $\cos (2x+{{60}^{o}})$ adalah …
A. $\frac{\sqrt{3}}{2}\left( 2{{a}^{2}}-1 \right)+a\sqrt{1-{{a}^{2}}}$
B. $\frac{\sqrt{3}}{2}\left( 2{{a}^{2}}-1 \right)-a\sqrt{1-{{a}^{2}}}$
C. $\frac{\sqrt{3}}{2}\left( {{a}^{2}}-1 \right)-a\sqrt{1-{{a}^{2}}}$
D. $\frac{\sqrt{3}}{2}\left( 2{{a}^{2}}-1 \right)-a\sqrt{1+{{a}^{2}}}$
E. $\frac{\sqrt{3}}{2}\left( {{a}^{2}}+1 \right)+a\sqrt{1-{{a}^{2}}}$
Pembahasan:
$\cos (x+{{15}^{o}})=a$
$\frac{sa}{mi}=\frac{a}{1}\Rightarrow de=\sqrt{1-{{a}^{2}}}$
$\cos (2x+{{60}^{o}})$
= $\cos \left[ 2(x+{{15}^{o}})+{{30}^{o}} \right]$
= $\cos 2(x+{{15}^{o}}).\cos {{30}^{o}}$ - $\sin 2(x+{{15}^{o}}).\sin {{30}^{o}}$
= $\left( 2{{\cos }^{2}}(x+{{15}^{o}})-1 \right).\frac{1}{2}\sqrt{3}$ - $2\sin (x+{{15}^{o}}).\cos (x+{{15}^{o}}).\frac{1}{2}$
= $\left( 2{{a}^{2}}-1 \right).\frac{1}{2}\sqrt{3}-\sqrt{1-{{a}^{2}}}.a$
= $\frac{\sqrt{3}}{2}\left( 2{{a}^{2}}-1 \right)-a\sqrt{1-{{a}^{2}}}$
Jawaban: B
Matematika IPA SBMPTN 2015 No. 3
Misalkan $|\overrightarrow{OA}|=4$, $|\overrightarrow{OB}|=3$ dan kuadrat luas $\Delta ABO=27$, maka sudut kedua vektor adalah …
A. ${{70}^{o}}$
B. ${{60}^{o}}$
C. ${{45}^{o}}$
D. ${{30}^{o}}$
E. ${{15}^{o}}$
Pembahasan:
kuadrat luas $\Delta ABO=27$, maka:
luas $\Delta ABO=\sqrt{27}$
$\frac{1}{2}.|OA|.|OB|.\sin \angle (OA,OB)=\sqrt{27}$
$\frac{1}{2}.4.3.\sin \angle (OA,OB)=3\sqrt{3}$
$\sin \angle (OA,OB)=\frac{1}{2}\sqrt{3}$
$\angle (OA,OB)={{60}^{o}}$
Jawaban: B
Matematika IPA SBMPTN 2015 No. 4
Pencerminan garis $y=-x+2$ terhadap garis y = 3 menghasilkan …
A. y = x + 4
B. y = -x + 4
C. y = x + 2
D. y = x – 2
E. y = -x – 4
Pembahasan:
$P(x,y)\xrightarrow{y=3}P'(x,2.3-y)$
$P'(x,6-y)=P'(x',y')$
$x=x'$ dan $6-y=y'\Leftrightarrow y=6-y'$
Substitusi ke persamaan garis:
$y=-x+2$
$6-y'=-x'+2$
$-y'=-x'-4$
$y'=x'+4$
Jawaban: A
Matematika IPA SBMPTN 2015 No. 5
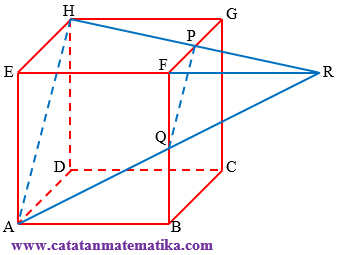
Pada kubus ABCD.EFGH, titik P adalah titik tengah FG dan titik Q adalah titik tengah FB. Perpanjangan HP dan AQ berpotongan di perpanjangan EF di titik R. Jika panjang rusuk kubus adalah 2, maka volume EAH.FQP adalah …
A. 3
B. 2
C. $3\frac{1}{3}$
D. $2\frac{1}{3}$
E. $2\frac{2}{3}$
Pembahasan:
$\Delta AER$ sebangun dengan $\Delta QFR$maka:
$\frac{AE}{QF}=\frac{ER}{FR}$
$\frac{2}{1}=\frac{2+FR}{FR}$
$2FR=2+FR\Leftrightarrow FR=2$
${{V}_{EAH.FQP}}={{V}_{EAH.R}}-{{V}_{FQP.R}}$
$=\frac{1}{3}.\left( \frac{1}{2}.AE.EH \right).ER-\frac{1}{3}.\left( \frac{1}{2}.FQ.FP \right).FR$
$=\frac{1}{3}.\left( \frac{1}{2}.2.2 \right).4-\frac{1}{3}.\left( \frac{1}{2}.1.1 \right).2$
$=\frac{8}{3}-\frac{1}{3}=\frac{7}{3}=2\frac{1}{3}$
Jawaban: D
Matematika IPA SBMPTN 2015 No. 6
Suku banyak $p(x)={{(x-a)}^{5}}+{{(x-b)}^{4}}+(x-c)$ habis dibagi oleh ${{x}^{2}}-(a+b)x+ab$. Jika $a-c\ne 1$, maka b = …
A. $\frac{c-ac+{{a}^{2}}}{c+1-a}$
B. $\frac{{{c}^{2}}+ac-a}{c+1-a}$
C. $\frac{c+2ac-{{a}^{2}}}{c+1-a}$
D. $\frac{2{{c}^{2}}+ac-{{a}^{2}}}{c+1-a}$
E. $\frac{c+ac-{{a}^{2}}}{c+1-a}$
Pembahasan:
Habis dibagi berarti sisa = 0
$p(x)={{(x-a)}^{5}}+{{(x-b)}^{4}}+(x-c)$
Pembagi:
${{x}^{2}}-(a+b)x+ab=(x-a)(x-b)$
$p(a)=0$
${{(a-a)}^{5}}+{{(a-b)}^{4}}+(a-c)=0$
${{(a-b)}^{4}}=c-a$ … persamaan (1)
$p(b)=0$
${{(b-a)}^{5}}+{{(b-b)}^{4}}+(b-c)=0$
${{(b-a)}^{5}}=c-b$ … persamaan (2)
Persamaan (2) dibagi dengan persamaan (1):
$\frac{{{(b-a)}^{5}}}{{{(a-b)}^{4}}}=\frac{c-b}{c-a}$
$\frac{{{(b-a)}^{5}}}{{{(b-a)}^{4}}}=\frac{c-b}{c-a}$
$b-a=\frac{c-b}{c-a}$
$bc-ab-ac+{{a}^{2}}=c-b$
$bc-ab+b=c+ac-{{a}^{2}}$
$b(c-a+1)=c+ac-{{a}^{2}}$
$b=\frac{c+ac-{{a}^{2}}}{c+1-a}$
Jawaban: E
Matematika IPA SBMPTN 2015 No. 7
Nilai c yang memenuhi: ${{(0,25)}^{(-{{x}^{2}}+4x-c)}} < {{(0,0625)}^{(-{{x}^{2}}-4x+5)}}$ adalah …
A. c < -46
B. c < -33
C. c < -23
D. c < 23
E. c < 46
Pembahasan:
${{(0,25)}^{(-{{x}^{2}}+4x-c)}} < {{(0,0625)}^{(-{{x}^{2}}-4x+5)}}$
${{(0,25)}^{(-{{x}^{2}}+4x-c)}} < {{(0,25)}^{2(-{{x}^{2}}-4x+5)}}$
$-{{x}^{2}}+4x-c > -2{{x}^{2}}-8x+10$
${{x}^{2}}+12x-c-10 > 0$ (definit positif)
D < 0
${{12}^{2}}-4.1.(-c-10) < 0$
$144+4c+40 < 0$
$4c < -184 \Leftrightarrow c < -46$
Jawaban: A
Matematika IPA SBMPTN 2015 No. 8
Jika ${{x}_{1}},{{x}_{2}}$ adalah akar-akar ${{16}^{x}}-{{4}^{x}}-{{2.4}^{x+2}}-{{4}^{x+3}}+a=0$ dimana ${{x}_{1}}+{{x}_{2}}{{=}^{2}}\log 5+1$, maka a = …
A. 16
B. 18
C. 25
D. 64
E. 100
Pembahasan:
${{16}^{x}}-{{4}^{x}}-{{2.4}^{x+2}}-{{4}^{x+3}}+a=0$
${{({{4}^{x}})}^{2}}-{{4}^{x}}-{{2.4}^{2}}{{.4}^{x}}-{{4}^{3}}{{.4}^{x}}+a=0$
${{({{4}^{x}})}^{2}}-{{4}^{x}}-{{32.4}^{x}}-{{64.4}^{x}}+a=0$
${{({{4}^{x}})}^{2}}-{{97.4}^{x}}+a=0$ akar-akarnya ${{4}^{{{x}_{1}}}}$ dan ${{4}^{{{x}_{2}}}}$
${{4}^{{{x}_{1}}}}{{.4}^{{{x}_{2}}}}=a$
${{4}^{{{x}_{1}}+{{x}_{2}}}}=a$
${{x}_{1}}+{{x}_{2}}{{=}^{4}}\log a{{=}^{2}}\log 5+1$
$^{2}\log {{a}^{\frac{1}{2}}}{{=}^{2}}\log 5{{+}^{2}}\log 2$
$^{2}\log \sqrt{a}{{=}^{2}}\log 10$
$\sqrt{a}=10\Leftrightarrow a=100$
Jawaban: E
Matematika IPA SBMPTN 2015 No. 9
Nilai $\underset{x\to 1}{\mathop{\lim }}\,\frac{\left( \sqrt{5-x}-2 \right)\left( \sqrt{2-x}+1 \right)}{1-x}$ adalah …
A. $-\frac{1}{2}$
B. $-\frac{1}{4}$
C. $\frac{1}{8}$
D. $\frac{1}{4}$
E. $\frac{1}{2}$
Pembahasan:
$\underset{x\to 1}{\mathop{\lim }}\,\frac{\left( \sqrt{5-x}-2 \right)\left( \sqrt{2-x}+1 \right)}{1-x}$
= $\underset{x\to 1}{\mathop{\lim }}\,\frac{\left( \sqrt{5-x}-2 \right)}{1-x}$. $\underset{x\to 1}{\mathop{\lim }}\,\left( \sqrt{2-x}+1 \right)$
= $\underset{x\to 1}{\mathop{\lim }}\,\frac{\left( \sqrt{5-x}-2 \right)}{1-x}.\frac{\left( \sqrt{5-x}+2 \right)}{\left( \sqrt{5-x}+2 \right)}$. $\left( \sqrt{2-1}+1 \right)$
= $\underset{x\to 1}{\mathop{\lim }}\,\frac{5-x-4}{(1-x)\left( \sqrt{5-x}+2 \right)}$. 2
= $\underset{x\to 1}{\mathop{\lim }}\,\frac{(1-x).2}{(1-x)\left( \sqrt{5-x}+2 \right)}$
= $\underset{x\to 1}{\mathop{\lim }}\,\frac{2}{\left( \sqrt{5-x}+2 \right)}$
= $\frac{2}{\left( \sqrt{5-1}+2 \right)}=\frac{1}{2}$
Jawaban: E
Matematika IPA SBMPTN 2015 No. 10
Jika ${{u}_{1}},{{u}_{2}},{{u}_{3}},$… adalah barisan geometri yang memenuhi ${{u}_{3}}-{{u}_{6}}=x$ dan ${{u}_{2}}-{{u}_{4}}=y$, maka $\frac{x}{y}$ = …
A. $\frac{{{r}^{3}}-{{r}^{2}}-r}{r-1}$
B. $\frac{{{r}^{3}}-{{r}^{2}}+r}{r-1}$
C. $\frac{{{r}^{3}}+{{r}^{2}}+r}{r+1}$
D. $\frac{{{r}^{3}}+{{r}^{2}}-r}{r-1}$
E. $\frac{{{r}^{3}}-{{r}^{2}}+r}{r+1}$
Pembahasan:
$\frac{x}{y}=\frac{{{u}_{3}}-{{u}_{6}}}{{{u}_{2}}-{{u}_{4}}}$
$\frac{x}{y}=\frac{a{{r}^{2}}-a{{r}^{5}}}{ar-a{{r}^{3}}}$
$\frac{x}{y}=\frac{ar(r-{{r}^{4}})}{ar(1-{{r}^{2}})}$
$\frac{x}{y}=\frac{r(1-r)({{r}^{2}}+r+1)}{(1-r)(1+r)}$
$\frac{x}{y}=\frac{{{r}^{3}}+{{r}^{2}}+r}{1+r}$
Jawaban: C
Matematika IPA SBMPTN 2015 No. 11
Fungsi $f(x)=-\sqrt{{{\cos }^{2}}x+\frac{x}{2}+\pi }$, $-\pi < x < 2\pi $ turun pada interval …
A. $0 < x < \frac{5\pi }{12}$
B. $0 < x < \frac{\pi }{12}$
C. $\frac{\pi }{6} < x < \frac{\pi }{3}$
D. $\frac{5\pi }{12} < x < \frac{7\pi }{12}$
E. $-\frac{7\pi }{12} < x < \frac{\pi }{12}$
Pembahasan:
$f(x)=-\sqrt{{{\cos }^{2}}x+\frac{x}{2}+\pi }$ turun maka $f'(x) < 0$
$f'(x)=-\frac{2.\cos x.(-\sin x)+\frac{1}{2}}{\sqrt{{{\cos }^{2}}x+\frac{x}{2}+\pi }}$
$\frac{\sin 2x-\frac{1}{2}}{2\sqrt{{{\cos }^{2}}x+\frac{x}{2}+\pi }} < 0$
$\sin 2x-\frac{1}{2} < 0 \Leftrightarrow \sin 2x < \frac{1}{2}$
HP = {$\frac{-7\pi }{12} < x < \frac{\pi }{12}$}
Jawaban: E
Matematika IPA SBMPTN 2015 No. 12
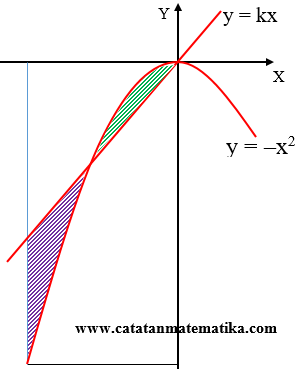
Pada interval $-10\le x\le 0$, luas daerah di bawah kurva $y=-{{x}^{2}}$ dan di atas $y=kx$ sama dengan luas daerah di atas kurva $y=-{{x}^{2}}$ dan di bawah garis $y=kx$. Nilai k = …
A. $7\frac{1}{3}$
B. $6\frac{2}{3}$
C. 6
D. $5\frac{2}{3}$
E. 5
Pembahasan:
Titik potong $y=kx$ dan $y=-{{x}^{2}}$
$kx=-{{x}^{2}}$
${{x}^{2}}+kx=0$
$x(x+k)=0$
$x=-k$ atau $x=0$
Luas biru = Luas hijau
$\int\limits_{-10}^{-k}{\left( kx-(-{{x}^{2}}) \right)dx}=\int\limits_{-k}^{0}{\left( -{{x}^{2}}-kx \right)}dx$
$\left. \frac{k}{2}{{x}^{2}}+\frac{1}{3}{{x}^{3}} \right|_{-10}^{-k}=\left. -\frac{1}{3}{{x}^{3}}-\frac{k}{2}{{x}^{2}} \right|_{-k}^{0}$
$\left( \frac{k}{2}{{(-k)}^{2}}+\frac{1}{3}{{(-k)}^{3}} \right)-\left( \frac{k}{2}{{(-10)}^{2}}+\frac{1}{3}{{(-10)}^{3}} \right)$ = $\left( -\frac{1}{3}{{.0}^{3}}-\frac{k}{2}{{.0}^{2}} \right)-\left( -\frac{1}{3}{{(-k)}^{3}}-\frac{k}{2}{{(-k)}^{2}} \right)$
$\left( \frac{{{k}^{3}}}{2}-\frac{{{k}^{3}}}{3} \right)-\left( \frac{100k}{2}-\frac{1000}{3} \right)$ = $0-\left( \frac{{{k}^{3}}}{3}-\frac{{{k}^{3}}}{2} \right)$
$-\frac{{{k}^{3}}}{3}+\frac{{{k}^{3}}}{2}-50k+\frac{1000}{3}$ = $-\frac{{{k}^{3}}}{3}+\frac{{{k}^{3}}}{2}$
$-50k=-\frac{1000}{3}$
$k=\frac{20}{3}\Leftrightarrow k=6\frac{2}{3}$
Jawaban: B
Matematika IPA SBMPTN 2015 No. 13
Banyak garis lurus $Ax+By-4C=0$ dengan A, B, dan C bilangan-bilangan berbeda yang dipilih dari {0, 1, 4, 16} adalah …
A. 9
B. 12
C. 15
D. 18
E. 21
Pembahasan:
$Ax+By-4C=0$
$A,B,C\in \{0,1,4,16\}$ maka banyak garis lurus adalah 4 x 3 x 2 = 24 garis
Ternyata:
*) Jika A = 0, B = 4, C = 1 sama dengan A = 0, B = 16, C = 4 persamaan garisnya 4y – 4 = 0.
*) Jika A = 4, B = 0, C = 1 sama dengan A = 16, B = 0, C = 4 persamaan garisnya 4x – 4 = 0
*) Jika A = 1, B = 4, C = 0 sama dengan A = 4, B = 16, C = 0 persamaan garisnya 4x + 16 = 0
Jadi, banyak garis lurus $Ax+By-4C=0$ yang berbeda adalah 24 – 3 = 21 garis.
Jawaban: E
Matematika IPA SBMPTN 2015 No. 14
Dua kelas masing-masing terdiri atas 30 siswa. Satu siswa dipilih dari tiap-tiap kelas. Peluang terpilih keduanya laki-laki adalah $\frac{11}{36}$. Peluang terpilih paling sedikit satu di antaranya laki-laki adalah …
A. $\frac{161}{180}$
B. $\frac{155}{180}$
C. $\frac{25}{180}$
D. $\frac{19}{180}$
E. $\frac{11}{180}$
Pembahasan:
Misal:
x = banyak laki-laki di kelas A
y = banyak laki-laki di kelas B
Peluang terpilih laki-laki dari kelas A dan kelas B adalah:
$\frac{x}{30}\times \frac{y}{30}=\frac{11}{36}\Leftrightarrow x.y=25\times 11$
Artinya, x = 25 = banyak laki-laki di kelas A, y = 11 = banyak laki-laki di kelas B.
Peluang paling sedikit satu laki-laki = komplemen peluang terpilih keduanya perempuan.
= $1-\frac{5}{30}\times \frac{19}{30}=\frac{161}{180}$
Jawaban: A
Matematika IPA SBMPTN 2015 No. 15
Diketahui deret geometri tak hingga mempunyai jumlah sama dengan nilai minimum fungsi $f(x)=-{{x}^{3}}+3x-c$ untuk $-1\le x\le 2$. Selisih suku kedua dan suku pertama deret geometri tersebut adalah $f'(0)$. Jika rasio deret geometri tersebut $1-\sqrt{3}$, maka nilai c adalah …
A. -2
B. -1
C. 1
D. 2
E. 3
Pembahasan:
$f(x)=-{{x}^{3}}+3x-c$
$f'(x)=-3{{x}^{2}}+3$, nilai minimum diperoleh untuk $x=-1$
${{S}_{\infty }}=f(-1)$
${{S}_{\infty }}=-{{(-1)}^{3}}+3(-1)-c$
${{S}_{\infty }}=-2-c$
Deret Geometri: $r=1-\sqrt{3}$
${{U}_{2}}-{{U}_{1}}=f'(0)$
$ar-a=-{{3.0}^{2}}+3$
$a(1-\sqrt{3})-a=3$
$a-a\sqrt{3}-a=3$
$-a\sqrt{3}=3\Leftrightarrow a=-\sqrt{3}$
${{S}_{\infty }}=\frac{a}{1-r}$
$-2-c=\frac{-\sqrt{3}}{1-(1-\sqrt{3})}$
$-2-c=-1\Leftrightarrow c=-1$
Jawaban: B
Artikel Terkait:
|
Semoga postingan: Pembahasan SBMPTN 2015 Matematika IPA ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Pembahasan SBMPTN 2015 Matematika IPA"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.