Pembahasan SBMPTN 2015 Matematika Dasar
Yuk belajar lagi hal-hal dasar dan sederhana yaitu TKPA (Tes Kemampuan Potensi Akademik), Matematika Dasar. Pembahasan kali ini adalah Matematika Dasar SBMPTN 2015 Kode 623. Sebaiknya downloadlah soalnya terlebih dahulu agar dapat dipelajari secara mandiri. Nih link downloadnya.
#Selamat belajar...! Semoga kalian lulus dan menjadi salah satu mahasiswa di PTN (Perguruan Tinggi Negeri).
Matematika Dasar SBMPTN 2015 No. 1
Diketahui $a$ dan $b$ adalah bilangan real positif. Jika $\frac{(a-\sqrt{b})\sqrt{b}+(a-\sqrt{b})a}{{{a}^{2}}-b}=c$, maka nilai $c$ adalah …
A. $a-\sqrt{b}$
B. ${{a}^{2}}-b$
C. 0
D. 1
E. 2
Pembahasan:
$\frac{(a-\sqrt{b})\sqrt{b}+(a-\sqrt{b})a}{{{a}^{2}}-b}=c$
$\frac{(a-\sqrt{b})(\sqrt{b}+a)}{(a-\sqrt{b})(a+\sqrt{b})}=c$
$1=c$
Jawaban: D
Matematika Dasar SBMPTN 2015 No. 2
Diketahui suatu barisan aritmetika dengan suku pertama dan suku ketiga berturut-turut adalah $k-1$ dan $3k+1$. Jika suku kesepuluh adalah 98, maka suku kelima barisan tersebut adalah …
A. 58 B. 56 C. 48 D. 46 E. 36
Pembahasan:
Barisan Aritmetika: ${{U}_{n}}=a+(n-1)b$
$a=k-1$
${{U}_{3}}=3k+1$
$a+2b=3k+1$
$k-1+2b=3k+1$
$2b=2k+2\Rightarrow b=k+1$
${{U}_{10}}=98$
$a+9b=98$
$k-1+9(k+1)=98$
$10k=90\Leftrightarrow k=9$
$a=k-1\Leftrightarrow a=9-1=8$
$b=k+1\Leftrightarrow b=9+1=10$
${{U}_{5}}=a+4b=8+4.10=48$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 3
Diketahui persegi panjang ABCD. Jika panjang BE = panjang EF = panjang FC = 5 cm dan panjang DG = panjang GH = panjang HC = 3 cm, maka luas daerah yang diarsir adalah … $c{{m}^{2}}$.

A. 22,5
B. 45
C. 60
D. 67,5
E. 90
Pembahasan:
AB = DG + GH + HC = 9 cm
AD = BE + EF + FC = 15 cm
Luas segitiga AEF:
$=\frac{EF\times AB}{2}=\frac{5\times 9}{2}=\frac{45}{2}$
Luas segitiga AGH:
$=\frac{GH\times AD}{2}=\frac{3\times 15}{2}=\frac{45}{2}$
Luas arsiran $=\frac{45}{2}+\frac{45}{2}=45$
Jawaban: B
Matematika Dasar SBMPTN 2015 No. 4
Jika $^{a}\log 2=x$ dan $^{a}\log 5=y$, maka $\log {{a}^{3x}}+3\log {{a}^{y}}$ = …
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
$^{a}\log 2=x\Leftrightarrow {{a}^{x}}=2$
$^{a}\log 5=y\Leftrightarrow {{a}^{y}}=5$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{\left( {{a}^{x}} \right)}^{3}}+\log {{\left( {{a}^{y}} \right)}^{3}}$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{2}^{3}}+\log {{5}^{3}}$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{(2.5)}^{3}}$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{10}^{3}}=3$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 5
Diagram berikut ini menyajikan data (dalam bilangan bulat) nilai sementara dan nilai ujian ulang mahasiswa peserta kuliah Matematika.
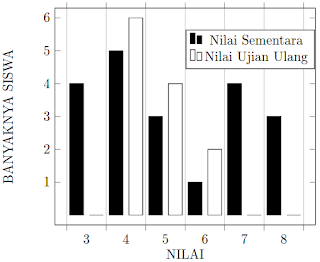
Ujian ulang diikuti hanya oleh peserta kuliah tersebut dengan nilai sementara lebih kecil daripada 6. Jika yang dinyatakan lulus adalah mahasiswa yang memperoleh nilai sementara tidak lebih kecil daripada 6 atau nilai ujian ulangnya adalah 6, maka rata-rata nilai mahasiswa yang lulus mata kuliah tersebut adalah …
A. 6,33
B. 6,50
C. 6,75
D. 7,00
E. 7,25
Pembahasan:
Syarat lulus: nilai sementara tidak lebih kecil daripada 6 atau nilai ujian ulangnya 6
Yang lulus berdasarkan nilai sementara:
Nilai 6 ada 1 orang.
Nilai 7 ada 4 orang.
Nilai 8 ada 3 orang.
Yang lulus berdasarkan nilai ujian ulang.
Nilai 6 ada 2 orang.
$\bar{x}=\frac{6.1+7.4+8.3+6.2}{1+4+3+2}=7,00$
Jawaban: D
Matematika Dasar SBMPTN 2015 No. 6
Himpunan penyelesaian pertidaksamaan $\frac{x-1}{x} < 2$ adalah …
A. {$x\in R|x > 0$}
B. {$x\in R|x > -1$}
C. {$x\in R|x < -1$}
D. {$x\in R|x < -1$ atau $x > 0$}
E. {$x\in R|x < 0$ atau $x > 1$}
Pembahasan:
$\frac{x-1}{x} < 2$
$\frac{x-1}{x}-2 < 0 $
$\frac{x-1}{x}-\frac{2x}{x} < 0$
$\frac{-x-1}{x} < 0$
$(-x-1)x < 0$
$(x+1)x > 0$
$x < -1$ atau $x > 0$
Jawaban: D
Matematika Dasar SBMPTN 2015 No. 7
Diketahui suatu fungsi $f$ bersifat $f(-x)=-f(x)$ untuk setiap bilangan real $x$. Jika $f(3)=-5$ dan $f(-5)=1$, maka $f(f(-3))$ = …
A. -5 B. -2 C. -1 D. 1 E. 2
Pembahasan:
$f(f(-3))=f(-f(3))$
$f(f(-3))=f(-(-5))$
$f(f(-3))=f(5)$
$f(-x)=-f(x)\Leftrightarrow f(x)=-f(-x)$
$f(5)=-f(-5)$
$f(5)=-1$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 8
Diketahui sistem persamaan linear
$\frac{2x+1}{3}-\frac{2-3y}{2}=3$
$\frac{4x+y}{6}+\frac{x+y}{3}=2$
Nilai $x+y$ adalah …
A. -3 B. -2 C. 1 D. 2 E. 3
Pembahasan:
$\frac{2x+1}{3}-\frac{2-3y}{2}=3$ kedua ruas kali 6,
$2(2x+1)-3(2-3y)=18$
$4x+9y=22$ …. Persamaan 1
$\frac{4x+y}{6}+\frac{x+y}{3}=2$ kedua ruas kali 6,
$4x+y+2(x+y)=12$
$6x+3y=12$, kalikan dengan 3
$18x+9y=36$ … persamaan 2
$4x+9y=22$ …. Persamaan 1
------------------------------------- (-)
$14x=14\Leftrightarrow x=1$
$4.1+9y=22\Leftrightarrow y=2$
$x+y=1+2=3$
Jawaban: E
Matematika Dasar SBMPTN 2015 No. 9
Empat orang siswa akan mengikuti suatu perlombaan karya inovatif. Untuk itu, diperlukan biaya Rp 900.000,-. Karena masing-masing memiliki kondisi keuangan yang berbeda, besar kontribusi masing-masing siswa tidak sama. Siswa A memberikan kontribusi setengah dari jumlah kontribusi tiga siswa lainnya. Siswa B memberikan kontribusi sepertiga dari jumlah kontribusi tiga siswa lainnya. Siswa C memberikan kontribusi seperempat dari jumlah kontribusi tiga siswa lainnya. Besar kontribusi siswa D adalah Rp . . .
A. 150.000,-
B. 180.000,-
C. 195.000,-
D. 225.000,-
E. 300.000,-
Pembahasan:
$A+B+C+D=900.000$
$B+C+D=900.000-A$
$A+C+D=900.000-B$
$A+B+D=900.000-C$
$A=\frac{1}{2}(B+C+D)$
$2A=900.000-A$
$3A=900.000\Leftrightarrow A=300.000$
$B=\frac{1}{3}(A+C+D)$
$3B=900.000-B$
$4B=900.000\Leftrightarrow B=225.000$
$C=\frac{1}{4}(A+B+D)$
$4C=900.000-C$
$5C=900.000\Leftrightarrow C=180.000$
$D=900.000-(A+B+C)$
$D=900.000-(300.000+225.000+180.000)$
$D=195.000$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 10
Jika ${{f}^{-1}}(3x-2)=6x+1$ maka $f(x)$ = …
A. $2x+5$
B. $\frac{x+4}{2}$
C. $\frac{x-1}{6}$
D. $\frac{x-2}{5}$
E. $\frac{x-5}{2}$
Pembahasan:
${{f}^{-1}}(3x-2)=6x+1$
$f(6x+1)=3x-2$
$f(6x+1)=\frac{1}{2}(6x+1)-\frac{5}{2}$
$f(x)=\frac{1}{2}x-\frac{5}{2}$
$f(x)=\frac{x-5}{2}$
Jawaban: E
Matematika Dasar SBMPTN 2015 No. 11
Jika $A=\left[ \begin{matrix} 1 & 2 \\ 1 & a \\ \end{matrix} \right]$ matriks yang dapat dibalik, maka hasil kali semua nilai $a$ yang mungkin sehingga $\det (A)=16\det ({{(2A)}^{-1}})$ adalah ..
A. -4 B. -1 C. 0 D. 1 E. 4
Pembahasan:
$\det (A)=16\det ({{(2A)}^{-1}})$
$\det (A)=16.\frac{1}{\det (2A)}$
$\det (A)=\frac{16}{4\det A}$
${{\left( \det (A) \right)}^{2}}=4$
${{(a-2)}^{2}}=4$
${{a}^{2}}-4a=0$
$a(a-4)=0\Rightarrow {{a}_{1}}=0\vee {{a}_{2}}=4$
${{a}_{1}}.{{a}_{2}}=0.4=0$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 12
Jika $a$ dan $b$ adalah bilangan prima dan semua akar ${{x}^{2}}-ax+b=0$ merupakan bilangan bulat positif, maka nilai $a{{b}^{2}}$ adalah …
A. 8 B. 12 C. 18 D. 27 E. 45
Pembahasan:
${{x}^{2}}-ax+b=0$, ${{x}_{1}},{{x}_{2}} > {{B}^{+}}$
${{x}_{1}}.{{x}_{2}}=b$, karena $b$ bilangan prima, maka ${{x}_{1}}=1$
$b={{x}_{2}}$
${{x}_{1}}+{{x}_{2}}=a\Leftrightarrow 1+b=a$
$a-b=1$, $a$ dan $b$ adalah bilangan prima yang selisihnya 1, maka diperoleh $a=3$ dan $b=2$.
Nilai $a{{b}^{2}}={{3.2}^{2}}=12$
Jawaban: B
Matematika Dasar SBMPTN 2015 No. 13
Jika garis $x-2y=3$ tidak memotong maupun menyinggung kurva $y={{x}^{2}}+ax-\frac{15}{16}$, maka …
A. $a > 2$
B. $1 < a < 2$
C. $-1 < a < 2$
D. $-2 < a < -1$
E. $-2 < a < 1$
Pembahasan:
$x-2y=3\Leftrightarrow 2y=x-3$
$y={{x}^{2}}+ax-\frac{15}{16}$
$16y=16{{x}^{2}}+16ax-15$
$8.2y=16{{x}^{2}}+16ax-15$
$8(x-3)=16{{x}^{2}}+16ax-15$
$16{{x}^{2}}+(16a-8)x+9=0$
Tidak memotong maupun tidak menyinggung, maka:
$D < 0$
${{B}^{2}}-4AC < 0$
${{(16a-8)}^{2}}-4.16.9 < 0$
${{(8(2a-1))}^{2}}-4.16.9 < 0$
$64{{(2a-1)}^{2}}-64.9 < 0$
${{(2a-1)}^{2}}-9 < 0$
$4{{a}^{2}}-4a+1-9 < 0$
$4{{a}^{2}}-4a-8 < 0$
${{a}^{2}}-a-2 < 0$
$(a-2)(a+1) < 0$
$-1 < a < 2$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 14
Nilai semua tes matematika dinyatakan dengan bilangan bulat dari 0 sampai dengan 10. Median terkecil yang mungkin bagi siswa yang memiliki rata-rata nilai 6 dari enam kali tes adalah …
A. 3 B. 4 C. 5 D. 6 E. 7
Pembahasan:
Misal nilai yang diperoleh adalah:
${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}},{{x}_{5}},{{x}_{6}}$
$\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}}{6}=6$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}=36$
Agar diperoleh nilai nilai median minimum: $Me=\frac{{{x}_{3}}+{{x}_{4}}}{2}$ maka ${{x}_{5}},{{x}_{6}}$ harus maksimum, diperoleh ${{x}_{5}}=10$ dan ${{x}_{6}}=10$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+10+10=36$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}=16$, ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$ harus minimum
Maka ${{x}_{1}}=4,{{x}_{2}}=4,{{x}_{3}}=4,{{x}_{4}}=4$
$Me=\frac{{{x}_{3}}+{{x}_{4}}}{2}=\frac{4+4}{2}=4$
Jawaban: B
Matematika Dasar SBMPTN 2015 No. 15
Empat buku berjudul Matematika, satu buku berjudul Ekonomi, dan satu buku berjudul Bahasa akan disusun di lemari buku dalam satu baris. Misalkan A adalah kejadian susunan buku sehingga terdapat tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Jika buku dengan judul yang sama tidak dibedakan, maka peluang kejadian A adalah …
A. $\frac{1}{6}$ B. $\frac{1}{5}$ C. $\frac{2}{5}$ D. $\frac{1}{2}$ E. $\frac{3}{5}$
Pembahasan:
4M 1E 1B
MMMMEB maka diperoleh banyak susunannya adalah permutasi 6 unsur dan terdapat 4 unsur sama, maka: $n(S)=\frac{6!}{4!}=\frac{6.5.4!}{4!}=30$.
A = kejadian susunan buku sehingga terdapat 3 atau lebih buku dengan judul yang sama tersusun secara berurutan.
Terdapat 4 buku dengan judul Matematika, anggap 3 buku matematika menjadi satu unsur yaitu ${{M}_{1}}$ dan satu buku matematika yang lain kita sebut ${{M}_{2}}$, sehingga kejadian A adalah menyusun buku-buku dengan judul sebagai berikut:
${{M}_{1}}$ ${{M}_{2}}$ E B (${{M}_{1}}$ dan ${{M}_{2}}$ adalah unsur yang sama).
$n(A)=\frac{4!}{2!}=\frac{4.3.2!}{2!}=12$
$P(A)=\frac{n(A)}{n(S)}=\frac{12}{30}=\frac{2}{5}$
Jawaban: C
#Selamat belajar...! Semoga kalian lulus dan menjadi salah satu mahasiswa di PTN (Perguruan Tinggi Negeri).
Matematika Dasar SBMPTN 2015 No. 1
Diketahui $a$ dan $b$ adalah bilangan real positif. Jika $\frac{(a-\sqrt{b})\sqrt{b}+(a-\sqrt{b})a}{{{a}^{2}}-b}=c$, maka nilai $c$ adalah …
A. $a-\sqrt{b}$
B. ${{a}^{2}}-b$
C. 0
D. 1
E. 2
Pembahasan:
$\frac{(a-\sqrt{b})\sqrt{b}+(a-\sqrt{b})a}{{{a}^{2}}-b}=c$
$\frac{(a-\sqrt{b})(\sqrt{b}+a)}{(a-\sqrt{b})(a+\sqrt{b})}=c$
$1=c$
Jawaban: D
Matematika Dasar SBMPTN 2015 No. 2
Diketahui suatu barisan aritmetika dengan suku pertama dan suku ketiga berturut-turut adalah $k-1$ dan $3k+1$. Jika suku kesepuluh adalah 98, maka suku kelima barisan tersebut adalah …
A. 58 B. 56 C. 48 D. 46 E. 36
Pembahasan:
Barisan Aritmetika: ${{U}_{n}}=a+(n-1)b$
$a=k-1$
${{U}_{3}}=3k+1$
$a+2b=3k+1$
$k-1+2b=3k+1$
$2b=2k+2\Rightarrow b=k+1$
${{U}_{10}}=98$
$a+9b=98$
$k-1+9(k+1)=98$
$10k=90\Leftrightarrow k=9$
$a=k-1\Leftrightarrow a=9-1=8$
$b=k+1\Leftrightarrow b=9+1=10$
${{U}_{5}}=a+4b=8+4.10=48$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 3
Diketahui persegi panjang ABCD. Jika panjang BE = panjang EF = panjang FC = 5 cm dan panjang DG = panjang GH = panjang HC = 3 cm, maka luas daerah yang diarsir adalah … $c{{m}^{2}}$.

A. 22,5
B. 45
C. 60
D. 67,5
E. 90
Pembahasan:
AB = DG + GH + HC = 9 cm
AD = BE + EF + FC = 15 cm
Luas segitiga AEF:
$=\frac{EF\times AB}{2}=\frac{5\times 9}{2}=\frac{45}{2}$
Luas segitiga AGH:
$=\frac{GH\times AD}{2}=\frac{3\times 15}{2}=\frac{45}{2}$
Luas arsiran $=\frac{45}{2}+\frac{45}{2}=45$
Jawaban: B
Matematika Dasar SBMPTN 2015 No. 4
Jika $^{a}\log 2=x$ dan $^{a}\log 5=y$, maka $\log {{a}^{3x}}+3\log {{a}^{y}}$ = …
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
$^{a}\log 2=x\Leftrightarrow {{a}^{x}}=2$
$^{a}\log 5=y\Leftrightarrow {{a}^{y}}=5$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{\left( {{a}^{x}} \right)}^{3}}+\log {{\left( {{a}^{y}} \right)}^{3}}$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{2}^{3}}+\log {{5}^{3}}$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{(2.5)}^{3}}$
$\log {{a}^{3x}}+3\log {{a}^{y}}=\log {{10}^{3}}=3$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 5
Diagram berikut ini menyajikan data (dalam bilangan bulat) nilai sementara dan nilai ujian ulang mahasiswa peserta kuliah Matematika.

Ujian ulang diikuti hanya oleh peserta kuliah tersebut dengan nilai sementara lebih kecil daripada 6. Jika yang dinyatakan lulus adalah mahasiswa yang memperoleh nilai sementara tidak lebih kecil daripada 6 atau nilai ujian ulangnya adalah 6, maka rata-rata nilai mahasiswa yang lulus mata kuliah tersebut adalah …
A. 6,33
B. 6,50
C. 6,75
D. 7,00
E. 7,25
Pembahasan:
Syarat lulus: nilai sementara tidak lebih kecil daripada 6 atau nilai ujian ulangnya 6
Yang lulus berdasarkan nilai sementara:
Nilai 6 ada 1 orang.
Nilai 7 ada 4 orang.
Nilai 8 ada 3 orang.
Yang lulus berdasarkan nilai ujian ulang.
Nilai 6 ada 2 orang.
$\bar{x}=\frac{6.1+7.4+8.3+6.2}{1+4+3+2}=7,00$
Jawaban: D
Matematika Dasar SBMPTN 2015 No. 6
Himpunan penyelesaian pertidaksamaan $\frac{x-1}{x} < 2$ adalah …
A. {$x\in R|x > 0$}
B. {$x\in R|x > -1$}
C. {$x\in R|x < -1$}
D. {$x\in R|x < -1$ atau $x > 0$}
E. {$x\in R|x < 0$ atau $x > 1$}
Pembahasan:
$\frac{x-1}{x} < 2$
$\frac{x-1}{x}-2 < 0 $
$\frac{x-1}{x}-\frac{2x}{x} < 0$
$\frac{-x-1}{x} < 0$
$(-x-1)x < 0$
$(x+1)x > 0$
$x < -1$ atau $x > 0$
Jawaban: D
Matematika Dasar SBMPTN 2015 No. 7
Diketahui suatu fungsi $f$ bersifat $f(-x)=-f(x)$ untuk setiap bilangan real $x$. Jika $f(3)=-5$ dan $f(-5)=1$, maka $f(f(-3))$ = …
A. -5 B. -2 C. -1 D. 1 E. 2
Pembahasan:
$f(f(-3))=f(-f(3))$
$f(f(-3))=f(-(-5))$
$f(f(-3))=f(5)$
$f(-x)=-f(x)\Leftrightarrow f(x)=-f(-x)$
$f(5)=-f(-5)$
$f(5)=-1$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 8
Diketahui sistem persamaan linear
$\frac{2x+1}{3}-\frac{2-3y}{2}=3$
$\frac{4x+y}{6}+\frac{x+y}{3}=2$
Nilai $x+y$ adalah …
A. -3 B. -2 C. 1 D. 2 E. 3
Pembahasan:
$\frac{2x+1}{3}-\frac{2-3y}{2}=3$ kedua ruas kali 6,
$2(2x+1)-3(2-3y)=18$
$4x+9y=22$ …. Persamaan 1
$\frac{4x+y}{6}+\frac{x+y}{3}=2$ kedua ruas kali 6,
$4x+y+2(x+y)=12$
$6x+3y=12$, kalikan dengan 3
$18x+9y=36$ … persamaan 2
$4x+9y=22$ …. Persamaan 1
------------------------------------- (-)
$14x=14\Leftrightarrow x=1$
$4.1+9y=22\Leftrightarrow y=2$
$x+y=1+2=3$
Jawaban: E
Matematika Dasar SBMPTN 2015 No. 9
Empat orang siswa akan mengikuti suatu perlombaan karya inovatif. Untuk itu, diperlukan biaya Rp 900.000,-. Karena masing-masing memiliki kondisi keuangan yang berbeda, besar kontribusi masing-masing siswa tidak sama. Siswa A memberikan kontribusi setengah dari jumlah kontribusi tiga siswa lainnya. Siswa B memberikan kontribusi sepertiga dari jumlah kontribusi tiga siswa lainnya. Siswa C memberikan kontribusi seperempat dari jumlah kontribusi tiga siswa lainnya. Besar kontribusi siswa D adalah Rp . . .
A. 150.000,-
B. 180.000,-
C. 195.000,-
D. 225.000,-
E. 300.000,-
Pembahasan:
$A+B+C+D=900.000$
$B+C+D=900.000-A$
$A+C+D=900.000-B$
$A+B+D=900.000-C$
$A=\frac{1}{2}(B+C+D)$
$2A=900.000-A$
$3A=900.000\Leftrightarrow A=300.000$
$B=\frac{1}{3}(A+C+D)$
$3B=900.000-B$
$4B=900.000\Leftrightarrow B=225.000$
$C=\frac{1}{4}(A+B+D)$
$4C=900.000-C$
$5C=900.000\Leftrightarrow C=180.000$
$D=900.000-(A+B+C)$
$D=900.000-(300.000+225.000+180.000)$
$D=195.000$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 10
Jika ${{f}^{-1}}(3x-2)=6x+1$ maka $f(x)$ = …
A. $2x+5$
B. $\frac{x+4}{2}$
C. $\frac{x-1}{6}$
D. $\frac{x-2}{5}$
E. $\frac{x-5}{2}$
Pembahasan:
${{f}^{-1}}(3x-2)=6x+1$
$f(6x+1)=3x-2$
$f(6x+1)=\frac{1}{2}(6x+1)-\frac{5}{2}$
$f(x)=\frac{1}{2}x-\frac{5}{2}$
$f(x)=\frac{x-5}{2}$
Jawaban: E
Matematika Dasar SBMPTN 2015 No. 11
Jika $A=\left[ \begin{matrix} 1 & 2 \\ 1 & a \\ \end{matrix} \right]$ matriks yang dapat dibalik, maka hasil kali semua nilai $a$ yang mungkin sehingga $\det (A)=16\det ({{(2A)}^{-1}})$ adalah ..
A. -4 B. -1 C. 0 D. 1 E. 4
Pembahasan:
$\det (A)=16\det ({{(2A)}^{-1}})$
$\det (A)=16.\frac{1}{\det (2A)}$
$\det (A)=\frac{16}{4\det A}$
${{\left( \det (A) \right)}^{2}}=4$
${{(a-2)}^{2}}=4$
${{a}^{2}}-4a=0$
$a(a-4)=0\Rightarrow {{a}_{1}}=0\vee {{a}_{2}}=4$
${{a}_{1}}.{{a}_{2}}=0.4=0$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 12
Jika $a$ dan $b$ adalah bilangan prima dan semua akar ${{x}^{2}}-ax+b=0$ merupakan bilangan bulat positif, maka nilai $a{{b}^{2}}$ adalah …
A. 8 B. 12 C. 18 D. 27 E. 45
Pembahasan:
${{x}^{2}}-ax+b=0$, ${{x}_{1}},{{x}_{2}} > {{B}^{+}}$
${{x}_{1}}.{{x}_{2}}=b$, karena $b$ bilangan prima, maka ${{x}_{1}}=1$
$b={{x}_{2}}$
${{x}_{1}}+{{x}_{2}}=a\Leftrightarrow 1+b=a$
$a-b=1$, $a$ dan $b$ adalah bilangan prima yang selisihnya 1, maka diperoleh $a=3$ dan $b=2$.
Nilai $a{{b}^{2}}={{3.2}^{2}}=12$
Jawaban: B
Matematika Dasar SBMPTN 2015 No. 13
Jika garis $x-2y=3$ tidak memotong maupun menyinggung kurva $y={{x}^{2}}+ax-\frac{15}{16}$, maka …
A. $a > 2$
B. $1 < a < 2$
C. $-1 < a < 2$
D. $-2 < a < -1$
E. $-2 < a < 1$
Pembahasan:
$x-2y=3\Leftrightarrow 2y=x-3$
$y={{x}^{2}}+ax-\frac{15}{16}$
$16y=16{{x}^{2}}+16ax-15$
$8.2y=16{{x}^{2}}+16ax-15$
$8(x-3)=16{{x}^{2}}+16ax-15$
$16{{x}^{2}}+(16a-8)x+9=0$
Tidak memotong maupun tidak menyinggung, maka:
$D < 0$
${{B}^{2}}-4AC < 0$
${{(16a-8)}^{2}}-4.16.9 < 0$
${{(8(2a-1))}^{2}}-4.16.9 < 0$
$64{{(2a-1)}^{2}}-64.9 < 0$
${{(2a-1)}^{2}}-9 < 0$
$4{{a}^{2}}-4a+1-9 < 0$
$4{{a}^{2}}-4a-8 < 0$
${{a}^{2}}-a-2 < 0$
$(a-2)(a+1) < 0$
$-1 < a < 2$
Jawaban: C
Matematika Dasar SBMPTN 2015 No. 14
Nilai semua tes matematika dinyatakan dengan bilangan bulat dari 0 sampai dengan 10. Median terkecil yang mungkin bagi siswa yang memiliki rata-rata nilai 6 dari enam kali tes adalah …
A. 3 B. 4 C. 5 D. 6 E. 7
Pembahasan:
Misal nilai yang diperoleh adalah:
${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}},{{x}_{5}},{{x}_{6}}$
$\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}}{6}=6$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}=36$
Agar diperoleh nilai nilai median minimum: $Me=\frac{{{x}_{3}}+{{x}_{4}}}{2}$ maka ${{x}_{5}},{{x}_{6}}$ harus maksimum, diperoleh ${{x}_{5}}=10$ dan ${{x}_{6}}=10$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+10+10=36$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}=16$, ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$ harus minimum
Maka ${{x}_{1}}=4,{{x}_{2}}=4,{{x}_{3}}=4,{{x}_{4}}=4$
$Me=\frac{{{x}_{3}}+{{x}_{4}}}{2}=\frac{4+4}{2}=4$
Jawaban: B
Matematika Dasar SBMPTN 2015 No. 15
Empat buku berjudul Matematika, satu buku berjudul Ekonomi, dan satu buku berjudul Bahasa akan disusun di lemari buku dalam satu baris. Misalkan A adalah kejadian susunan buku sehingga terdapat tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Jika buku dengan judul yang sama tidak dibedakan, maka peluang kejadian A adalah …
A. $\frac{1}{6}$ B. $\frac{1}{5}$ C. $\frac{2}{5}$ D. $\frac{1}{2}$ E. $\frac{3}{5}$
Pembahasan:
4M 1E 1B
MMMMEB maka diperoleh banyak susunannya adalah permutasi 6 unsur dan terdapat 4 unsur sama, maka: $n(S)=\frac{6!}{4!}=\frac{6.5.4!}{4!}=30$.
A = kejadian susunan buku sehingga terdapat 3 atau lebih buku dengan judul yang sama tersusun secara berurutan.
Terdapat 4 buku dengan judul Matematika, anggap 3 buku matematika menjadi satu unsur yaitu ${{M}_{1}}$ dan satu buku matematika yang lain kita sebut ${{M}_{2}}$, sehingga kejadian A adalah menyusun buku-buku dengan judul sebagai berikut:
${{M}_{1}}$ ${{M}_{2}}$ E B (${{M}_{1}}$ dan ${{M}_{2}}$ adalah unsur yang sama).
$n(A)=\frac{4!}{2!}=\frac{4.3.2!}{2!}=12$
$P(A)=\frac{n(A)}{n(S)}=\frac{12}{30}=\frac{2}{5}$
Jawaban: C
Artikel Terkait:
|

Post a Comment for "Pembahasan SBMPTN 2015 Matematika Dasar"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.