Pembahasan SBMPTN 2013 Matematika Dasar Kode 125
Berbagi itu indah, dengan berbagi kita tidak akan kehilangan apapun, malah menambah, yaitu menambah sukacita, menambah teman. Jadi, kalau teman-teman pembaca catatan matematika ingin share postingan ini, dipersilahkan dengan senang hati. Nah, jika teman-teman ingin belajar secara mandiri lebih dahulu, saya sarankan silahkan download soalnya disini.
Matematika Dasar SBMPTN 2013 No. 1
Jika ${{9}^{m-1}}+{{9}^{m+1}}=82$, maka ${{4}^{m+1}}$ = …
A. $\frac{1}{16}$ B. $\frac{1}{4}$ C. 4 D. 16 E. 64
Pembahasan:
${{9}^{m-1}}+{{9}^{m+1}}=82$
$\frac{{{9}^{m}}}{9}+{{9.9}^{m}}=82$
${{9}^{m}}+{{81.9}^{m}}=82.9$
${{82.9}^{m}}=82.9$
${{9}^{m}}=9\Rightarrow m=1$
${{4}^{m+1}}={{4}^{1+1}}=16$
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 2
Jika ${}^{3}\log a-2({}^{3}\log b)=1$ dan ${}^{3}\log b-2({}^{3}\log a)=-2$, maka nilai $ab$ adalah …
A. 2 B. 3 C. 6 D. 9 E. 12
Pembahasan:
${}^{3}\log a-2({}^{3}\log b)=1$
$2.{}^{3}\log a-4({}^{3}\log b)=2$
${}^{3}\log b-2({}^{3}\log a)=-2$
--------------------------------- (+)
$-3.{}^{3}\log b=0$
${}^{3}\log b=0\Rightarrow b=1$
Substitusi ke:
${}^{3}\log a-2({}^{3}\log b)=1$
${}^{3}\log a-2({}^{3}\log 1)=1$
${}^{3}\log a=1\Rightarrow a=3$
$ab=3.1=3$
Jawaban: B
Matematika Dasar SBMPTN 2013 No. 3
Persamaan kuadrat ${{x}^{2}}-(p+2)x-p=0$ mempunyai akar-akar ${{x}_{1}}$ dan ${{x}_{2}}$. Jika ${{x}_{2}}({{x}_{1}}+1)=-2$, maka nilai $p$ adalah …
A. $-\frac{8}{5}$ B. $-\frac{5}{6}$ C. $\frac{5}{8}$ D. $\frac{8}{5}$ E. 2
Pembahasan:
${{x}^{2}}-(p+2)x-p=0$
${{x}_{1}}+{{x}_{2}}=p+2$
${{x}_{1}}.{{x}_{2}}=-p$
${{x}_{2}}({{x}_{1}}+1)=-2$
${{x}_{1}}.{{x}_{2}}+{{x}_{2}}=-2$
$-p+{{x}_{2}}=-2\Rightarrow {{x}_{2}}=p-2$
${{x}_{1}}+{{x}_{2}}=p+2$
${{x}_{1}}+p-2=p+2\Leftrightarrow {{x}_{1}}=4$
Substitusi ke:
${{x}^{2}}-(p+2)x-p=0$
${{4}^{2}}-(p+2).4-p=0$
$16-4p-8-p=0$
$-5p=-8\Leftrightarrow p=\frac{8}{5}$
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 4
Jika grafik fungsi kuadrat $f(x)=a{{x}^{2}}+bx+c$ mempunyai titik puncak $(8,4)$ dan memotong sumbu-x negatif, maka …
A. a > 0, b > 0, dan c > 0
B. a < 0, b < 0, dan c > 0
C. a < 0, b > 0, dan c < 0
D. a > 0, b > 0, dan c < 0
E. a < 0, b > 0, dan c > 0
Pembahasan:
Perhatikan sketsa gambar berikut!
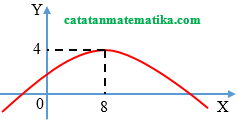
Parabola terbuka ke atas maka a < 0.
Puncak di kanan sumbu Y maka ab < 0, maka b > 0
Parabola memotong sumbu Y positif maka c > 0
Jawaban: E
Matematika dasar SBMPTN 2013 No. 5
Ibu mendapat potongan harga sebesar 25% dari total pembelian barang di suatu toko. Toko tersebut membebankan pajak sebesar 10% dari harga total pembelian setelah dipotong. Jika $x$ adalah harga total pembelian, maka ibu harus membayar sebesar …
A. $(0,1\times 0,25)x$
B. $(0,9\times 0,25)x$
C. $(0,9\times 0,75)x$
D. $(1,1\times 0,25)x$
E. $(1,1\times 0,75)x$
Pembahasan:
Misalkan harga pembelian = x
Diskon = 25%
Pajak = 10%
Total pembayaran = (100% - diskon)(1 + %pajak)(harga pembelian)
= (100% - 25%)(1 + 10%).x
= (0,75)(1,1)x
Jawaban: E
Matematika Dasar SBMPTN 2013 No. 6
Jika $-2 < a < 1$ maka semua nilai $x$ yang memenuhi pertidaksamaan $\frac{{{x}^{2}}-3x-3a}{(2-x)(x+3)} \le 0$ adalah …
A. $x < -2$ atau $x > 3$
B. $x < -3$ atau $x > 2$
C. $-3 < x < -2$
D. $-3 < x < 2$
E. $-2 < x < 3$
Pembahasan:
Perhatikan pembilang
${{x}^{2}}-3x-3a$
$D={{b}^{2}}-4ac$
$D=9+12a < 0$ untuk $-2 < a < 1$
Dapat disimpulkan bahwa ${{x}^{2}}-3x-3a > 0$, akibatnya:
$(2-x)(x+3) < 0$
$(x-2)(x+3) > 0$
$x < -3$ atau $x > 2$
Jawaban: B
Matematika Dasar SBMPTN 2013 No. 7
Anang bekerja di toko obat pada pagi hari dan di rumah makan pada malam hari. Setiap bulan ia memperoleh gaji dari toko obat sebesar Rp. 1.000.000,00 dan bonus 10% dari penjualan, sedangkan dari rumah makan ia memperoleh sebesar Rp. 600.000,00 dan bonus 25% dari penjualan. Jika pada bulan lalu pendapatan Anang dari rumah makan dua kali pendapatannya dari toko obat, maka pendapatan Anang dari toko obat pada bulan tersebut adalah …
A. Rp. 3.900.000,00
B. Rp. 3.800.000,00
C. Rp. 3.700.000,00
D. Rp. 3.600.000,00
E. Rp. 3.500.000,00
Pembahasan:
Misalkan penjualan sama yaitu x.
$600.000+\frac{25}{100}x=2(1.000.000+\frac{10}{100}x)$
$600.000+\frac{25}{100}x=2.000.000+\frac{20}{100}x$
$\frac{5}{100}x=1.400.000$
$x=28.000.000$
Jadi, pendapatan dari toko obat
$=1.000.000+\frac{10}{100}(28.000.000)$
$=3.800.000$
Jawaban: B
Matematika Dasar SBMPTN 2013 No. 8
Distribusi berat bayi di rumah sakit A dan B dapat dilihat pada diagram berikut!
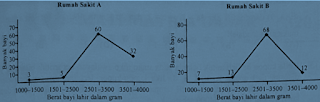
Berat badan bayi dikatakan normal apabila berat lahirnya lebih dari 2500 gram. Banyak bayi normal yang lahir di dua rumah sakit tersebut adalah …
A. 12 B. 32 C. 44 D. 128 E. 172
Pembahasan:
Banyak bayi normal yang lahir dari rumah sakit A = 60 + 32 = 92
Banyak bayi normal yang lahir dari rumah sakit B = 68 + 12 = 80
Total bayi normal yang lahir = 92 + 80 = 172
Jawaban: E
Matematika Dasar SBMPTN 2013 No. 9
Median dan rata-rata dari data yang terdiri dari empat bilangan asli yang telah diurutkan mulai dari yang terkecil adalah 8. Jika selisih antara data terbesar dan terkecilnya adalah 10 dan modusnya tunggal, maka hasil kali data kedua dan keempatnya adalah ..
A. 65 B. 78 C. 91 D. 104 E. 117
Pembahasan:
Misalkan data diurutkan sebagai berikut:
a, b, c, d
$Me=\frac{b+c}{2}=8\Leftrightarrow b+c=16$
$\bar{x}=\frac{a+b+c+d}{4}=8$
$a+b+c+d=32$
$a+16+d=32\Leftrightarrow d+a=16$ … (1)
Jangkauan = 10, maka:
$d-a=10$
$d+a=16$
-------------- (+)
$2d=26\Leftrightarrow d=13$, $a=3$,
Karena modusnya tunggal, maka b = 8 dan c = 8
Jadi, b.d = 8.13 = 104
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 10
Jika $f\left( \frac{1}{x+1} \right)=\frac{x+3}{x+1}$, maka nilai $(a-3)$ agar ${{f}^{-1}}(a+1)=2$ adalah …
A. $-\frac{3}{2}$ B. $-\frac{1}{2}$ C. 0 D. 1 E. 2
Pembahasan:
${{f}^{-1}}(a+1)=2$
$f(2)=a+1$
$f\left( \frac{1}{x+1} \right)=\frac{x+3}{x+1}$
Maka:
$2=\frac{1}{x+1}$
$2x+2=1\Leftrightarrow x=-\frac{1}{2}$
$a+1=\frac{x+3}{x+1}$
$a+1=\frac{-\frac{1}{2}+3}{-\frac{1}{2}+1}$
$a+1=5\Leftrightarrow a=4$
$a-3=4-3=1$
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 11
Jika $A=\left( \begin{matrix} a & 1 & a \\ -1 & a & 2 \\ \end{matrix} \right)$ , $B=\left( \begin{matrix} -2 & 1 \\ 1 & 0 \\ 1 & -1 \\ \end{matrix} \right)$, dan determinan AB adalah 6, maka nilai ${{a}^{2}}-3a$ adalah …
A. -2 B. -1 C. 0 D. 1 E. 2
Pembahasan:
$AB=\left( \begin{matrix} a & 1 & a \\ -1 & a & 2 \\ \end{matrix} \right).\left( \begin{matrix} -2 & 1 \\ 1 & 0 \\ 1 & -1 \\ \end{matrix} \right)$
$AB=\left( \begin{matrix} -2a+1+a & a+0-a \\ 2+a+2 & -1+0-2 \\ \end{matrix} \right)$
$AB=\left( \begin{matrix} -a+1 & 0 \\ a+4 & -3 \\ \end{matrix} \right)$
$\det (AB)=3a-3-0=6$
$3a=9\Leftrightarrow a=3$
${{a}^{2}}-3a={{3}^{2}}-3.3=0$
Jawaban: C
Matematika Dasar SBMPTN 2013 No. 12
Diketahui, a, b, dan c berturut-turut suku ke-2, ke-4 dan ke-6 suatu barisan aritmetika. Jika $\frac{a+b+c}{b-1}=4$, maka nilai b adalah …
A. 4 B. 2 C. -1 D. -2 E. -4
Pembahasan:
Barisan aritmetika:
${{U}_{2}}=a$, ${{U}_{4}}=b$, ${{U}_{6}}=c$
$2{{U}_{4}}={{U}_{2}}+{{U}_{6}}$
$2b=a+c$
$\frac{a+b+c}{b-1}=4$
$\frac{b+a+c}{b-1}=4$
$\frac{b+2b}{b-1}=4$
$3b=4b-4$
$-b=-4\Leftrightarrow b=4$
Jawaban: A
Matematika Dasar SBMPTN 2013 No. 13
Diketahui deret geometri tak hingga ${{u}_{1}}+{{u}_{2}}+{{u}_{3}}+...$ . Jika rasio deret tersebut adalah r dengan $-1 < r < 1$, ${{u}_{1}}+{{u}_{3}}+{{u}_{5}}+...=8$, dan ${{u}_{1}}+{{u}_{3}}=\frac{15}{2}$, maka nilai ${{r}^{2}}$ adalah …
A. $\frac{1}{8}$ B. $\frac{1}{6}$ C. $\frac{1}{4}$ D. $\frac{1}{3}$ E. $\frac{1}{2}$
Pembahasan:
Deret geometri tak hingga
${{u}_{1}}+{{u}_{3}}+{{u}_{5}}+...=8$
$\frac{a}{1-{{r}^{2}}}=8\Leftrightarrow a=8-8{{r}^{2}}$
${{u}_{1}}+{{u}_{3}}=\frac{15}{2}$
$a+a{{r}^{2}}=\frac{15}{2}$
$a(1+{{r}^{2}})=\frac{15}{2}$
$(8-8{{r}^{2}})(1+{{r}^{2}})=\frac{15}{2}$
$8+8{{r}^{2}}-8{{r}^{2}}-8{{r}^{4}}=\frac{15}{2}$
$-8{{r}^{4}}=\frac{15}{2}-8$
$-8{{r}^{4}}=\frac{-1}{2}$
${{r}^{4}}=\frac{1}{16}\Leftrightarrow {{r}^{2}}=\frac{1}{4}$
Jawaban: C
Matematika Dasar SBMPTN 2013 No. 14
Parabola $y={{x}^{2}}-(2k-3)x+k$ memotong sumbu Y di $(0,c)$ dan memotong sumbu X di $(a,0)$ dan $(b,0)$. Jika $3a-2$, $\frac{3}{2}c-2$, dan $2b-a$ membentuk barisan aritmetika, maka nilai k adalah …
A. 4 B. 2 C. 1 D. -2 E. -4
Pembahasan:
$y={{x}^{2}}-(2k-3)x+k$ memotong sumbu Y, x = 0
$y=k\Leftrightarrow c=k$
$y={{x}^{2}}-(2k-3)x+k$ memotong sumbu X di $(a,0)$ dan $(b,0)$, maka:
$a+b=2k-3$
Barisan aritmetika:
$3a-2$, $\frac{3}{2}c-2$, dan $2b-a$
$2(\frac{3}{2}c-2)=3a-2+2b-a$
$3c-4=2a+2b-2$
$3c-4=2(a+b)-2$
$3k-4=2(2k-3)-2$
$3k-4=4k-6-2$
$4=k$
Jawaban: A
Matematika Dasar SBMPTN 2013 No. 15
Kode kupon hadiah untuk belanja pada suatu toko swalayan berbentuk bilangan yang disusun dari angka 2, 4, 4, 6, 8. Jika kupon-kupon tersebut disusun berdasarkan kodenya dari mulai yang terkecil sampai dengan yang terbesar, maka kupon dengan kode kurang daripada 64000 sebanyak …
A. 40 B. 39 C. 36 D. 32 E. 24
Pembahasan:
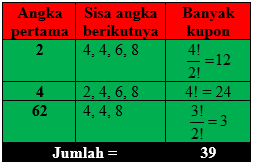
Jawaban: B
Matematika Dasar SBMPTN 2013 No. 1
Jika ${{9}^{m-1}}+{{9}^{m+1}}=82$, maka ${{4}^{m+1}}$ = …
A. $\frac{1}{16}$ B. $\frac{1}{4}$ C. 4 D. 16 E. 64
Pembahasan:
${{9}^{m-1}}+{{9}^{m+1}}=82$
$\frac{{{9}^{m}}}{9}+{{9.9}^{m}}=82$
${{9}^{m}}+{{81.9}^{m}}=82.9$
${{82.9}^{m}}=82.9$
${{9}^{m}}=9\Rightarrow m=1$
${{4}^{m+1}}={{4}^{1+1}}=16$
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 2
Jika ${}^{3}\log a-2({}^{3}\log b)=1$ dan ${}^{3}\log b-2({}^{3}\log a)=-2$, maka nilai $ab$ adalah …
A. 2 B. 3 C. 6 D. 9 E. 12
Pembahasan:
${}^{3}\log a-2({}^{3}\log b)=1$
$2.{}^{3}\log a-4({}^{3}\log b)=2$
${}^{3}\log b-2({}^{3}\log a)=-2$
--------------------------------- (+)
$-3.{}^{3}\log b=0$
${}^{3}\log b=0\Rightarrow b=1$
Substitusi ke:
${}^{3}\log a-2({}^{3}\log b)=1$
${}^{3}\log a-2({}^{3}\log 1)=1$
${}^{3}\log a=1\Rightarrow a=3$
$ab=3.1=3$
Jawaban: B
Matematika Dasar SBMPTN 2013 No. 3
Persamaan kuadrat ${{x}^{2}}-(p+2)x-p=0$ mempunyai akar-akar ${{x}_{1}}$ dan ${{x}_{2}}$. Jika ${{x}_{2}}({{x}_{1}}+1)=-2$, maka nilai $p$ adalah …
A. $-\frac{8}{5}$ B. $-\frac{5}{6}$ C. $\frac{5}{8}$ D. $\frac{8}{5}$ E. 2
Pembahasan:
${{x}^{2}}-(p+2)x-p=0$
${{x}_{1}}+{{x}_{2}}=p+2$
${{x}_{1}}.{{x}_{2}}=-p$
${{x}_{2}}({{x}_{1}}+1)=-2$
${{x}_{1}}.{{x}_{2}}+{{x}_{2}}=-2$
$-p+{{x}_{2}}=-2\Rightarrow {{x}_{2}}=p-2$
${{x}_{1}}+{{x}_{2}}=p+2$
${{x}_{1}}+p-2=p+2\Leftrightarrow {{x}_{1}}=4$
Substitusi ke:
${{x}^{2}}-(p+2)x-p=0$
${{4}^{2}}-(p+2).4-p=0$
$16-4p-8-p=0$
$-5p=-8\Leftrightarrow p=\frac{8}{5}$
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 4
Jika grafik fungsi kuadrat $f(x)=a{{x}^{2}}+bx+c$ mempunyai titik puncak $(8,4)$ dan memotong sumbu-x negatif, maka …
A. a > 0, b > 0, dan c > 0
B. a < 0, b < 0, dan c > 0
C. a < 0, b > 0, dan c < 0
D. a > 0, b > 0, dan c < 0
E. a < 0, b > 0, dan c > 0
Pembahasan:
Perhatikan sketsa gambar berikut!

Parabola terbuka ke atas maka a < 0.
Puncak di kanan sumbu Y maka ab < 0, maka b > 0
Parabola memotong sumbu Y positif maka c > 0
Jawaban: E
Matematika dasar SBMPTN 2013 No. 5
Ibu mendapat potongan harga sebesar 25% dari total pembelian barang di suatu toko. Toko tersebut membebankan pajak sebesar 10% dari harga total pembelian setelah dipotong. Jika $x$ adalah harga total pembelian, maka ibu harus membayar sebesar …
A. $(0,1\times 0,25)x$
B. $(0,9\times 0,25)x$
C. $(0,9\times 0,75)x$
D. $(1,1\times 0,25)x$
E. $(1,1\times 0,75)x$
Pembahasan:
Misalkan harga pembelian = x
Diskon = 25%
Pajak = 10%
Total pembayaran = (100% - diskon)(1 + %pajak)(harga pembelian)
= (100% - 25%)(1 + 10%).x
= (0,75)(1,1)x
Jawaban: E
Matematika Dasar SBMPTN 2013 No. 6
Jika $-2 < a < 1$ maka semua nilai $x$ yang memenuhi pertidaksamaan $\frac{{{x}^{2}}-3x-3a}{(2-x)(x+3)} \le 0$ adalah …
A. $x < -2$ atau $x > 3$
B. $x < -3$ atau $x > 2$
C. $-3 < x < -2$
D. $-3 < x < 2$
E. $-2 < x < 3$
Pembahasan:
Perhatikan pembilang
${{x}^{2}}-3x-3a$
$D={{b}^{2}}-4ac$
$D=9+12a < 0$ untuk $-2 < a < 1$
Dapat disimpulkan bahwa ${{x}^{2}}-3x-3a > 0$, akibatnya:
$(2-x)(x+3) < 0$
$(x-2)(x+3) > 0$
$x < -3$ atau $x > 2$
Jawaban: B
Matematika Dasar SBMPTN 2013 No. 7
Anang bekerja di toko obat pada pagi hari dan di rumah makan pada malam hari. Setiap bulan ia memperoleh gaji dari toko obat sebesar Rp. 1.000.000,00 dan bonus 10% dari penjualan, sedangkan dari rumah makan ia memperoleh sebesar Rp. 600.000,00 dan bonus 25% dari penjualan. Jika pada bulan lalu pendapatan Anang dari rumah makan dua kali pendapatannya dari toko obat, maka pendapatan Anang dari toko obat pada bulan tersebut adalah …
A. Rp. 3.900.000,00
B. Rp. 3.800.000,00
C. Rp. 3.700.000,00
D. Rp. 3.600.000,00
E. Rp. 3.500.000,00
Pembahasan:
Misalkan penjualan sama yaitu x.
$600.000+\frac{25}{100}x=2(1.000.000+\frac{10}{100}x)$
$600.000+\frac{25}{100}x=2.000.000+\frac{20}{100}x$
$\frac{5}{100}x=1.400.000$
$x=28.000.000$
Jadi, pendapatan dari toko obat
$=1.000.000+\frac{10}{100}(28.000.000)$
$=3.800.000$
Jawaban: B
Matematika Dasar SBMPTN 2013 No. 8
Distribusi berat bayi di rumah sakit A dan B dapat dilihat pada diagram berikut!

Berat badan bayi dikatakan normal apabila berat lahirnya lebih dari 2500 gram. Banyak bayi normal yang lahir di dua rumah sakit tersebut adalah …
A. 12 B. 32 C. 44 D. 128 E. 172
Pembahasan:
Banyak bayi normal yang lahir dari rumah sakit A = 60 + 32 = 92
Banyak bayi normal yang lahir dari rumah sakit B = 68 + 12 = 80
Total bayi normal yang lahir = 92 + 80 = 172
Jawaban: E
Matematika Dasar SBMPTN 2013 No. 9
Median dan rata-rata dari data yang terdiri dari empat bilangan asli yang telah diurutkan mulai dari yang terkecil adalah 8. Jika selisih antara data terbesar dan terkecilnya adalah 10 dan modusnya tunggal, maka hasil kali data kedua dan keempatnya adalah ..
A. 65 B. 78 C. 91 D. 104 E. 117
Pembahasan:
Misalkan data diurutkan sebagai berikut:
a, b, c, d
$Me=\frac{b+c}{2}=8\Leftrightarrow b+c=16$
$\bar{x}=\frac{a+b+c+d}{4}=8$
$a+b+c+d=32$
$a+16+d=32\Leftrightarrow d+a=16$ … (1)
Jangkauan = 10, maka:
$d-a=10$
$d+a=16$
-------------- (+)
$2d=26\Leftrightarrow d=13$, $a=3$,
Karena modusnya tunggal, maka b = 8 dan c = 8
Jadi, b.d = 8.13 = 104
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 10
Jika $f\left( \frac{1}{x+1} \right)=\frac{x+3}{x+1}$, maka nilai $(a-3)$ agar ${{f}^{-1}}(a+1)=2$ adalah …
A. $-\frac{3}{2}$ B. $-\frac{1}{2}$ C. 0 D. 1 E. 2
Pembahasan:
${{f}^{-1}}(a+1)=2$
$f(2)=a+1$
$f\left( \frac{1}{x+1} \right)=\frac{x+3}{x+1}$
Maka:
$2=\frac{1}{x+1}$
$2x+2=1\Leftrightarrow x=-\frac{1}{2}$
$a+1=\frac{x+3}{x+1}$
$a+1=\frac{-\frac{1}{2}+3}{-\frac{1}{2}+1}$
$a+1=5\Leftrightarrow a=4$
$a-3=4-3=1$
Jawaban: D
Matematika Dasar SBMPTN 2013 No. 11
Jika $A=\left( \begin{matrix} a & 1 & a \\ -1 & a & 2 \\ \end{matrix} \right)$ , $B=\left( \begin{matrix} -2 & 1 \\ 1 & 0 \\ 1 & -1 \\ \end{matrix} \right)$, dan determinan AB adalah 6, maka nilai ${{a}^{2}}-3a$ adalah …
A. -2 B. -1 C. 0 D. 1 E. 2
Pembahasan:
$AB=\left( \begin{matrix} a & 1 & a \\ -1 & a & 2 \\ \end{matrix} \right).\left( \begin{matrix} -2 & 1 \\ 1 & 0 \\ 1 & -1 \\ \end{matrix} \right)$
$AB=\left( \begin{matrix} -2a+1+a & a+0-a \\ 2+a+2 & -1+0-2 \\ \end{matrix} \right)$
$AB=\left( \begin{matrix} -a+1 & 0 \\ a+4 & -3 \\ \end{matrix} \right)$
$\det (AB)=3a-3-0=6$
$3a=9\Leftrightarrow a=3$
${{a}^{2}}-3a={{3}^{2}}-3.3=0$
Jawaban: C
Matematika Dasar SBMPTN 2013 No. 12
Diketahui, a, b, dan c berturut-turut suku ke-2, ke-4 dan ke-6 suatu barisan aritmetika. Jika $\frac{a+b+c}{b-1}=4$, maka nilai b adalah …
A. 4 B. 2 C. -1 D. -2 E. -4
Pembahasan:
Barisan aritmetika:
${{U}_{2}}=a$, ${{U}_{4}}=b$, ${{U}_{6}}=c$
$2{{U}_{4}}={{U}_{2}}+{{U}_{6}}$
$2b=a+c$
$\frac{a+b+c}{b-1}=4$
$\frac{b+a+c}{b-1}=4$
$\frac{b+2b}{b-1}=4$
$3b=4b-4$
$-b=-4\Leftrightarrow b=4$
Jawaban: A
Matematika Dasar SBMPTN 2013 No. 13
Diketahui deret geometri tak hingga ${{u}_{1}}+{{u}_{2}}+{{u}_{3}}+...$ . Jika rasio deret tersebut adalah r dengan $-1 < r < 1$, ${{u}_{1}}+{{u}_{3}}+{{u}_{5}}+...=8$, dan ${{u}_{1}}+{{u}_{3}}=\frac{15}{2}$, maka nilai ${{r}^{2}}$ adalah …
A. $\frac{1}{8}$ B. $\frac{1}{6}$ C. $\frac{1}{4}$ D. $\frac{1}{3}$ E. $\frac{1}{2}$
Pembahasan:
Deret geometri tak hingga
${{u}_{1}}+{{u}_{3}}+{{u}_{5}}+...=8$
$\frac{a}{1-{{r}^{2}}}=8\Leftrightarrow a=8-8{{r}^{2}}$
${{u}_{1}}+{{u}_{3}}=\frac{15}{2}$
$a+a{{r}^{2}}=\frac{15}{2}$
$a(1+{{r}^{2}})=\frac{15}{2}$
$(8-8{{r}^{2}})(1+{{r}^{2}})=\frac{15}{2}$
$8+8{{r}^{2}}-8{{r}^{2}}-8{{r}^{4}}=\frac{15}{2}$
$-8{{r}^{4}}=\frac{15}{2}-8$
$-8{{r}^{4}}=\frac{-1}{2}$
${{r}^{4}}=\frac{1}{16}\Leftrightarrow {{r}^{2}}=\frac{1}{4}$
Jawaban: C
Matematika Dasar SBMPTN 2013 No. 14
Parabola $y={{x}^{2}}-(2k-3)x+k$ memotong sumbu Y di $(0,c)$ dan memotong sumbu X di $(a,0)$ dan $(b,0)$. Jika $3a-2$, $\frac{3}{2}c-2$, dan $2b-a$ membentuk barisan aritmetika, maka nilai k adalah …
A. 4 B. 2 C. 1 D. -2 E. -4
Pembahasan:
$y={{x}^{2}}-(2k-3)x+k$ memotong sumbu Y, x = 0
$y=k\Leftrightarrow c=k$
$y={{x}^{2}}-(2k-3)x+k$ memotong sumbu X di $(a,0)$ dan $(b,0)$, maka:
$a+b=2k-3$
Barisan aritmetika:
$3a-2$, $\frac{3}{2}c-2$, dan $2b-a$
$2(\frac{3}{2}c-2)=3a-2+2b-a$
$3c-4=2a+2b-2$
$3c-4=2(a+b)-2$
$3k-4=2(2k-3)-2$
$3k-4=4k-6-2$
$4=k$
Jawaban: A
Matematika Dasar SBMPTN 2013 No. 15
Kode kupon hadiah untuk belanja pada suatu toko swalayan berbentuk bilangan yang disusun dari angka 2, 4, 4, 6, 8. Jika kupon-kupon tersebut disusun berdasarkan kodenya dari mulai yang terkecil sampai dengan yang terbesar, maka kupon dengan kode kurang daripada 64000 sebanyak …
A. 40 B. 39 C. 36 D. 32 E. 24
Pembahasan:

Jawaban: B
Artikel Terkait:
|

Post a Comment for "Pembahasan SBMPTN 2013 Matematika Dasar Kode 125"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.