Pembahasan SBMPTN 2014 Matematika Dasar Kode 614
Berikut ini adalah Soal dan Pembahasan Matematika Dasar SBMPTN Tahun 2014 dengan kode soal 614. Mungkin soal ini bagi beberapa orang sudah expire, tapi bagi yang ingin belajar saya yakin bahwa tidak ada istilah expire, dan saya berharap soal dan pembahasan ini bermanfaat bagi teman-teman pengunjung setiap "Catatan Matematika", dan kiranya soal ini dapat dijadikan sebagai bahan belajar. Seperti biasa, cobalah belajar itu dimulai secara mandiri dengan cara download soal tanpa pembahasan, setelah itu silahkan didiskusikan atau dipelajari pembahasan berikut ini.
Matematika Dasar SBMPTN 2014 No. 1
Jika $\left( \begin{matrix} y \\ x \\ \end{matrix} \right)={{\left( \begin{matrix} 2 & 1 \\ -1 & x \\ \end{matrix} \right)}^{-1}}\left( \begin{matrix} 4 \\ -1 \\ \end{matrix} \right)$ dengan $x\ne -\frac{1}{2}$, maka nilai $\frac{1}{2}x+y$ = …
A. -4 B. -2 C. 0 D. 2 E. 4
Pembahasan:
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)={{\left( \begin{matrix} 2 & 1 \\ -1 & x \\ \end{matrix} \right)}^{-1}}\left( \begin{matrix} 4 \\ -1 \\ \end{matrix} \right)$
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)=\frac{1}{2x+1}\left( \begin{matrix} x & -1 \\ 1 & 2 \\ \end{matrix} \right)\left( \begin{matrix} 4 \\ -1 \\ \end{matrix} \right)$
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)=\frac{1}{2x+1}\left( \begin{matrix} 4x+1 \\ 4-2 \\ \end{matrix} \right)$
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)=\left( \begin{matrix} \frac{4x+1}{2x+1} \\ \frac{2}{2x+1} \\ \end{matrix} \right)$
$y=\frac{4x+1}{2x+1}$
$x=\frac{2}{2x+1}\Leftrightarrow \frac{1}{2}x=\frac{1}{2x+1}$
$\begin{align} \frac{1}{2}x+y &=\frac{1}{2x+1}+\frac{4x+1}{2x+1} \\ &=\frac{4x+2}{2x+1} \\ \frac{1}{2}x+y &=\frac{2(2x+1)}{2x+1}=2 \end{align}$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 2
Empat koin palsu dicampur dengan delapan koin asli. Jika dua koin diambil secara acak, maka peluang terambil satu koin asli dan satu koin palsu adalah …
A. $\frac{1}{2}$ B. $\frac{16}{33}$ C. $\frac{1}{12}$ D. $\frac{1}{16}$ E. $\frac{1}{32}$
Pembahasan:
Dari 4 koin palsu dan 8 koin asli terambil dua koin maka $n(S)={}_{12}{{C}_{2}}=\frac{12!}{2!10!}=66$.
Kejadian A = {terambil 1 koin asli dan 1 koin palsu}, maka $n(A)={}_{8}{{C}_{1}}.{}_{4}{{C}_{1}}=8.4=32$.
$P(A)=\frac{n(A)}{n(S)}=\frac{32}{66}=\frac{16}{33}$
Jawaban: A
Matematika Dasar SBMPTN 2014 No. 3
Jika $f(x)=\frac{x+1}{x-1}$, $x\ne 1$, maka ${{f}^{-1}}\left( \frac{1}{x} \right)$ = …
A. $-f(x)$
B. $-f(-x)$
C. $\frac{1}{f(x)}$
D. $\frac{1}{f(-x)}$
E. $-\frac{1}{f(x)}$
Pembahasan:
$f(x)=\frac{ax+b}{cx+d}\Leftrightarrow {{f}^{-1}}(x)=\frac{-dx+b}{cx-a}$
$f(x)=\frac{x+1}{x-1}\Leftrightarrow {{f}^{-1}}(x)=\frac{x+1}{x-1}$
$\begin{align} {{f}^{-1}}\left( \frac{1}{x} \right) &=\frac{\frac{1}{x}+1}{\frac{1}{x}-1} \\ &=\frac{\frac{1+x}{x}}{\frac{1-x}{x}}=\frac{x+1}{1-x} \\ &=-\left( \frac{x+1}{x-1} \right) \\ {{f}^{-1}}\left( \frac{1}{x} \right) &=-f(x) \end{align}$
Jawaban: A
Matematika Dasar SBMPTN 2014 No. 4
Tiga puluh data mempunyai rata-rata $p$ . Jika rata-rata 20% data diantaranya adalah $p+0,1$. 40% lainnya adalah $p-0,1$, 10% lainnya lagi adalah $p-0,5$, dan rata-rata 30% data sisanya adalah $p+q$, maka $q$ = ….
A. $\frac{1}{5}$ B. $\frac{7}{30}$ C. $\frac{4}{15}$ D. $\frac{3}{10}$ E. $\frac{3}{3}$
Pembahasan:
${{n}_{total}}=30\to {{\bar{x}}_{total}}=p$
${{n}_{1}}=20%.30=6\to {{\bar{x}}_{1}}=p+0,1$
${{n}_{2}}=40%.30=12\to {{\bar{x}}_{2}}=p-0,1$
${{n}_{3}}=10%.30=3\to {{\bar{x}}_{3}}=p-0,5$
${{n}_{4}}=30%.30=9\to {{\bar{x}}_{4}}=p+q$
${{n}_{total}}.{{\bar{x}}_{total}}={{n}_{1}}.{{\bar{x}}_{1}}+{{n}_{2}}.{{\bar{x}}_{2}}+{{n}_{3}}.{{\bar{x}}_{3}}+{{n}_{4}}.{{\bar{x}}_{4}}$
$30p=6(p+0,1)+12(p-0,1)+3(p-0,5)+9(p+q)$
$30p=6p+0,6+12p-1,2+3p-1,5+9p+9q$
$30p=30p+9q-2,1$
$2,1=9q\Leftrightarrow q=\frac{2,1}{9}=\frac{7}{30}$
Jawaban: B
Matematika Dasar SBMPTN 2014 No. 5
Nilai $\frac{1}{2}$ + $({}^{3}log8)({}^{2}log3+{}^{4}log5)$ - $4{}^{9}log45$ adalah …
A. $\frac{3}{2}\log 15$
B. ${}^{3}log225$
C. ${}^{3}log\sqrt{15}$
D. $-{}^{9}log15$
E. $-{}^{3}log15$
Pembahasan:
$\frac{1}{2}$ + $({}^{3}log8)({}^{2}log3+{}^{4}log5)$ - $4{}^{9}log45$
= $\frac{1}{2}$ + $({}^{3}log{{2}^{3}})({}^{2}log3+{}^{{{2}^{2}}}log5)$ - $4.{}^{{{3}^{2}}}log45$
= $\frac{1}{2}$ + $(3.{}^{3}log2)({}^{2}log3+{}^{2}log\sqrt{5})$ - $4.{}^{3}log\sqrt{45}$
= $\frac{1}{2}$ + $3.{}^{3}log2.{}^{2}log3\sqrt{5}$-$4.{}^{3}log3\sqrt{5}$
= ${}^{3}\log {{3}^{\frac{1}{2}}}$ + $3.{}^{3}log3\sqrt{5}$-$4.{}^{3}log3\sqrt{5}$
= ${}^{3}\log \sqrt{3}-{}^{3}log3\sqrt{5}$
= ${}^{3}\log \frac{\sqrt{3}}{3\sqrt{5}}$
= ${}^{3}\log \frac{1}{\sqrt{15}}$
= $-{}^{3}\log \sqrt{15}$
= $-{}^{{{3}^{2}}}\log {{\left( \sqrt{15} \right)}^{2}}$
= $-{}^{9}\log 15$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 6
Jika fungsi $f(x)={{a}^{2}}{{x}^{2}}-12x+{{c}^{2}}$ menyinggung sumbu X di $x=\frac{2}{3}$, maka ${{a}^{2}}-{{c}^{2}}$ = …
A. 1 B. 2 C. 3 D. 5 E. 7
Pembahasan:
$f(x)={{a}^{2}}{{x}^{2}}-12x+{{c}^{2}}$
$f'(x)=2{{a}^{2}}x-12$ menyinggung sumbu X di $x=\frac{2}{3}$, maka:
$f'\left( \frac{2}{3} \right)=0$
$2{{a}^{2}}.\frac{2}{3}-12=0$
$\frac{4}{3}{{a}^{2}}=12\Leftrightarrow {{a}^{2}}=9$
$f(x)={{a}^{2}}{{x}^{2}}-12x+{{c}^{2}}$ menyinggung sumbu X, maka:
D = 0
${{b}^{2}}-4ac=0$
${{12}^{2}}-4.{{a}^{2}}{{c}^{2}}=0$
${{12}^{2}}-4.9.{{c}^{2}}=0$
$144=36{{c}^{2}}\Leftrightarrow {{c}^{2}}=4$
${{a}^{2}}-{{c}^{2}}=9-4=5$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 7
Garis $l$ mempunyai gradien 2. Jika $l$ menyinggung grafik fungsi $f(x)=-{{x}^{2}}+px+1$ di $x=1$, maka persamaan $l$ adalah …
A. y = 2x – 3
B. y = 2x – 1
C. y = 2x
D. y = 2x + 2
E. y = 2x + 4
Pembahasan:
$f(x)=-{{x}^{2}}+px+1$
$f'(x)=-2x+p$ gradiennya di $x=1$ adalah 2, maka:
$f'(1)=2$
$-2.1+p=2\Leftrightarrow p=4$
$f(x)=-{{x}^{2}}+4x+1$
${{x}_{1}}=1\Rightarrow {{y}_{1}}=-{{1}^{2}}+4.1+1=4$
Persamaan garis $l$ di titik (1,4) dengan gradien m = 2 adalah:
$y-{{y}_{1}}=m(x-{{x}_{1}})$
$y-4=2(x-1)\Leftrightarrow y=2x+2$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 8
Semua nilai x yang memenuhi pertidaksamaan ${{2}^{2x+2}}-17({{2}^{x}})+4 < 0$
A. $\frac{1}{2} < x < 2$
B. $\frac{1}{4} < x < 4$
C. $-\frac{1}{4} < x < 2$
D. $0 < x < 2$
E. $-2 < x < 2$
Pembahasan:
${{2}^{2x+2}}-17({{2}^{x}})+4 < 0$
${{2}^{2x}}{{.2}^{2}}-17({{2}^{x}})+4 < 0$
$4{{({{2}^{x}})}^{2}}-17({{2}^{x}})+4 < 0$
Misal: ${{2}^{x}}=p$ maka:
$4{{p}^{2}}-17p+4 < 0$
$(4p-1)(p-4) < 0$
$\frac{1}{4} < p < 4$, ingat: ${{2}^{x}}=p$, maka:
${{2}^{-2}} < {{2}^{x}} < {{2}^{2}}$
$-2 < x < 2$
Jawaban: E
Matematika Dasar SBMPTN 2014 No. 9
Diketahui ${{x}_{1}}$ dan ${{x}_{2}}$ akar-akar persamaan ${{x}^{2}}+3x+p=0$ dengan ${{x}_{1}}$ dan ${{x}_{2}}$ kedua-duanya tidak sama dengan nol. Jika ${{x}_{1}}+{{x}_{2}}$, ${{x}_{1}}.{{x}_{2}}$, dan $x_{1}^{2}x_{2}^{2}$ merupakan 3 suku pertama barisan aritmetika maka $p$ = …
A. -3 B. -1 C. 0 D. 1 E. 3
Pembahasan:
${{x}^{2}}+3x+p=0$ akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$, maka:
${{x}_{1}}+{{x}_{2}}=-3$
${{x}_{1}}.{{x}_{2}}=p$
$x_{1}^{2}x_{2}^{2}={{p}^{2}}$
Barisan aritmetika:
${{x}_{1}}+{{x}_{2}}$, ${{x}_{1}}.{{x}_{2}}$, $x_{1}^{2}x_{2}^{2}$
$-3,p,{{p}^{2}}$, maka:
$2{{U}_{2}}={{U}_{1}}+{{U}_{3}}$
$2p=-3+{{p}^{2}}$
${{p}^{2}}-2p-3=0$
$(p-3)(p+1)=0$
$p=3$ atau $p=-1$
Jawaban: B/E
Matematika Dasar SBMPTN 2014 No. 10
Himpunan penyelesaian pertidaksamaan $\sqrt{{{x}^{2}}-2x} < \sqrt{3x+6}$ adalah …
A. {$x|-1 < x < 6$}
B. {$x|-2 < x \le 0$ atau $x \ge 2$}
C. {$x|x \ge -2$}
D. {$x|-2 < x \le 0$ atau $2 \le x < 6$}
E. {$x|-1 < x \le 0$ atau $2 \le x < 6$}
Pembahasan:
$\sqrt{{{x}^{2}}-2x} < \sqrt{3x+6}$
i)
${{x}^{2}}-2x \ge 0$
$x(x-2) \ge 0$
$x \le 0$ atau $x \ge 2$
ii) $3x+6 \ge 0\Leftrightarrow x \ge -2$
iii)
$\sqrt{{{x}^{2}}-2x} < \sqrt{3x+6}$
${{x}^{2}}-2x < 3x+6$
${{x}^{2}}-5x-6 < 0$
$(x-6)(x+1) < 0$
$-1 < x < 6$
Dari i), ii) dan iii) diperoleh:
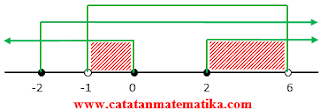
$x|-1 < x \le 0$ atau $2 \le x < 6$
Jawaban: E
Matematika Dasar SBMPTN 2014 No. 11
Jika $\cos x=2\sin x$, maka nilai $\sin x.\cos x$ adalah …
A. $\frac{1}{5}$ B. $\frac{1}{4}$ C. $\frac{1}{3}$ D. $\frac{2}{5}$ E. $\frac{2}{3}$
Pembahasan:
$\cos x=2\sin x$
$\cos x=2\sin x$, bagi dengan $\sin x$
$\frac{\cos x}{\sin x}=2$
$\cot x=\frac{2}{1}=\frac{sa}{de}$
$mi=\sqrt{d{{e}^{2}}+s{{a}^{2}}}$
$mi=\sqrt{{{1}^{2}}+{{2}^{2}}}=\sqrt{5}$
Maka:
$\sin x.\cos x=\frac{de}{mi}.\frac{sa}{mi}=\frac{1}{\sqrt{5}}.\frac{2}{\sqrt{5}}=\frac{2}{5}$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 12
Jumlah suku ke-4 dan suku ke-5 dari suatu barisan aritmetika adalah 55, sedangkan suku ke-9 dikurangi dua kali suku ke-2 bernilai 1. Jumlah tiga suku pertama barisan tersebut adalah …
A. 17 B. 35 C. 37 D. 40 E. 60
Pembahasan:
Barisan Aritmetika: ${{U}_{n}}=a+(n-1)b$
${{U}_{4}}+{{U}_{5}}=55$
$a+3b+a+4b=55\Leftrightarrow 2a+7b=55$
${{U}_{9}}-2{{U}_{2}}=1$
$a+8b-2(a+b)=1\Leftrightarrow -a+6b=1$
$\begin{align} 2a+7b &=55|\times 1 \\ -a+6b & =1|\times 2 \\ \end{align}$
$2a+7b=55$
$-2a+12b=2$
------------------ ( + )
$19b=57\Rightarrow b=3$
Substitusi ke:
$2a+7b=55\Leftrightarrow 2a+7.3=55\Leftrightarrow a=17$
${{S}_{n}}=\frac{n}{2}(2a+(n-1)b)$
${{S}_{3}}=\frac{3}{2}(2a+2b)$
${{S}_{3}}=\frac{3}{2}(2.17+2.3)=60$
Jawaban: E
Matematika Dasar SBMPTN 2014 No. 13
Seorang penjahit akan memuat 2 model pakaian. Dia mempunyai persediaan kain batik 40 meter dan kain polos 15 meter. Model A memerlukan 1 meter kain batik dan 1,5 meter kain polos, sedang model B memerlukan 2 meter kain batik dan 0,5 meter kain polos. Maksimum banyak pakaian yang mungkin dapat dibuat adalah …
A. 10 B. 20 C. 22 D. 25 E. 30
Pembahasan:
Misalkan:
$x$ = banyak pakaian model A
$y$ = banyak pakaian model B
Kain batik: $x+2y\le 40$ | kali 2
Kain polos: $1,5x+0,5y\le 15$| kali 2
Maka:
$2x+4y\le 80$
$3x+y\le 30$
---------------- (+)
$5x+5y\le 110$
$x+y\le 22$
Jadi, jumlah maksimum pakaian yang dapat dibuat adalah 22.
Jawaban: C
Matematika Dasar SBMPTN 2014 No. 14
Jika ${{x}_{1}}$ dan ${{x}_{2}}$ akar-akar persamaan kuadrat ${{x}^{2}}+3x+1=0$, maka persamaan kuadrat dengan akar-akar $2+\frac{{{x}_{2}}}{{{x}_{1}}}$ dan $2+\frac{{{x}_{2}}}{{{x}_{1}}}$ adalah …
A. ${{x}^{2}}-11x+19=0$
B. ${{x}^{2}}+11x+19=0$
C. ${{x}^{2}}-11x-19=0$
D. ${{x}^{2}}-19x+11=0$
E. ${{x}^{2}}+19x+11=0$
Pembahasan:
PK. Awal: ${{x}^{2}}+3x+1=0$ akar-akar ${{x}_{1}}$ dan ${{x}_{2}}$.
${{x}_{1}}+{{x}_{2}}=-3$ dan ${{x}_{1}}.{{x}_{2}}=1$
PK. Baru: akar-akar $2+\frac{{{x}_{2}}}{{{x}_{1}}}$ dan $2+\frac{{{x}_{2}}}{{{x}_{1}}}$
Jumlah akar (J)
$J=2+\frac{{{x}_{2}}}{{{x}_{1}}}+2+\frac{{{x}_{1}}}{{{x}_{2}}}$
$J=4+\frac{x_{2}^{2}+x_{1}^{2}}{{{x}_{1}}.{{x}_{2}}}$
$J=4+\frac{{{({{x}_{1}}+{{x}_{2}})}^{2}}-2{{x}_{1}}.{{x}_{2}}}{{{x}_{1}}.{{x}_{2}}}$
$J=4+\frac{{{(-3)}^{2}}-2.1}{1}$
$J=11$
Hasil kali akar (K)
$K=\left( 2+\frac{{{x}_{2}}}{{{x}_{1}}} \right).\left( 2+\frac{{{x}_{1}}}{{{x}_{2}}} \right)$
$K=4+2\left( \frac{{{x}_{1}}}{{{x}_{2}}}+\frac{{{x}_{2}}}{{{x}_{1}}} \right)+\frac{{{x}_{2}}}{{{x}_{1}}}.\frac{{{x}_{1}}}{{{x}_{2}}}$
$K=4+2.7+1$
$K=19$
PK. Baru:
${{x}^{2}}-Jx+K=0\Leftrightarrow {{x}^{2}}-11x+19=0$
Jawaban: A
Matematika Dasar SBMPTN 2014 No. 15
Agar sistem persamaan:
$\left\{ \begin{matrix} 2x-y-1=0 \\ 4x-y-5=0 \\ ax-y-7=0 \\ \end{matrix} \right.$
Mempunyai penyelesaian, maka nilai $a$ adalah …
A. 3 B. 5 C. 6 D. 7 E. 8
Pembahasan:
$2x-y-1=0$
$4x-y-5=0$
----------------- (-)
$-2x=-4\Leftrightarrow x=2$
Substitusi ke:
$2x-y-1=0$
$2.2-y-1=0\Leftrightarrow 3=y$
Titik $(2,3)$ melalui $ax-y-7=0$ maka:
$a.2-3-7=0\Leftrightarrow 2a=10\Leftrightarrow a=5$
Jawaban: B
Matematika Dasar SBMPTN 2014 No. 1
Jika $\left( \begin{matrix} y \\ x \\ \end{matrix} \right)={{\left( \begin{matrix} 2 & 1 \\ -1 & x \\ \end{matrix} \right)}^{-1}}\left( \begin{matrix} 4 \\ -1 \\ \end{matrix} \right)$ dengan $x\ne -\frac{1}{2}$, maka nilai $\frac{1}{2}x+y$ = …
A. -4 B. -2 C. 0 D. 2 E. 4
Pembahasan:
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)={{\left( \begin{matrix} 2 & 1 \\ -1 & x \\ \end{matrix} \right)}^{-1}}\left( \begin{matrix} 4 \\ -1 \\ \end{matrix} \right)$
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)=\frac{1}{2x+1}\left( \begin{matrix} x & -1 \\ 1 & 2 \\ \end{matrix} \right)\left( \begin{matrix} 4 \\ -1 \\ \end{matrix} \right)$
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)=\frac{1}{2x+1}\left( \begin{matrix} 4x+1 \\ 4-2 \\ \end{matrix} \right)$
$\left( \begin{matrix} y \\ x \\ \end{matrix} \right)=\left( \begin{matrix} \frac{4x+1}{2x+1} \\ \frac{2}{2x+1} \\ \end{matrix} \right)$
$y=\frac{4x+1}{2x+1}$
$x=\frac{2}{2x+1}\Leftrightarrow \frac{1}{2}x=\frac{1}{2x+1}$
$\begin{align} \frac{1}{2}x+y &=\frac{1}{2x+1}+\frac{4x+1}{2x+1} \\ &=\frac{4x+2}{2x+1} \\ \frac{1}{2}x+y &=\frac{2(2x+1)}{2x+1}=2 \end{align}$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 2
Empat koin palsu dicampur dengan delapan koin asli. Jika dua koin diambil secara acak, maka peluang terambil satu koin asli dan satu koin palsu adalah …
A. $\frac{1}{2}$ B. $\frac{16}{33}$ C. $\frac{1}{12}$ D. $\frac{1}{16}$ E. $\frac{1}{32}$
Pembahasan:
Dari 4 koin palsu dan 8 koin asli terambil dua koin maka $n(S)={}_{12}{{C}_{2}}=\frac{12!}{2!10!}=66$.
Kejadian A = {terambil 1 koin asli dan 1 koin palsu}, maka $n(A)={}_{8}{{C}_{1}}.{}_{4}{{C}_{1}}=8.4=32$.
$P(A)=\frac{n(A)}{n(S)}=\frac{32}{66}=\frac{16}{33}$
Jawaban: A
Matematika Dasar SBMPTN 2014 No. 3
Jika $f(x)=\frac{x+1}{x-1}$, $x\ne 1$, maka ${{f}^{-1}}\left( \frac{1}{x} \right)$ = …
A. $-f(x)$
B. $-f(-x)$
C. $\frac{1}{f(x)}$
D. $\frac{1}{f(-x)}$
E. $-\frac{1}{f(x)}$
Pembahasan:
$f(x)=\frac{ax+b}{cx+d}\Leftrightarrow {{f}^{-1}}(x)=\frac{-dx+b}{cx-a}$
$f(x)=\frac{x+1}{x-1}\Leftrightarrow {{f}^{-1}}(x)=\frac{x+1}{x-1}$
$\begin{align} {{f}^{-1}}\left( \frac{1}{x} \right) &=\frac{\frac{1}{x}+1}{\frac{1}{x}-1} \\ &=\frac{\frac{1+x}{x}}{\frac{1-x}{x}}=\frac{x+1}{1-x} \\ &=-\left( \frac{x+1}{x-1} \right) \\ {{f}^{-1}}\left( \frac{1}{x} \right) &=-f(x) \end{align}$
Jawaban: A
Matematika Dasar SBMPTN 2014 No. 4
Tiga puluh data mempunyai rata-rata $p$ . Jika rata-rata 20% data diantaranya adalah $p+0,1$. 40% lainnya adalah $p-0,1$, 10% lainnya lagi adalah $p-0,5$, dan rata-rata 30% data sisanya adalah $p+q$, maka $q$ = ….
A. $\frac{1}{5}$ B. $\frac{7}{30}$ C. $\frac{4}{15}$ D. $\frac{3}{10}$ E. $\frac{3}{3}$
Pembahasan:
${{n}_{total}}=30\to {{\bar{x}}_{total}}=p$
${{n}_{1}}=20%.30=6\to {{\bar{x}}_{1}}=p+0,1$
${{n}_{2}}=40%.30=12\to {{\bar{x}}_{2}}=p-0,1$
${{n}_{3}}=10%.30=3\to {{\bar{x}}_{3}}=p-0,5$
${{n}_{4}}=30%.30=9\to {{\bar{x}}_{4}}=p+q$
${{n}_{total}}.{{\bar{x}}_{total}}={{n}_{1}}.{{\bar{x}}_{1}}+{{n}_{2}}.{{\bar{x}}_{2}}+{{n}_{3}}.{{\bar{x}}_{3}}+{{n}_{4}}.{{\bar{x}}_{4}}$
$30p=6(p+0,1)+12(p-0,1)+3(p-0,5)+9(p+q)$
$30p=6p+0,6+12p-1,2+3p-1,5+9p+9q$
$30p=30p+9q-2,1$
$2,1=9q\Leftrightarrow q=\frac{2,1}{9}=\frac{7}{30}$
Jawaban: B
Matematika Dasar SBMPTN 2014 No. 5
Nilai $\frac{1}{2}$ + $({}^{3}log8)({}^{2}log3+{}^{4}log5)$ - $4{}^{9}log45$ adalah …
A. $\frac{3}{2}\log 15$
B. ${}^{3}log225$
C. ${}^{3}log\sqrt{15}$
D. $-{}^{9}log15$
E. $-{}^{3}log15$
Pembahasan:
$\frac{1}{2}$ + $({}^{3}log8)({}^{2}log3+{}^{4}log5)$ - $4{}^{9}log45$
= $\frac{1}{2}$ + $({}^{3}log{{2}^{3}})({}^{2}log3+{}^{{{2}^{2}}}log5)$ - $4.{}^{{{3}^{2}}}log45$
= $\frac{1}{2}$ + $(3.{}^{3}log2)({}^{2}log3+{}^{2}log\sqrt{5})$ - $4.{}^{3}log\sqrt{45}$
= $\frac{1}{2}$ + $3.{}^{3}log2.{}^{2}log3\sqrt{5}$-$4.{}^{3}log3\sqrt{5}$
= ${}^{3}\log {{3}^{\frac{1}{2}}}$ + $3.{}^{3}log3\sqrt{5}$-$4.{}^{3}log3\sqrt{5}$
= ${}^{3}\log \sqrt{3}-{}^{3}log3\sqrt{5}$
= ${}^{3}\log \frac{\sqrt{3}}{3\sqrt{5}}$
= ${}^{3}\log \frac{1}{\sqrt{15}}$
= $-{}^{3}\log \sqrt{15}$
= $-{}^{{{3}^{2}}}\log {{\left( \sqrt{15} \right)}^{2}}$
= $-{}^{9}\log 15$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 6
Jika fungsi $f(x)={{a}^{2}}{{x}^{2}}-12x+{{c}^{2}}$ menyinggung sumbu X di $x=\frac{2}{3}$, maka ${{a}^{2}}-{{c}^{2}}$ = …
A. 1 B. 2 C. 3 D. 5 E. 7
Pembahasan:
$f(x)={{a}^{2}}{{x}^{2}}-12x+{{c}^{2}}$
$f'(x)=2{{a}^{2}}x-12$ menyinggung sumbu X di $x=\frac{2}{3}$, maka:
$f'\left( \frac{2}{3} \right)=0$
$2{{a}^{2}}.\frac{2}{3}-12=0$
$\frac{4}{3}{{a}^{2}}=12\Leftrightarrow {{a}^{2}}=9$
$f(x)={{a}^{2}}{{x}^{2}}-12x+{{c}^{2}}$ menyinggung sumbu X, maka:
D = 0
${{b}^{2}}-4ac=0$
${{12}^{2}}-4.{{a}^{2}}{{c}^{2}}=0$
${{12}^{2}}-4.9.{{c}^{2}}=0$
$144=36{{c}^{2}}\Leftrightarrow {{c}^{2}}=4$
${{a}^{2}}-{{c}^{2}}=9-4=5$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 7
Garis $l$ mempunyai gradien 2. Jika $l$ menyinggung grafik fungsi $f(x)=-{{x}^{2}}+px+1$ di $x=1$, maka persamaan $l$ adalah …
A. y = 2x – 3
B. y = 2x – 1
C. y = 2x
D. y = 2x + 2
E. y = 2x + 4
Pembahasan:
$f(x)=-{{x}^{2}}+px+1$
$f'(x)=-2x+p$ gradiennya di $x=1$ adalah 2, maka:
$f'(1)=2$
$-2.1+p=2\Leftrightarrow p=4$
$f(x)=-{{x}^{2}}+4x+1$
${{x}_{1}}=1\Rightarrow {{y}_{1}}=-{{1}^{2}}+4.1+1=4$
Persamaan garis $l$ di titik (1,4) dengan gradien m = 2 adalah:
$y-{{y}_{1}}=m(x-{{x}_{1}})$
$y-4=2(x-1)\Leftrightarrow y=2x+2$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 8
Semua nilai x yang memenuhi pertidaksamaan ${{2}^{2x+2}}-17({{2}^{x}})+4 < 0$
A. $\frac{1}{2} < x < 2$
B. $\frac{1}{4} < x < 4$
C. $-\frac{1}{4} < x < 2$
D. $0 < x < 2$
E. $-2 < x < 2$
Pembahasan:
${{2}^{2x+2}}-17({{2}^{x}})+4 < 0$
${{2}^{2x}}{{.2}^{2}}-17({{2}^{x}})+4 < 0$
$4{{({{2}^{x}})}^{2}}-17({{2}^{x}})+4 < 0$
Misal: ${{2}^{x}}=p$ maka:
$4{{p}^{2}}-17p+4 < 0$
$(4p-1)(p-4) < 0$
$\frac{1}{4} < p < 4$, ingat: ${{2}^{x}}=p$, maka:
${{2}^{-2}} < {{2}^{x}} < {{2}^{2}}$
$-2 < x < 2$
Jawaban: E
Matematika Dasar SBMPTN 2014 No. 9
Diketahui ${{x}_{1}}$ dan ${{x}_{2}}$ akar-akar persamaan ${{x}^{2}}+3x+p=0$ dengan ${{x}_{1}}$ dan ${{x}_{2}}$ kedua-duanya tidak sama dengan nol. Jika ${{x}_{1}}+{{x}_{2}}$, ${{x}_{1}}.{{x}_{2}}$, dan $x_{1}^{2}x_{2}^{2}$ merupakan 3 suku pertama barisan aritmetika maka $p$ = …
A. -3 B. -1 C. 0 D. 1 E. 3
Pembahasan:
${{x}^{2}}+3x+p=0$ akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$, maka:
${{x}_{1}}+{{x}_{2}}=-3$
${{x}_{1}}.{{x}_{2}}=p$
$x_{1}^{2}x_{2}^{2}={{p}^{2}}$
Barisan aritmetika:
${{x}_{1}}+{{x}_{2}}$, ${{x}_{1}}.{{x}_{2}}$, $x_{1}^{2}x_{2}^{2}$
$-3,p,{{p}^{2}}$, maka:
$2{{U}_{2}}={{U}_{1}}+{{U}_{3}}$
$2p=-3+{{p}^{2}}$
${{p}^{2}}-2p-3=0$
$(p-3)(p+1)=0$
$p=3$ atau $p=-1$
Jawaban: B/E
Matematika Dasar SBMPTN 2014 No. 10
Himpunan penyelesaian pertidaksamaan $\sqrt{{{x}^{2}}-2x} < \sqrt{3x+6}$ adalah …
A. {$x|-1 < x < 6$}
B. {$x|-2 < x \le 0$ atau $x \ge 2$}
C. {$x|x \ge -2$}
D. {$x|-2 < x \le 0$ atau $2 \le x < 6$}
E. {$x|-1 < x \le 0$ atau $2 \le x < 6$}
Pembahasan:
$\sqrt{{{x}^{2}}-2x} < \sqrt{3x+6}$
i)
${{x}^{2}}-2x \ge 0$
$x(x-2) \ge 0$
$x \le 0$ atau $x \ge 2$
ii) $3x+6 \ge 0\Leftrightarrow x \ge -2$
iii)
$\sqrt{{{x}^{2}}-2x} < \sqrt{3x+6}$
${{x}^{2}}-2x < 3x+6$
${{x}^{2}}-5x-6 < 0$
$(x-6)(x+1) < 0$
$-1 < x < 6$
Dari i), ii) dan iii) diperoleh:

$x|-1 < x \le 0$ atau $2 \le x < 6$
Jawaban: E
Matematika Dasar SBMPTN 2014 No. 11
Jika $\cos x=2\sin x$, maka nilai $\sin x.\cos x$ adalah …
A. $\frac{1}{5}$ B. $\frac{1}{4}$ C. $\frac{1}{3}$ D. $\frac{2}{5}$ E. $\frac{2}{3}$
Pembahasan:
$\cos x=2\sin x$
$\cos x=2\sin x$, bagi dengan $\sin x$
$\frac{\cos x}{\sin x}=2$
$\cot x=\frac{2}{1}=\frac{sa}{de}$
$mi=\sqrt{d{{e}^{2}}+s{{a}^{2}}}$
$mi=\sqrt{{{1}^{2}}+{{2}^{2}}}=\sqrt{5}$
Maka:
$\sin x.\cos x=\frac{de}{mi}.\frac{sa}{mi}=\frac{1}{\sqrt{5}}.\frac{2}{\sqrt{5}}=\frac{2}{5}$
Jawaban: D
Matematika Dasar SBMPTN 2014 No. 12
Jumlah suku ke-4 dan suku ke-5 dari suatu barisan aritmetika adalah 55, sedangkan suku ke-9 dikurangi dua kali suku ke-2 bernilai 1. Jumlah tiga suku pertama barisan tersebut adalah …
A. 17 B. 35 C. 37 D. 40 E. 60
Pembahasan:
Barisan Aritmetika: ${{U}_{n}}=a+(n-1)b$
${{U}_{4}}+{{U}_{5}}=55$
$a+3b+a+4b=55\Leftrightarrow 2a+7b=55$
${{U}_{9}}-2{{U}_{2}}=1$
$a+8b-2(a+b)=1\Leftrightarrow -a+6b=1$
$\begin{align} 2a+7b &=55|\times 1 \\ -a+6b & =1|\times 2 \\ \end{align}$
$2a+7b=55$
$-2a+12b=2$
------------------ ( + )
$19b=57\Rightarrow b=3$
Substitusi ke:
$2a+7b=55\Leftrightarrow 2a+7.3=55\Leftrightarrow a=17$
${{S}_{n}}=\frac{n}{2}(2a+(n-1)b)$
${{S}_{3}}=\frac{3}{2}(2a+2b)$
${{S}_{3}}=\frac{3}{2}(2.17+2.3)=60$
Jawaban: E
Matematika Dasar SBMPTN 2014 No. 13
Seorang penjahit akan memuat 2 model pakaian. Dia mempunyai persediaan kain batik 40 meter dan kain polos 15 meter. Model A memerlukan 1 meter kain batik dan 1,5 meter kain polos, sedang model B memerlukan 2 meter kain batik dan 0,5 meter kain polos. Maksimum banyak pakaian yang mungkin dapat dibuat adalah …
A. 10 B. 20 C. 22 D. 25 E. 30
Pembahasan:
Misalkan:
$x$ = banyak pakaian model A
$y$ = banyak pakaian model B
Kain batik: $x+2y\le 40$ | kali 2
Kain polos: $1,5x+0,5y\le 15$| kali 2
Maka:
$2x+4y\le 80$
$3x+y\le 30$
---------------- (+)
$5x+5y\le 110$
$x+y\le 22$
Jadi, jumlah maksimum pakaian yang dapat dibuat adalah 22.
Jawaban: C
Matematika Dasar SBMPTN 2014 No. 14
Jika ${{x}_{1}}$ dan ${{x}_{2}}$ akar-akar persamaan kuadrat ${{x}^{2}}+3x+1=0$, maka persamaan kuadrat dengan akar-akar $2+\frac{{{x}_{2}}}{{{x}_{1}}}$ dan $2+\frac{{{x}_{2}}}{{{x}_{1}}}$ adalah …
A. ${{x}^{2}}-11x+19=0$
B. ${{x}^{2}}+11x+19=0$
C. ${{x}^{2}}-11x-19=0$
D. ${{x}^{2}}-19x+11=0$
E. ${{x}^{2}}+19x+11=0$
Pembahasan:
PK. Awal: ${{x}^{2}}+3x+1=0$ akar-akar ${{x}_{1}}$ dan ${{x}_{2}}$.
${{x}_{1}}+{{x}_{2}}=-3$ dan ${{x}_{1}}.{{x}_{2}}=1$
PK. Baru: akar-akar $2+\frac{{{x}_{2}}}{{{x}_{1}}}$ dan $2+\frac{{{x}_{2}}}{{{x}_{1}}}$
Jumlah akar (J)
$J=2+\frac{{{x}_{2}}}{{{x}_{1}}}+2+\frac{{{x}_{1}}}{{{x}_{2}}}$
$J=4+\frac{x_{2}^{2}+x_{1}^{2}}{{{x}_{1}}.{{x}_{2}}}$
$J=4+\frac{{{({{x}_{1}}+{{x}_{2}})}^{2}}-2{{x}_{1}}.{{x}_{2}}}{{{x}_{1}}.{{x}_{2}}}$
$J=4+\frac{{{(-3)}^{2}}-2.1}{1}$
$J=11$
Hasil kali akar (K)
$K=\left( 2+\frac{{{x}_{2}}}{{{x}_{1}}} \right).\left( 2+\frac{{{x}_{1}}}{{{x}_{2}}} \right)$
$K=4+2\left( \frac{{{x}_{1}}}{{{x}_{2}}}+\frac{{{x}_{2}}}{{{x}_{1}}} \right)+\frac{{{x}_{2}}}{{{x}_{1}}}.\frac{{{x}_{1}}}{{{x}_{2}}}$
$K=4+2.7+1$
$K=19$
PK. Baru:
${{x}^{2}}-Jx+K=0\Leftrightarrow {{x}^{2}}-11x+19=0$
Jawaban: A
Matematika Dasar SBMPTN 2014 No. 15
Agar sistem persamaan:
$\left\{ \begin{matrix} 2x-y-1=0 \\ 4x-y-5=0 \\ ax-y-7=0 \\ \end{matrix} \right.$
Mempunyai penyelesaian, maka nilai $a$ adalah …
A. 3 B. 5 C. 6 D. 7 E. 8
Pembahasan:
$2x-y-1=0$
$4x-y-5=0$
----------------- (-)
$-2x=-4\Leftrightarrow x=2$
Substitusi ke:
$2x-y-1=0$
$2.2-y-1=0\Leftrightarrow 3=y$
Titik $(2,3)$ melalui $ax-y-7=0$ maka:
$a.2-3-7=0\Leftrightarrow 2a=10\Leftrightarrow a=5$
Jawaban: B
Artikel Terkait:
|

Post a Comment for "Pembahasan SBMPTN 2014 Matematika Dasar Kode 614"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.