Matematika Dasar SNMPTN/SBMPTN 2011 Kode 171 [Soal + Pembahasan]
Eits.... tunggu dulu. Buat adik-adik pejuang masuk PTN (Perguruan Tinggi Negeri) alangkah baiknya sebelum melihat pembahasan ini lebih lanjut saya rekomendasikan agar kalian download terlebih dahulu soalnya, setelah di download silahkan dijawab secara mandiri, setelah selesai bolehlah melirik pembahasan ini. Oh iya bapak/ibu guru baik di sekolah maupun yang memberi les privat juga boleh menggunakan soal ini sebagai bahan belajar.
Matematika Dasar SBMPTN 2011 No. 1
Jika $6({{3}^{40}})({}^{2}\log a)+{{3}^{41}}({}^{2}\log a)={{3}^{43}}$, maka nilai a adalah …
A. $\frac{1}{8}$ B. $\frac{1}{4}$ C. 4 D. 8 E. 16
Pembahasan:
$6({{3}^{40}})({}^{2}\log a)+{{3}^{41}}({}^{2}\log a)={{3}^{43}}$
${{2.3.3}^{40}}.{}^{2}\log a+{{3}^{41}}.{}^{2}\log a={{3}^{43}}$
${{2.3}^{41}}.{}^{2}\log a+{{3}^{41}}.{}^{2}\log a={{3}^{43}}$
$(2+1){{3}^{41}}.{}^{2}\log a={{3}^{43}}$
${{3.3}^{41}}.{}^{2}\log a={{3}^{43}}$
${{3}^{42}}.{}^{2}\log a={{3}^{43}}$
${}^{2}\log a=\frac{{{3}^{43}}}{{{3}^{42}}}$
${}^{2}\log a=3$
$a={{2}^{3}}=8$
Jawaban: D
Matematika Dasar SBMPTN 2011 No. 2
Jika 2 adalah satu-satunya akar persamaan kuadrat $\frac{1}{4}{{x}^{2}}+bx+a=0$, maka nilai $a+b$ adalah …
A. 32 B. 2 C. 0 D. -2 E. -32
Pembahasan:
$\frac{1}{4}{{x}^{2}}+bx+a=0$, ${{x}_{1}}={{x}_{2}}=2$ maka:
$\frac{1}{4}{{.2}^{2}}+b.2+a=0$
$a+2b=-1$
${{x}_{1}}+{{x}_{2}}=4$
$\frac{-b}{\frac{1}{4}}=4$
$-b=1\Leftrightarrow b=-1$
Substitusi ke:
$a+2b=-1$
$a+2(-1)=-1\Leftrightarrow a=1$
$a+b=1-1=0$
Jawaban: C
Matematika Dasar SBMPTN 2011 No. 3
Bangun berikut adalah suatu persegi.
Jika luas persegi A, B dan C berturut-turut adalah 16, 36, dan 9, maka luas daerah yang di arsir adalah …
A. 61 B. 80 C. 82 D. 87 E. 88
Pembahasan:
Perhatikan gambar berikut:
Luas daerah yang di arsir adalah:
${{L}_{arsir}}={{L}_{total}}-{{L}_{A}}-{{L}_{B}}-{{L}_{D}}$
${{L}_{arsir}}={{13}^{2}}-16-36-\frac{6.7}{2}$
${{L}_{arsir}}=87$
Jawaban: D
Matematika Dasar SBMPTN 2011 No. 4
Jika $\bar{p}$ adalah negasi dari $p$ maka kesimpulan dari pernyataan-pernyataan $p\Rightarrow \bar{q}$ dan $q\vee \bar{r}$ adalah …
A. $r\vee p$
B. $r\wedge p$
C. $\bar{p}\vee \bar{r}$
D. $r\vee \bar{q}$
E. $\bar{q}\Rightarrow p$
Pembahasan:
$p\Rightarrow \bar{q}$ dan $q\vee \bar{r}$
$q\vee \bar{r}$ ekuivalen dengan $\bar{q}\Rightarrow \bar{r}$
Silogisme:
P1: $p\Rightarrow \bar{q}$
P2: $\bar{q}\Rightarrow \bar{r}$
K: $p\Rightarrow \bar{r}$ ekuivalen dengan $\bar{p}\vee \bar{r}$
Jawaban: C
Matematika Dasar SBMPTN 2011 No. 1
Jika $6({{3}^{40}})({}^{2}\log a)+{{3}^{41}}({}^{2}\log a)={{3}^{43}}$, maka nilai a adalah …
A. $\frac{1}{8}$ B. $\frac{1}{4}$ C. 4 D. 8 E. 16
Pembahasan:
$6({{3}^{40}})({}^{2}\log a)+{{3}^{41}}({}^{2}\log a)={{3}^{43}}$
${{2.3.3}^{40}}.{}^{2}\log a+{{3}^{41}}.{}^{2}\log a={{3}^{43}}$
${{2.3}^{41}}.{}^{2}\log a+{{3}^{41}}.{}^{2}\log a={{3}^{43}}$
$(2+1){{3}^{41}}.{}^{2}\log a={{3}^{43}}$
${{3.3}^{41}}.{}^{2}\log a={{3}^{43}}$
${{3}^{42}}.{}^{2}\log a={{3}^{43}}$
${}^{2}\log a=\frac{{{3}^{43}}}{{{3}^{42}}}$
${}^{2}\log a=3$
$a={{2}^{3}}=8$
Jawaban: D
Matematika Dasar SBMPTN 2011 No. 2
Jika 2 adalah satu-satunya akar persamaan kuadrat $\frac{1}{4}{{x}^{2}}+bx+a=0$, maka nilai $a+b$ adalah …
A. 32 B. 2 C. 0 D. -2 E. -32
Pembahasan:
$\frac{1}{4}{{x}^{2}}+bx+a=0$, ${{x}_{1}}={{x}_{2}}=2$ maka:
$\frac{1}{4}{{.2}^{2}}+b.2+a=0$
$a+2b=-1$
${{x}_{1}}+{{x}_{2}}=4$
$\frac{-b}{\frac{1}{4}}=4$
$-b=1\Leftrightarrow b=-1$
Substitusi ke:
$a+2b=-1$
$a+2(-1)=-1\Leftrightarrow a=1$
$a+b=1-1=0$
Jawaban: C
Matematika Dasar SBMPTN 2011 No. 3
Bangun berikut adalah suatu persegi.
Jika luas persegi A, B dan C berturut-turut adalah 16, 36, dan 9, maka luas daerah yang di arsir adalah …
A. 61 B. 80 C. 82 D. 87 E. 88
Pembahasan:
Perhatikan gambar berikut:
Luas daerah yang di arsir adalah:
${{L}_{arsir}}={{L}_{total}}-{{L}_{A}}-{{L}_{B}}-{{L}_{D}}$
${{L}_{arsir}}={{13}^{2}}-16-36-\frac{6.7}{2}$
${{L}_{arsir}}=87$
Jawaban: D
Matematika Dasar SBMPTN 2011 No. 4
Jika $\bar{p}$ adalah negasi dari $p$ maka kesimpulan dari pernyataan-pernyataan $p\Rightarrow \bar{q}$ dan $q\vee \bar{r}$ adalah …
A. $r\vee p$
B. $r\wedge p$
C. $\bar{p}\vee \bar{r}$
D. $r\vee \bar{q}$
E. $\bar{q}\Rightarrow p$
Pembahasan:
$p\Rightarrow \bar{q}$ dan $q\vee \bar{r}$
$q\vee \bar{r}$ ekuivalen dengan $\bar{q}\Rightarrow \bar{r}$
Silogisme:
P1: $p\Rightarrow \bar{q}$
P2: $\bar{q}\Rightarrow \bar{r}$
K: $p\Rightarrow \bar{r}$ ekuivalen dengan $\bar{p}\vee \bar{r}$
Jawaban: C
Matematika Dasar SBMPTN 2011 No. 5
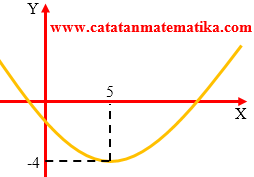
Jika grafik fungsi kuadrat $f(x)=a{{x}^{2}}+bx+c$ dengan puncak $(5,-4)$ memotong sumbu X positif dan sumbu X negatif, maka …
A. $a-c > 0$
B. $a+c < 0$
C. $a+c = 0$
D. $a+c > 0$
E. $a-c < 0$
Pembahasan:
Jika grafik fungsi kuadrat $f(x)=a{{x}^{2}}+bx+c$ dengan puncak $(5,-4)$ memotong sumbu X positif dan sumbu X negatif, maka …
A. $a-c > 0$
B. $a+c < 0$
C. $a+c = 0$
D. $a+c > 0$
E. $a-c < 0$
Pembahasan:
Kurva terbuka ke bawah maka a > 0
Kurva memotong sumbu Y negatif, maka c < 0
sehingga a – c > 0
Jawaban: A
Matematika Dasar SBMPTN 2011 No. 6
Semua nilai $x$ yang memenuhi $\frac{{{x}^{2}}-x+3}{(2{{x}^{2}}-5x-3)({{x}^{2}}+1)}\le 0$ adalah …
A. $-\frac{1}{2} < x < 3$
B. $-3\le x < \frac{1}{2}$
C. $x\le -\frac{1}{2}$ atau $x\ge 3$
D. $x < -\frac{1}{2}$ atau $x > 3$
E. $x < -3$ atau $x\ge \frac{1}{2}$
Pembahasan:
${{x}^{2}}-x+3 > 0$, sebab Definit positif a > 0 dan D < 0)
${{x}^{2}}+3 > 0$, sebab Definit positif a > 0 dan D < 0)
Akibatnya,
$\frac{{{x}^{2}}-x+3}{(2{{x}^{2}}-5x-3)({{x}^{2}}+1)}\le 0$
Karena pembilang positif maka penyebutnya haruslah negatif supaya memenuhi pertidaksamaan tersebut, yaitu:
$2{{x}^{2}}-5x-3 < 0$
$(2x+1)(x-3) < 0$
pembuat nol:
$x=-\frac{1}{2}$ dan $x = 3$, maka:
$-\frac{1}{2} < x < 3$
Jawaban: A
Matematika Dasar SBMPTN 2011 No. 7
Sistem persamaan linier $\left\{ \begin{matrix} x+y=3 \\ -x+3y=1 \\ ax+4by=4 \\ \end{matrix} \right.$ mempunyai penyelesaian, jika nilai $a+2b$ adalah …
A. 4 B. 2 C. -1 D. 0 E. -2
Penyelesaian:
$\begin{align} & x+y=3 \\ & -x+3y=1 \end{align}$
-------------- +
4y = 4
y = 1 dan x = 2
sehingga titik (2,1) dilalui oleh garis:
ax + 4by = 4
2a + 4b = 4
a + 2b = 2
Jawaban: B
Matematika Dasar SBMPTN 2011 No. 8
Nilai ${{\cos }^{2}}({{30}^{o}})+{{\cos }^{2}}({{40}^{o}})+{{\cos }^{2}}({{50}^{o}})+{{\cos }^{2}}({{60}^{o}})$ adalah ….
A. 2 B. $\frac{3}{2}$ C. 1 D. $\frac{1}{2}$ E. 0
Pembahasan:
${{\cos }^{2}}({{30}^{o}})+{{\cos }^{2}}({{40}^{o}})+{{\cos }^{2}}({{50}^{o}})+{{\cos }^{2}}({{60}^{o}})$
$={{\cos }^{2}}({{90}^{o}}-{{60}^{o}})+{{\cos }^{2}}({{90}^{o}}-{{40}^{o}})+{{\cos }^{2}}{{50}^{o}}+{{\cos }^{2}}{{60}^{o}}$
$={{\sin }^{2}}{{60}^{o}}+{{\sin }^{2}}{{50}^{o}}+{{\cos }^{2}}{{50}^{o}}+{{\cos }^{2}}{{60}^{o}}$
$={{\sin }^{2}}{{60}^{o}}+{{\cos }^{2}}{{60}^{o}}+{{\sin }^{2}}{{50}^{o}}+{{\cos }^{2}}{{50}^{o}}$
$=1+1=2$
Jawaban: A
Matematika Dasar SBMPTN 2011 No. 9
Diagram berikut menunjukkan persentase kelulusan siswa tiga sekolah selama empat tahun.
Berdasarkan diagram di samping, pernyataan berikut yang benar adalah …
A. rata-rata persentase kelulusan sekolah B terbaik.
B. persentase kelulusan sekolah B selalu berada di posisi kedua.
C. persentase kelulusan sekolah B selalu lebih baik daripada sekolah A.
D. persentase kelulusan sekolah C selalu lebih baik daripada sekolah B.
E. persentase kelulusan sekolah B selalu lebih baik daripada tahun sebelumnya.
Pembahasan:
Untuk kelas B: persentase kelulusan tahun ke-4 > tahun ke-3 > tahun ke-2 > tahun ke-1
Jawaban: E
Matematika Dasar SBMPTN 2011 No. 10
Jika $f(x)=x+2$ dan $g(x)=\frac{x}{x+5}$, maka nilai $({{g}^{-1}}of)(4)$ adalah …
A. -8 B. -6 C. -2 D. 4 E. 6
Pembahasan:
Misal:
$({{g}^{-1}}of)(4)=a=?$
$({{g}^{-1}}of)(4)={{g}^{-1}}(f(4))$
$a={{g}^{-1}}(4+2)$
$a={{g}^{-1}}(6)$
$g(a)=6$
$\frac{a}{a+5}=6$
$a=6a+30\Leftrightarrow -5a=30\Leftrightarrow a=-6$
Jawaban: B
Matematika Dasar SBMPTN 2011 No. 11
Fungsi $f(x,y)=cx+4y$ dengan kendala $2x+y\ge 10$, $x+2y\ge 8$, $x\ge 0$, dan $y\ge 0$ mencapai minimum di (4,2) jika …
A. $c\le -8$ atau $c\ge -2$
B. $c\le 2$ atau $c\ge 8$
C. $-2\le x\le 8$
D. $2\le x\le 8$
E. $2\le c\le 10$
Pembahasan:
$2x+y\ge 10\Rightarrow {{m}_{1}}=-2$
$x+2y\ge 8\Rightarrow {{m}_{2}}=-\frac{1}{2}$
$f(x,y)=cx+4y\Rightarrow {{m}_{f}}=-\frac{c}{4}$
Agar nilai minimum ada di titik potong (4,2), maka:
${{m}_{1}}\le {{m}_{f}}\le {{m}_{2}}$
$-2\le -\frac{c}{4}\le -\frac{1}{2}$
$8\ge c\ge 2\Leftrightarrow 2\le c\le 8$
Jawaban: D
Matematika Dasar SBMPTN 2011 No. 12
Jika A adalah matriks $2\times 2$ yang memenuhi $A\left( \begin{matrix} 2 \\ 1 \\ \end{matrix} \right)=\left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right)$ dan $A\left( \begin{matrix} 4 \\ 6 \\ \end{matrix} \right)=\left( \begin{matrix} 0 \\ 2 \\ \end{matrix} \right)$, maka hasil kali $A\left( \begin{matrix} 4 & 2 \\ 2 & 3 \\ \end{matrix} \right)$ adalah …
A. $\left( \begin{matrix} 1 & 0 \\ 0 & 2 \\ \end{matrix} \right)$
B. $\left( \begin{matrix} 2 & 0 \\ 0 & 2 \\ \end{matrix} \right)$
C. $\left( \begin{matrix} 2 & 0 \\ 0 & 1 \\ \end{matrix} \right)$
D. $\left( \begin{matrix} 0 & 1 \\ 2 & 0 \\ \end{matrix} \right)$
E. $\left( \begin{matrix} 0 & 2 \\ 1 & 0 \\ \end{matrix} \right)$
Pembahasan:
$A\left( \begin{matrix} 2 \\ 1 \\ \end{matrix} \right)=\left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right)\Rightarrow A\left( \begin{matrix} 4 \\ 2 \\ \end{matrix} \right)=\left( \begin{matrix} 2 \\ 0 \\ \end{matrix} \right)$
$A\left( \begin{matrix} 4 \\ 6 \\ \end{matrix} \right)=\left( \begin{matrix} 0 \\ 2 \\ \end{matrix} \right)\Rightarrow A\left( \begin{matrix} 2 \\ 3 \\ \end{matrix} \right)=\left( \begin{matrix} 0 \\ 1 \\ \end{matrix} \right)$
Digabungkan menjadi:
$A\left( \begin{matrix} 4 & 2 \\ 2 & 3 \\ \end{matrix} \right)=\left( \begin{matrix} 2 & 0 \\ 0 & 1 \\ \end{matrix} \right)$
Jawaban: C
Matematika Dasar SBMPTN 2011 No. 13
Tiga bilangan bulat positif membentuk barisan aritmetika dengan beda 16. Jika bilangan yang terkecil ditambah 7 dan bilangan yang terbesar ditambah 2, maka diperoleh barisan geometri. Jumlah ketiga bilangan tersebut adalah …
A. 56 B. 54 C. 52 D. 50 E. 48
Pembahasan:
Deret Aritmetika (DA):
a, a + 16, a + 32
Deret Geometri:
a + 7, a + 16, a + 34
$\frac{{{U}_{2}}}{{{U}_{1}}}=\frac{{{U}_{3}}}{{{U}_{2}}}$
$\frac{a+16}{a+7}=\frac{a+34}{a+16}$
${{a}^{2}}+32a+256={{a}^{2}}+41a+238$
$32a-41a=238-256$
$-9a=-18$
$a=2$
DA:
a, a + 16, a + 32
2, 18, 34
2 + 18 + 34 = 54
Jawaban: B
Matematika Dasar SBMPTN 2011 No. 14
Jika jumlah 10 suku pertama suatu deret aritmetika adalah 220 dan jumlah 2 suku berturut-turut berikutnya adalah -4, maka jumlah 2 suku pertama deret itu adalah …
A. 36 B. 40 C. 44 D. 72 E. 76
Pembahasan:
Deret Aritmetika:
${{S}_{n}}=\frac{n}{2}\left( 2a+(n-1)b \right)$
${{S}_{10}}=220$
$\frac{10}{2}\left( 2a+9b \right)=220$
$2a+9b=44$ …. (1)
Jumlah dua suku berikutnya -4, maka:
${{U}_{11}}+{{U}_{12}}=-4$
$a+10b+a+11b=-4$
$2a+21b=-4$…. (2)
$2a+9b=44$ …. (1)
------------------------- (-)
$12b=-48$
$b=-4$
$2a+9b=44\Leftrightarrow 2a+9(-4)=44\Leftrightarrow a=40$
$\begin{align} & {{U}_{1}}+{{U}_{2}}=a+(a+b) \\ & =2a+b \\ & =2.40-4 \\ & =76 \end{align}$
Jawaban: E
Matematika Dasar SBMPTN 2011 No. 15
Karyawan pada suatu perusahaan dibedakan menjadi tiga golongan. Karyawan golongan A akan memperoleh gaji per bulan sebesar sepertiga dari gaji karyawan B, sedangkan karyawan golongan C dibayar per bulan sebesar setengah dari gaji karyawan golongan B. penghasilan karyawan golongan C selama 4 bulan akan sama dengan penghasilan karyawan golongan A selama …
A. $\frac{8}{3}$ bulan
B. 3 bulan
C. 4 bulan
D. $\frac{14}{3}$ bulan
E. 6 bulan
Pembahasan:
$A=\frac{1}{3}B\Leftrightarrow B=3A$
$C=\frac{1}{2}B\Leftrightarrow B=2C$
Sehingga:
$3A=2c\Rightarrow C=\frac{3}{2}A$ (untuk satu bulan)
Untuk 4 bulan:
$4C=4.\frac{3}{2}A\Leftrightarrow 4C=6A$
Jawaban: E
Demikianlah Soal dan Pembahasan Matematika Dasar SBMPTN 2011 ini saya persembahkan, kiranya bermanfaat bagi kita semua. Amin.
Demikianlah Soal dan Pembahasan Matematika Dasar SBMPTN 2011 ini saya persembahkan, kiranya bermanfaat bagi kita semua. Amin.
Artikel Terkait:
|
Semoga postingan: Matematika Dasar SNMPTN/SBMPTN 2011 Kode 171 [Soal + Pembahasan] ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Matematika Dasar SNMPTN/SBMPTN 2011 Kode 171 [Soal + Pembahasan]"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.