Polinomial 5. Menentukan Akar-akar Persamaan Suku Banyak

A. Persamaan Suku Banyak

Bentuk umum persamaan suku banyak adalah:
$a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_1x+a_0=0$
$a_n\ne 0$ dan $n$ bilangan asli.

Contoh:
1. $x^3+x^2-10x+8=0$
2. $4x^3-16x^2-x+4=0$
3. $x^4+4x^3+2x^2-4x-3=0$

B. Pengertian Akar Persamaan Suku Banyak

Akar-akar persamaan suku banyak adalah nilai variabel yang memenuhi persamaan suku banyak. Jika $x=k$ akar suatu persamaan maka $(x-k)$ merupakan faktor dari persamaan tersebut.

Contoh:
Manakah yang merupakan akar persamaan suku banyak $x^3+3x^2-x-3=0$ untuk nilai $x$ berikut:
a. $x=3$
b. $x=1$
c. $x=-1$
d. $x=-3$
Penyelesaian:
a. Substitusi $x=1$ ke persamaan $x^3+3x^2-x-3=0$ maka:
$\begin{align}x^3+3x^2-x-3 &= 0 \\ 1^3+3.1^2-1-3 &= 0 \\ 1+3-1-3 &= 0 \\ 0 &= 0\,(benar) \end{align}$
Jadi, $x=1$ adalah akar dari persamaan $x^3+3x^2-x-3=0$.

b. Substitusi $x=-1$ ke persamaan $x^3+3x^2-x-3=0$ maka:
$\begin{align}x^3+3x^2-x-3 &= 0 \\ (-1)^3+3(-1)^2-(-1)-3 &= 0 \\ -1+3+1-3 &= 0 \\ 0 &= 0\,(benar) \end{align}$
Jadi, $x=-1$ adalah akar dari persamaan $x^3+3x^2-x-3=0$.

c. Substitusi $x=3$ ke persamaan $x^3+3x^2-x-3=0$ maka:
$\begin{align}x^3+3x^2-x-3 &= 0 \\ 3^3+3.3^2-3-3 &= 0 \\ 27+27-3-3 &= 0 \\ 48 &= 0\,(salah) \end{align}$
Jadi, $x=3$ bukan akar dari persamaan $x^3+3x^2-x-3=0$.

d. Substitusi $x=-3$ ke persamaan $x^3+3x^2-x-3=0$ maka:
$\begin{align}x^3+3x^2-x-3 &= 0 \\ (-3)^3+3(-3)^2-(-3)-3 &= 0 \\ -27+27+3-3 &= 0 \\ 0 &= 0\,(benar) \end{align}$
Jadi, $x=-3$ adalah akar dari persamaan $x^3+3x^2-x-3=0$.
Catatan:

Jika $x=k$ akar suatu persamaan maka $(x-k)$ merupakan faktor dari persamaan tersebut.

Berdasarkan contoh, persamaan $x^3+3x^2-x-3=0$ akar-akarnya $x=1$, $x=-1$, $x=-3$ maka:
$\begin{align}x^3+3x^2-x-3 &= 0 \\ (x-1)(x+1)(x+3) &= 0 \end{align}$

C. Menentukan Akar-akar Persamaan Suku Banyak

Cara menentukan akar-akar persamaan suku banyak $a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_1x+a_0=0$.

1. Tentukan faktor dari koefisien variabel pangkat tertinggi.
2. Tentukan faktor dari konstanta.
3. Tentukan akar-akar yang mungkin yaitu:
4. Dari akar-akar yang mungkin tersebut, kita substitusi ke persamaan suku banyaknya, jika hasilnya adalah nol maka bilangan tersebut adalah akar pertamanya.
5. Dari akar pertama tersebut, gunakan skema Horner untuk menentukan hasil pembagian.

Contoh 1.
Tentukan akar-akar persamaan $3x^3+x^2-8x+4=0$.
Penyelesaian:
Koefisien variabel pangkat tertinggi: 3
Faktor dari 3 adalah: $\pm 1$, $\pm 3$
Konstanta: 4
Faktor dari 4 adalah: $\pm 1$, $\pm 2$, $\pm 4$
Akar yang mungkin:

Jadi, akar yang mungkin adalah:
$\pm \frac{1}{1}$, $\pm \frac{2}{1}$, $\pm \frac{4}{1}$, $\pm \frac{1}{3}$, $\pm \frac{2}{3}$, $\pm \frac{4}{3}$
$\pm 1$, $\pm 2$, $\pm 4$, $\pm \frac{1}{3}$, $\pm \frac{2}{3}$, $\pm \frac{4}{3}$
Substitusi akar-akar yang mungkin ke persamaan $3x^3+x^2-8x+4=0$.
$x=1$ maka:
$\begin{align}3x^3+x^2-8x+4 &= 0 \\ 3.1^3+1^2-8.1+4 &= 0 \\ 3+1-8+4 &= 0 \\ 0 &= 0\,(benar) \end{align}$
maka $(x-1)$ adalah salah satu faktor dari $3x^3+x^2-8x+4=0$.
Gunakan Pembagian Suku Banyak dengan Skema Horner:
$3x^3+x^2-8x+4=0$ dibagi $(x-1)$

Selanjutnya $3x^2+4x-4$ difaktorkan lagi.
$\begin{align}p\times q &= 3\times (-4) \\ p\times q &= -12 \\ p+q &= 4 \end{align}$

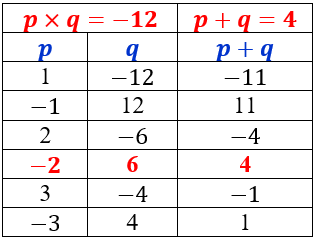
$3x^2+4x-4=\frac{(3x+p)(3x+q)}{3}$
$3x^2+4x-4=\frac{(3x-2)(3x+6)}{3}$
$3x^2+4x-4=(3x-2)(x+2)$
Faktorisasi persamaan suku banyak tersebut adalah:
$\begin{align}3x^3+x^2-8x+4 &= 0 \\ (x-1)(3x^2+4x-4) &= 0 \\ (x-1)(3x-2)(x+2) &= 0 \end{align}$
$x-1=0\to x=1$
$3x-2=0\to x=\frac{2}{3}$
$x+2=0\to x=-2$
Jadi, akar-akar dari persamaan $3x^3+x^2-8x+4=0$ adalah $-2$, 1, dan $\frac{2}{3}$.

---

Contoh 2.
Tentukan akar-akar persamaan $x^3-7x-6=0$.
Penyelesaian:
Koefisien variabel pangkat tertinggi: 1
Faktor dari 1 adalah: $\pm 1$
Konstanta: $-6$
Faktor dari $-6$ adalah: $\pm 1$, $\pm 2$, $\pm 3$, $\pm 6$
Akar yang mungkin:

Jadi, akar yang mungkin adalah:
$\pm \frac{1}{1}$, $\pm \frac{2}{1}$, $\pm \frac{3}{1}$, $\pm \frac{6}{1}$
$\pm 1$, $\pm 2$, $\pm 3$, $\pm 6$
Substitusi akar-akar yang mungkin ke persamaan $x^3-7x-6=0$.
$x=1$ maka:
$\begin{align}x^3-7x-6 &= 0 \\ 1^3-7.1-6 &= 0 \\ 1-7-6 &= 0 \\ -12 &= 0\,(salah) \end{align}$
Jadi, $x=1$ bukan akar dari persamaan $x^3-7x-6=0$. Untuk itu kita selidiki untuk nilai $x$ yang lain.
$x=-1$ maka:
$\begin{align}x^3-7x-6 &= 0 \\ (-1)^3-7(-1)-6 &= 0 \\ -1+7-6 &= 0 \\ 0 &= 0\,(benar) \end{align}$
$x=-1$ akar dari persamaan $x^3-7x-6=0$ maka $(x+1)$ adalah salah satu faktornya.
Gunakan Pembagian Suku Banyak dengan Skema Horner:
$x^3+0x^2-7x-6=0$ dibagi $(x+1)$

Faktorisasi persamaan suku banyak tersebut adalah:
$\begin{align}x^3-7x-6 &= 0 \\ (x+1)(x^2-x-6) &= 0 \\ (x+1)(x-3)(x+2) &= 0 \end{align}$
$x+1=0\to x=-1$
$x-3=0\to x=3$
$x+2=0\to x=-2$
Jadi, akar-akar persamaan $x^3-7x-6=0$ adalah $-2$, $-1$ dan 3.

D. Soal Latihan

Carilah akar-akar dari persamaan suku banyak berikut:
1. $x^3+x^2-10x+8=0$
2. $4x^3-16x^2-x+4=0$
3. $x^3-7x^2+4x+12=0$
4. $x^3+x^2-17x+15=0$

---

Semoga postingan: Polinomial 5. Menentukan Akar-akar Persamaan Suku Banyak ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :