Logaritma 4. Pertidaksamaan Logaritma

Sebelum mempelajari materi pertidaksamaan logaritma, tentu harus lah menguasai materi Persamaan Logaritma.

A. Bentuk-bentuk Pertidaksamaan Logaritma dan Penyelesaiannya

1.	Jika ${^a\log f(x)} \ge {^a\log g(x)}$ dan $a > 1$ maka: Solusi Sementara: HP1:$f(x)\ge g(x)$ Syarat: numerus > 0 HP: $f(x) > 0$ HP3: $g(x) > 0$ HP = $HP1\cap HP2\cap HP3$
2.	Jika ${^a\log f(x)} \le {^a\log g(x)}$ dan $a > 1$ maka: Solusi Sementara: HP1: $f(x)\le g(x)$ Syarat: numerus > 0 HP: $f(x) > 0$ HP3: $g(x) > 0$ HP = $HP1\cap HP2\cap HP3$
3.	Jika ${^a\log f(x)} \ge {^a\log g(x)}$ dan $0 < a < 1$ maka: Solusi Sementara: HP1: $f(x)\le g(x)$ Syarat: numerus > 0 HP: $f(x) > 0$ HP3: $g(x) > 0$ HP = $HP1\cap HP2\cap HP3$
4.	Jika ${^a\log f(x)} \le {^a\log g(x)}$ dan $0 < a < 1$ maka: Solusi Sementara: HP1: $f(x)\ge g(x)$ Syarat: numerus > 0 HP: $f(x) > 0$ HP3: $g(x) > 0$ HP = $HP1\cap HP2\cap HP3$

Contoh 1.

Tentukan himpunan penyelesaian dari pertidaksamaan $^2\log (x-6) > 1$.
Penyelesaian:
$\begin{align}^2\log (x-6) & > 1 \\ ^2\log (x-6) & > {^2\log 2} \\ {^a\log f(x)} & > {^a\log g(x)} \end{align}$
$a=2 > 1$ maka:
Solusi Sementara:
$\begin{align}f(x) & > g(x) \\ x-6 & > 2 \\ x & > 8 \end{align}$
HP1 = $\left\{ x|x > 8 \right\}$
Syarat: numerus > 0
$\begin{align}f(x) & > 0 \\ x-6 & > 0 \\ x & > 6 \end{align}$
HP2 = $\left\{ x|x > 6 \right\}$
Garis bilangan:

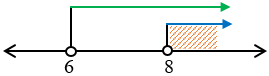
HP = $HP1\cap HP2$
Jadi, HP = $\{x|x > 8\}$

Contoh 2.

Tentukan himpunan penyelesaian dari pertidaksamaan ${^7\log (x^2-5x)} \ge {^7\log (x+7)}$.
Penyelesaian:
$\begin{align}{^7\log (x^2-5x)} & \ge {^7\log (x+7)} \\ {^a\log f(x)} & \ge {^a\log g(x)} \end{align}$
$a=7 > 1$ maka:
Solusi Sementara:
$\begin{align}f(x) & \ge g(x) \\ x^2-5x & \ge x+7 \\ x^2-6x-7 & \ge 0 \\ (x+1)(x-7) & \ge 0 \end{align}$
HP1 = $\left\{ x|x\le -1\,\text{atau}\,x\ge 7 \right\}$
Syarat: numerus > 0
$\begin{align}f(x) & > 0 \\ x^2-5x & > 0 \\ x(x-5) & > 0 \end{align}$
HP2 = $\left\{ x|x < 0\,\text{atau}\,x > 5 \right\}$
$\begin{align}g(x) & > 0 \\ x+7 & > 0 \\ x & > -7 \end{align}$
HP3 = $\left\{ x|x > -7 \right\}$
Garis bilangan:

HP = $HP1\cap HP2\cap HP3$
Jadi, HP = $\{x|-7 < x\le 1\,\text{atau}\,x\ge 7\}$

Contoh 3.

Tentukan himpunan penyelesaian dari pertidaksamaan $^3\log (x^2-16) < 2$.
Penyelesaian:
$\begin{align}^3\log (x^2-16) & < 2 \\ ^3\log (x^2-16) & < {^3\log 3^2} \\ ^3\log (x^2-16) & < {^3\log 9} \\ ^a\log f(x) & < {^a\log g(x)} \end{align}$
$a=3 > 1$ maka:
Solusi Sementara:
$\begin{align}f(x) & < g(x) \\ x^2-16 & < 9 \\ x^2-25 & < 0 \\ (x+5)(x-5) & < 0 \end{align}$
HP1 = $\left\{ x|-5 < x < 5 \right\}$
Syarat: numerus > 0
$\begin{align}f(x) & > 0 \\ x^2-16 & > 0 \\ (x+4)(x-4) & > 0 \end{align}$
HP2 = $\left\{ x|x < -4\,\text{atau}\,x > 4 \right\}$
Garis bilangan:

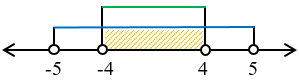
HP = $HP1\cap HP2$
Jadi, HP = {$-5 < x < 5$}

Contoh 4.

Tentukan himpunan penyelesaian dari pertidaksamaan $^5\log (x+5) \le {^5\log (x^2-1)}$.
Penyelesaian:
$\begin{align}^5\log (x+5) & \le {^5\log (x^2-1)} \\ ^a\log f(x) & \le {^a\log g(x)} \end{align}$
$a=5 > 1$ maka:
Solusi Sementara:
$\begin{align}f(x) & \le g(x) \\ x+5 & \le x^2-1 \\ -x^2+x+6 & \le 0 \\ x^2-x-6 &\ge 0 \\ (x+2)(x-3) &\ge 0 \end{align}$
HP1 = $\left\{ x|x\le -2\,\text{atau}\,x\ge 3 \right\}$
Syarat: numerus > 0
$\begin{align}f(x) & > 0 \\ x+5 & > 0 \\ x & > -5 \end{align}$
HP2 = $\left\{ x|x > -5 \right\}$

$\begin{align}g(x) & > 0 \\ x^2-1 & > 0 \\ (x+1)(x-1) & > 0 \end{align}$
HP3 = $\left\{ x|x < -1\,\text{atau}\,x > 1 \right\}$
Garis bilangan:

HP = $HP1\cap HP2\cap HP3$
Jadi, HP = $\left\{ x|x\le -2\,\text{atau}\,x\ge 3 \right\}$

Contoh 5.

Tentukan himpunan penyelesaian dari pertidaksamaan $^{\frac{1}{2}}\log (3x-4) < -2 $.
Penyelesaian:
$\begin{align}^{\frac{1}{2}}\log (3x-4) & < -2 \\ ^{\frac{1}{2}}\log (3x-4) & < {^{\frac{1}{2}}\log \left( \frac{1}{2} \right)^{-2}} \\ ^{\frac{1}{2}}\log (3x-4) & < {^{\frac{1}{2}}\log \left( 2^{-1} \right)^{-2}} \\ ^{\frac{1}{2}}\log (3x-4) & < {^{\frac{1}{2}}\log 4} \\ ^a\log f(x) & < {^a\log g(x)} \end{align}$
$a=\frac{1}{2}$; $0 < a < 1$ maka:
Solusi Sementara:
$\begin{align}f(x) & > g(x) \\ 3x-4 & > 4 \\ 3x & > 8 \\ x > \frac{8}{3} \end{align}$
HP1 = $\left\{ x|x > \frac{8}{3} \right\}$
Syarat: numerus > 0
$\begin{align}f(x) & > 0 \\ 3x-4 & > 0 \\ 3x & > 4 \\ x & > \frac{4}{3} \end{align}$
HP2 = $\left\{ x|x > \frac{4}{3} \right\}$
Garis bilangan:

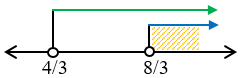
HP = $HP1\cap HP2$
Jadi, HP = $\left\{ x|x>\frac{8}{3} \right\}$

Contoh 6.

Tentukan himpunan penyelesaian dari pertidaksamaan $^{\frac{2}{3}}\log (3x-5) \le {^{\frac{2}{3}}\log (15-2x)}$.
Penyelesaian:
$\begin{align}^{\frac{2}{3}}\log (3x-5) & \le {^{\frac{2}{3}}\log (15-2x)} \\ ^a\log f(x) & \le {^a\log g(x)} \end{align}$
$a=\frac{2}{3}$; $0 < a < 1$ maka:
Solusi Sementara:
$\begin{align}f(x) & \ge g(x) \\ 3x-5 & \ge 15-2x \\ 3x+2x & \ge 15+5 \\ 5x & \ge 20 \\ x & \ge 4 \end{align}$
HP1 = $\left\{ x|x\ge 4 \right\}$
Syarat: numerus > 0
$\begin{align}f(x) & > 0 \\ 3x-5 & > 0 \\ 3x & > 5 \\ x & > \frac{5}{3} \end{align}$
HP2 = $\left\{ x|x > \frac{5}{3} \right\}$
$\begin{align}g(x) & > 0 \\ 15-2x & > 0 \\ -2x & > -15 \\ x & < \frac{15}{2} \end{align}$
HP3 = $\left\{ x|x < \frac{15}{2} \right\}$
Garis bilangan:

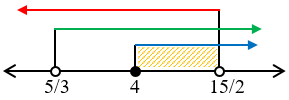
HP = $HP1\cap HP2\cap HP3$
Jadi, HP = $\left\{ x|4 \le x < \frac{15}{2} \right\}$

Contoh 7.

Tentukan himpunan penyelesaian dari pertidaksamaan $^{\frac{3}{5}}\log (x^2+4x+4) > {^{\frac{3}{5}}\log (5x+10)}$.
Penyelesaian:
$\begin{align}^{\frac{3}{5}}\log (x^2+4x+4) & > {^{\frac{3}{5}}\log (5x+10)} \\ ^a\log f(x) & < {^a\log g(x)} \end{align}$
$a=\frac{3}{5}$; $0 < a < 1$ maka:
Solusi Sementara:
$\begin{align}f(x) & < g(x) \\ x^2+4x+4 & < 5x+10 \\ x^2+4x-5x+4-10 & < 0 \\ x^2-x-6 & <0 \\ (x+2)(x-3) & < 0 \end{align}$
HP1 = $\left\{ x|-2 < x < 3 \right\}$
Syarat: numerus > 0
$\begin{align}f(x) & > 0 \\ x^2+4x+4 & > 0 \\ (x+2)(x+2) & > 0 \end{align}$
HP2 = $\left\{ x|x < -2\,\text{atau}\,x > 2 \right\}$ = $\left\{ x|x\ne -2 \right\}$
$\begin{align}g(x) & > 0 \\ 5x+10 & > 0 \\ 5x & > -10 \\ x & > -2 \end{align}$
HP3 = $\left\{ x|x > -2 \right\}$
Garis bilangan:

HP = $HP1\cap HP2\cap HP3$
Jadi, HP = $\left\{ x|-2<x<3 \right\}$

Contoh 8.

Tentukan himpunan penyelesaian dari pertidaksamaan $^3\log x+{^3\log (2x-3)} < 3$.
Penyelesaian:
Solusi Sementara:
$\begin{align}^3\log x+{^3\log (2x-3)} & < 3 \\ ^3\log x(2x-3) & < 3 \\ x(2x-3) & < 3^3 \\ 2x^2-3x-27 & < 0 \\ (2x+3)(x-3) & < 0 \end{align}$
HP1 = $\left\{ x|-\frac{3}{2} < x < 3 \right\}$
Syarat: numerus > 0
$x > 0$
HP2 = $\left\{ x|x > 0 \right\}$
$\begin{align}2x-3 & > 0 \\ 2x & > 3 \\ x & > \frac{3}{2} \end{align}$
HP3 = $\{x|x > \frac{3}{2}\}$
Garis bilangan:

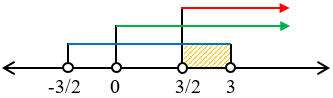
HP = $HP1\cap HP2\cap HP3$
HP = $\left\{ x|\frac{3}{2} < x < 3 \right\}$

Contoh 9.

Tentukan himpunan penyelesaian dari pertidaksamaan $^5\log x-3.{^x\log 5 > 2}$.
Penyelesaian:
Solusi Sementara:
$\begin{align}^5\log x-3.{^x\log 5} & > 2 \\ ^5\log x-\frac{3}{^5\log x} & > 2 \\ \left( ^5\log x \right)^2-3 & > 2.{^5\log x} \\ \left( ^5\log x \right)^2-2.{^5\log x}-3 & > 0 \end{align}$
Misalkan, $^5\log x=p$ maka:
$\begin{align}\left( ^5\log x \right)^2-2.{^5\log x}-3 & > 0 \\ p^2-2p-3 & > 0 \\ (p+1)(p-3) & > 0 \end{align}$
$p < -1 $ atau $p > 3$
$\begin{align}p & < -1 \\ ^5\log x & < -1 \\ x & < 5^{-1} \\ x & < \frac{1}{5} \end{align}$
$\begin{align}p & > 3 \\ ^5\log x & > 3 \\ x & > 5^3 \\ x & > 125 \end{align}$
HP1 = $\left\{ x|x<\frac{1}{5}\,\text{atau}\,x>125 \right\}$
Syarat: numerus > 0
$x>0$
HP2 = $\left\{ x|x >0 \right\}$
Garis bilangan:

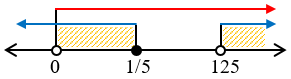
HP = $HP1\cap HP2$
HP = $\left\{ x|0 < x < \frac{1}{5}\,\text{atau}\,x>125 \right\}$

Contoh 10.

Tentukan himpunan penyelesaian dari pertidaksamaan $^{(x-1)}\log (x^2+3x-4) > 2$.
Penyelesaian:
$^{(x-1)}\log (x^2+3x-4) > 2$
Berdasarkan nilai basis yaitu $x-1$ maka ada penyelesaian pertidaksamaan ini kita bagi menjadi 2 kasus yaitu:
Kasus 1. Basis > 1
$\begin{align}x-1 & > 1 \\ x & > 2 \end{align}$
HP1 = $\{x|x > 2\}$
Solusi Sementara:
$\begin{align}^{(x-1)}\log (x^2+3x-4) & > 2 \\ x^2+3x-4 > (x-1)^2 \\ x^2+3x-4 & > x^2-2x+1 \\ x^2-x^2+3x+2x & > 1+4 \\ 5x & > 5 \\ x & > 1 \end{align}$
HP2 = $\{x|x>1\}$
Syarat: numerus > 0
$\begin{align}x^2+3x-4 & > 0 \\ (x+4)(x-1) & > 0 \end{align}$
$x < -4 $ atau $x > 1$
HP3 = $\{x|x < -4\,\text{atau}\,x > 1\}$
Garis bilangan:

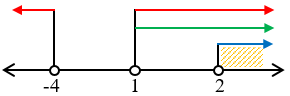
HP = $HP1\cap HP2\cap HP3$
HP = $\{x|x > 2\}$
Kasus 2. 0 < Basis < 1
$0 < x-1 < 1$
$0+1 < x-1+1 < 1+1$
$1 < x < 2$
HP1 = $\{x|1 < x < 2\}$
Solusi Sementara:
$\begin{align}^{(x-1)}\log (x^2+3x-4) & > 2 \\ x^2+3x-4 & < (x-1)^2 \\ x^2+3x-4 & < x^2-2x+1 \\ x^2-x^2+3x+2x & < 1+4 \\ 5x & < 5 \\ x & < 1 \end{align}$
HP2 = $\{x|x < 1\}$
Syarat: numerus > 0
$\begin{align}x^2+3x-4 & > 0 \\ (x+4)(x-1)& > 0 \end{align}$
$x < -4$ atau $x>1$
HP3 = $\{x|x <-4\,\text{atau}\,x>1\}$
Garis bilangan:

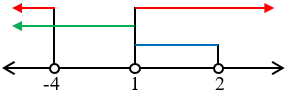
HP = $HP1\cap HP2\cap HP3$
HP = $\{\}$
Dari kasus1 dan kasus 2, diperoleh HP = $\{x|x>2\}$

B. Soal Latihan

1. Tentukan nilai $x$ yang memenuhi pertidaksamaan $^9\log (x^2+2x) < {\frac{1}{2}}$.
2. Tentukan batas-batas nilai $x$ yang memenuhi $\log {(x-1)^2} > {\log (x-1)}$.
3. Tentukan penyelesaian pertidaksamaan $\log (x-4)+\log (x+8) < {\log (2x+16)}$.
4. Tentukan nilai $x$ yang memenuhi pertidaksamaan $2\log x \le \log (2x+5)+2\log 2$.
5. Tentukan himpunan penyelesaian pertidaksamaan $^2\log {(x^2-3x+2)} \ge {^2\log (2-x)}$.

Semoga postingan: Logaritma 4. Pertidaksamaan Logaritma ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :