Statistika 6. Rata-rata Data Berkelompok
Pada pembelajaran kali ini kita akan membahas bagaimana menentukan rataan hitung data berkelompok. Ada beberapa cara menentukan rataan hitung data berkelompok, pada pembelajaran ini yang akan dibahas yaitu:
Langkah-langkah menentukan rataan hitung data berkelompok menggunakan nilai tengah interval.
Contoh:
Diberikan data skor siswa suatu kelas sebagai berikut:

Rataan hitung data tersebut adalah ...
Penyelesaian:

$\bar{x}=\frac{\sum{f_i.x_i}}{\sum{f_i}}=\frac{2950}{40}=73,75$
Jadi, rataan skor siswa adalah 73,75.
Langkah-langkah menentukan rataan hitung data berkelompok menggunakan metode coding atau metode pengkodean.
Contoh:
Diberikan data skor siswa suatu kelas sebagai berikut:
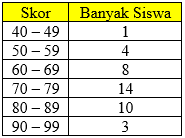
Rataan hitung data tersebut adalah ...
Penyelesaian:
Rataan sementara dipilih dari salah satu nilai tengah kelas. Misalkan, kita pilih dari kelas 70 – 79 maka $\bar{x}_s=\frac{70+79}{2}=74,5$.
Dari kelas 70 – 79 diperoleh:
$t_b$ = 69,5 dan $t_a=79,5$
$c=t_a-t_b=79,5-69,5\Leftrightarrow c=10$

$\begin{align}\bar{x} &= \bar{x}_s+\frac{\sum{f_i.c_i}}{\sum{f_i}}.c \\ &= 74,5+\frac{-3}{40}.10 \\ &= 74,5-0,75 \\ \bar{x} &= 73,75 \end{align}$
Jadi, rataan hitung data tersebut adalah 73,75.

Tentukan:
- Menghitung rata-rata menggunakan nilai tengah.
- Menghitung rata-rata menggunakan metode coding (pengkodean).
A. Rata-rata Data Berkelompok Menggunakan Nilai Tengah Interval
Rumus 1:
$\bar{x}=\frac{\sum{f_i.x_i}}{\sum{f_i}}$; $i$ = 1, 2, 3, ..., n
Keterangan:
$\begin{align}\bar{x} &= \text{rataan hitung} \\ x_i &= \text{nilai tengah kelas ke-i} \\ f_i &= \,\text{frekuensi kelas ke-i} \end{align}$
$\bar{x}=\frac{\sum{f_i.x_i}}{\sum{f_i}}$; $i$ = 1, 2, 3, ..., n
Keterangan:
$\begin{align}\bar{x} &= \text{rataan hitung} \\ x_i &= \text{nilai tengah kelas ke-i} \\ f_i &= \,\text{frekuensi kelas ke-i} \end{align}$
Langkah-langkah menentukan rataan hitung data berkelompok menggunakan nilai tengah interval.
- Tentukan nilai tengah ($x_i$) masing-masing interval dengan rumus: $x_i=\frac{Bb\,+Ba}{2}$ (Bb = Batas bawah kelas dan Ba = Batas atas kelas).
- Tentukan $f_i.x_i$.
- Tentukan $\sum{f_i}$.
- Tentukan $\sum{f_i.x_i}$
- Hitunglah rataan data dengan rumus: $\bar{x}=\frac{\sum{f_i.x_i}}{\sum{f_i}}$.
Contoh:
Diberikan data skor siswa suatu kelas sebagai berikut:

Rataan hitung data tersebut adalah ...
Penyelesaian:

$\bar{x}=\frac{\sum{f_i.x_i}}{\sum{f_i}}=\frac{2950}{40}=73,75$
Jadi, rataan skor siswa adalah 73,75.
B. Rata-rata Data Berkelompok Menggunakan Metode Coding (Pengkodean)
Rumus 2:
$\bar{x}=\bar{x}_s+\frac{\sum{f_i.c_i}}{\sum{f_i}}.c$; $i$ = 1, 2, 3, ..., n
Keterangan:
$\begin{align}\bar{x} &= \text{rataan hitung} \\ x_s &= \text{rataan sementara} \\ c_i &= \text{kode kelas ke-i} \\ f_i &= \,\text{frekuensi kelas ke-i} \\ c &= \text{panjang kelas} \end{align}$
$\bar{x}=\bar{x}_s+\frac{\sum{f_i.c_i}}{\sum{f_i}}.c$; $i$ = 1, 2, 3, ..., n
Keterangan:
$\begin{align}\bar{x} &= \text{rataan hitung} \\ x_s &= \text{rataan sementara} \\ c_i &= \text{kode kelas ke-i} \\ f_i &= \,\text{frekuensi kelas ke-i} \\ c &= \text{panjang kelas} \end{align}$
Langkah-langkah menentukan rataan hitung data berkelompok menggunakan metode coding atau metode pengkodean.
- Tentukan rataan sementara ($\bar{x}_s$). Pada umumnya dipilih nilai tengah pada interval yang berada ditengah.
- Tentukan panjang kelas ($c$) dengan rumus: $c=t_a-t_b$.
- Tentukan kode setiap kelas ($c_i$) dengan rumus: $c_i=\frac{x_i-\bar{x}_s}{c}$
- Tentukan ${f_i.c_i}$.
- Tentukan $\sum{f_i}$
- Tentukan $\sum{f_i.c_i}$
- Hitunglah rataan data dengan rumus: $\bar{x}=\bar{x}_s+\frac{\sum{f_i.c_i}}{\sum{f_i}}.c$.
Contoh:
Diberikan data skor siswa suatu kelas sebagai berikut:

Rataan hitung data tersebut adalah ...
Penyelesaian:
Rataan sementara dipilih dari salah satu nilai tengah kelas. Misalkan, kita pilih dari kelas 70 – 79 maka $\bar{x}_s=\frac{70+79}{2}=74,5$.
Dari kelas 70 – 79 diperoleh:
$t_b$ = 69,5 dan $t_a=79,5$
$c=t_a-t_b=79,5-69,5\Leftrightarrow c=10$

$\begin{align}\bar{x} &= \bar{x}_s+\frac{\sum{f_i.c_i}}{\sum{f_i}}.c \\ &= 74,5+\frac{-3}{40}.10 \\ &= 74,5-0,75 \\ \bar{x} &= 73,75 \end{align}$
Jadi, rataan hitung data tersebut adalah 73,75.
C. Soal Latihan
Data pada tabel berikut menunjukkan tinggi badan peserta seleksi pramugari.
Tentukan:
- Rataan hitung menggunakan nilai tengah kelas.
- Rataan hitung menggunakan metode coding.

Post a Comment for "Statistika 6. Rata-rata Data Berkelompok"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.