Matriks 2. Transpose Matriks, Kesamaan Matriks dan Operasi Aljabar pada Matriks

A. Transpose Matriks

Transpose dari matriks A dilambangkan dengan $A'$, $A^t$ atau $A^T$.
Transpose suatu matriks dapat ditentukan dengan cara:

1. mengubah baris menjadi kolom dan
2. mengubah kolom menjadi baris.

Catatan:
Jika matriks A saama dengan transpose matriks A yaitu$A=A^t$ maka matriks A disebut matriks simetris.
Contoh:
Tentukanlah transpose dari matriks-matriks berikut:
$A = \left( \begin{matrix} 7 & 6 \\ 13 & 2 \\ \end{matrix} \right)$; $B = \left( \begin{matrix} -5 & 6 & 7 \\ 2 & 1 & 8 \\ 3 & 4 & -7 \\ \end{matrix} \right)$; dan $C = \left( \begin{matrix} 6 & 4 & 5 \\ 0 & -2 & -9 \\ \end{matrix} \right)$
Penyelesaian:
$A^t= \left( \begin{matrix} 7 & 13 \\ 6 & 2 \\ \end{matrix} \right)$
$B^t = \left( \begin{matrix} -5 & 2 & 3 \\ 6 & 1 & 4 \\ 7 & 8 & -7 \\ \end{matrix} \right)$
$C^t = \left( \begin{matrix} 6 & 0 \\ 4 & -2 \\ 5 & -9 \\ \end{matrix} \right)$

B. Kesamaan Matriks

Dua matriks dikatakan sama jika ordo kedua matriks sama dan elemen-elemen yang seletak bernilai sama.
Contoh:
Diketahui matriks $A=\left( \begin{matrix} 2x-y & -3 \\ -4 & -8 \\ \end{matrix} \right)$ dan matriks $B = \left( \begin{matrix} -2 & -3 \\ -4 & 3x+y \\ \end{matrix} \right)$. Jika $A=B$ maka nilai dari $2x+y$ adalah ...
Penyelesaian:
$\begin{align}A &= B \\ \left( \begin{matrix} 2x-y & -3 \\ -4 & -8 \\ \end{matrix} \right) &= \left( \begin{matrix} -2 & -3 \\ -4 & 3x+y \\ \end{matrix} \right) \end{align}$
$2x-y=-2$
$3x+y=-8$
-------------- (+)
$\begin{align}5x &= -10 \\ x &= -2 \end{align}$
Substitusi $x=-2$ ke:
$\begin{align}3x+y &= -8 \\ 3(-2)+y &= -8 \\ y &= -2 \end{align}$
maka nilai $2x+y=2(-2)+(-2)=-6$

C. Operasi Aljabar pada Matriks

1. Penjumlahan dan Pengurangan Matriks

Syarat:
Dua matriks atau lebih dapat dijumlahkan atau dikurangkan jika matriks-matriks tersebut memiliki ordo yang sama, dinotasikan dengan:
$A_{m\times n}+B_{m\times n} = C_{m\times n}$
Cara menjumlahkan/mengurangkan dua matriks yaitu jumlahkan atau kurangkan elemen-elemen yang seletak.
Contoh 1.
Diketahui matriks $A = \left( \begin{matrix} 13 & -5 & 6 \\ 7 & -16 & 8 \\ \end{matrix} \right)$ dan $B = \left( \begin{matrix} -20 & -13 & 4 \\ 9 & 5 & -20 \\ \end{matrix} \right)$ maka $A+B$ = ...
Penyelesaian:
A + B
= $\left( \begin{matrix} 13 & -5 & 6 \\ 7 & -16 & 8 \\ \end{matrix} \right)+\left( \begin{matrix} -20 & -13 & 4 \\ 9 & 5 & -20 \\ \end{matrix} \right)$
= $\left( \begin{matrix} 13+(-20) & -5+(-13) & 6+4 \\ 7+9 & -16+5 & 8+(-20) \\ \end{matrix} \right)$ = $\left( \begin{matrix} -17 & -18 & 10 \\ 16 & -11 & -12 \\ \end{matrix} \right)$
Contoh 2.
Diketahui matriks $A = \left( \begin{matrix} 5m+2 & 4 \\ 3n+m & 22 \\ \end{matrix} \right)$; $B = \left( \begin{matrix} 3m+2 & 0 \\ 28 & 14 \\ \end{matrix} \right)$ dan $C = \left( \begin{matrix} 20 & -4 \\ 12 & -8 \\ \end{matrix} \right)$ . Jika $B-A=C$ maka $2m-3n$ = ...
Penyelesaian:

$-2m = 20 \Leftrightarrow m = -10$
$\begin{align}28-3n-m &= 12 \\ -3n-m &= -16 \\ -3n+10 &= -16 \\ -3n &= -26 \\ 3n &= 26 \end{align}$
maka $2m-3n=2(-10)-26=-46$.

2. Perkalian Skalar dengan Suatu Matriks

Suatu matriks dapat dikalikan dengan bilangan real k, dalam hal ini k adalah skalar.
Cara mengalikan bilangan $k\in R$ terhadap suatu matriks adalah dengan mengalikan semua elemen pada matriks tersebut dengan $k$.
Contoh:
Jika matriks $A = \left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)$ maka:
$k.A = k\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right) = \left( \begin{matrix} k.a & k.b \\ k.c & k.d \\ \end{matrix} \right)$

3. Perkalian Matriks dengan Matriks

Syarat:
Dua matriks dapat dikalikan jika banyaknya kolom matriks pertama sama dengan banyaknya baris matriks kedua.
Secara umum dapat dituliskan sebagai berikut:
$A_{m\times n}.B_{n\times p} = C_{m\times p}$
Contoh 1.
Diketahui matriks $A = \left( \begin{matrix} 7 & 5 \\ 4 & 3 \\ \end{matrix} \right)$, $B = \left( \begin{matrix} 2 & -6 \\ -1 & 8 \\ \end{matrix} \right)$ dan $C = \left( \begin{matrix} 2 & -3 & 1 \\ -1 & 0 & 2 \\ \end{matrix} \right)$.
Tentukan hasil perkalian A.B dan B.A, kemudian periksa apakah AB sama dengan BA?
Penyelesaian:

Dari hasil perkalian matriks di atas dapat disimpulkan bahwa pada perkalian matriks $A.B\ne B.A$.

Contoh 2.
Diketahui matriks $P=\left( \begin{matrix} 2 & -3 & 1 \\ -1 & 0 & 2 \\ \end{matrix} \right)$ dan $Q = \left( \begin{matrix} 4 & 6 \\ 5 & 9 \\ 7 & 8 \\ \end{matrix} \right)$ tentukan hasil perkalian dari $P.Q$ dan $Q.P$, kemudian periksa hubungan PQ dengan QP.
Penyelesaian:

Jadi, $P.Q\ne Q.P$

Contoh 3.
Nilai $x$ yang memenuhi persamaan adalah ...
Penyelesaian:

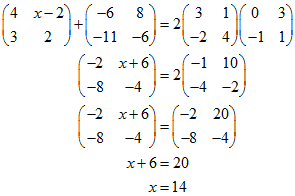
D. Soal Latihan

1. Diketahui matriks $P = \left( \begin{matrix} 4 & -10 \\ 12 & 11 \\ \end{matrix} \right)$ dan $Q = \left( \begin{matrix} 2 & -5 \\ 3 & 6 \\ \end{matrix} \right)$. Tentukanlah $3P-5Q$.
2. Diketahui matriks $M = \left( \begin{matrix} 2 & 7 \\ 4 & -2 \\ -1 & 5 \\ \end{matrix} \right)$. Tentukanlah transpose matriks M.
3. Diketahui matriks $A = \left( \begin{matrix} 6 & 4 \\ -3 & -2 \\ \end{matrix} \right)$, $B = \left( \begin{matrix} -1 & -5 \\ 0 & 3p+1 \\ \end{matrix} \right)$ dan $C = \left( \begin{matrix} 2 & 3 \\ 8 & 5 \\ \end{matrix} \right)$. Jika $3A+2B=C^T$ dimana $C^T$ adalah transpose matriks C, maka nilai $p$ adalah ...
4. Diketahui matriks $A = \left( \begin{matrix} 7 & 9 \\ 8 & 11 \\ \end{matrix} \right)$ dan $B = \left( \begin{matrix} 3 & 4 \\ 2 & 1 \\ \end{matrix} \right)$. Tentukanlah AB dan BA.
5. Nilai $a$ yang memenuhi adalah ...

Semoga postingan: Matriks 2. Transpose Matriks, Kesamaan Matriks dan Operasi Aljabar pada Matriks ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :