Aturan Sinus dan Pembuktiannya

A. Aturan Sinus

Pada segitiga ABC dengan panjang sisi BC = a, panjang sisi AC = b, dan panjang sisi AB = c, maka berlaku:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

Pembuktian Aturan Sinus:
Perhatikan gambar berikut ini!

Perhatikan segitiga BDC:


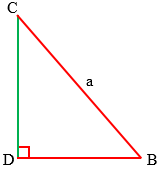
$\begin{align}\sin B &=\frac{CD}{BC} \\ \sin B &=\frac{CD}{a} \\ CD &=a\sin B\,......\,(1) \end{align}$
Perhatikan segitiga ADC:

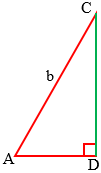
$\begin{align}\sin A &=\frac{CD}{AC} \\ \sin A &=\frac{CD}{b} \\ CD &=b\sin A\,......\,(2) \end{align}$
Dari persamaan (1) dan (2) diperoleh:
$a\sin B=b\sin A\Leftrightarrow \frac{a}{\sin A}=\frac{b}{\sin B}$ ...... (3)
Perhatikan segitiga ABE:

$\begin{align}\sin B &=\frac{AE}{AB} \\ \sin B &=\frac{AE}{c} \\ AE &=c\sin B\,......\,(4) \end{align}$
Perhatikan segitiga AEC:

$\begin{align}\sin C &=\frac{AE}{AC} \\ \sin C &=\frac{AE}{b} \\ AE &=b\sin C\,......\,(5) \end{align}$
Dari persamaan (4) dan (5) diperoleh:
$b\sin C=c\sin B\Leftrightarrow \frac{b}{\sin B}=\frac{c}{\sin C}$ ...... (6)
Dari persamaan (3) dan (6) maka diperoleh:
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$ (terbukti)

B. Contoh Soal dan Pembahasan

Contoh 1.

Diketahui segitiga ABC dengan besar $\angle A=60{}^\circ $, $\angle B=75{}^\circ $, dan panjang AB = 12 cm. Panjang BC adalah ... cm.
Penyelesaian:

$\begin{align}\angle A+\angle B+\angle C &=180^\circ \\ 60^\circ +75^\circ +\angle C &=180^\circ \\ 135^\circ +\angle C &=180^\circ \\ \angle C &=180^\circ -135^\circ \\ \angle C &=45^\circ \end{align}$
Aturan Sinus:
$\begin{align}\frac{a}{\sin A} &=\frac{c}{\sin C} \\ \frac{a}{\sin 60^\circ } &=\frac{12}{\sin 45^\circ } \\ \frac{a}{\cancel{\frac{1}{2}}\sqrt{3}} &=\frac{12}{\cancel{\frac{1}{2}}\sqrt{2}} \\ a &=\frac{12\sqrt{3}}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} \\ a &=\frac{12\sqrt{6}}{2} \\ a &=6\sqrt{6} \end{align}$
Jadi, panjang sisi BC adalah $6\sqrt{6}$ cm.

Contoh 2.

Pada segitiga RST diketahui ST = 4 cm, $\angle R=30^\circ $ dan $\angle T=105^\circ $. Panjang sisi RT adalah ... cm.
Penyelesaian:

$\begin{align}\angle R+\angle S+\angle T &=180^\circ \\ 30^\circ +\angle S+105^\circ &=180^\circ \\ 135^\circ +\angle S &=180^\circ \\ \angle S &=180^\circ -135^\circ \\ \angle S &=45^\circ \end{align}$
Aturan Sinus:
$\begin{align}\frac{s}{\sin S} &=\frac{r}{\sin R} \\ \frac{s}{\sin 45^\circ } &=\frac{4}{\sin 30^\circ } \\ \frac{s}{\cancel{\frac{1}{2}}\sqrt{2}} &=\frac{4}{\cancel{\frac{1}{2}}} \\ s &=4\sqrt{2} \end{align}$
Jadi, panjang sisi RT adalah $4\sqrt{2}$ cm.

Contoh 3.

Ditentukan segitiga ABC dengan panjang sisi BC = 3 cm, sisi AC = 4 cm dan $\sin A=\frac{1}{2}$. Nilai $\cos B$ = ...
Penyelesaian:

Aturan Sinus:
$\begin{align}\frac{\sin B}{b} &=\frac{\sin A}{a} \\ \frac{\sin B}{4} &=\frac{\frac{1}{2}}{3} \\ \sin B &=\frac{2}{3} \end{align}$
Silahkan Baca: Perbandingan Trigonometri
$\sin B=\frac{2}{3}=\frac{de}{mi}$
$\begin{align}sa &=\sqrt{mi^2-de^2} \\ &=\sqrt{3^2-2^2} \\ sa &=\sqrt{5} \end{align}$
$\cos B=\frac{sa}{mi}=\frac{\sqrt{5}}{3}$

Contoh 4.

Perhatikan gambar berikut!

Dua orang mulai berjalan masing-masing dari titik A dan titik B pada saat yang sama. Supaya keduanya sampai di titik C pada saat yang sama, maka kecepatan berjalan dari titik A harus ...
(A) 2 kali kecepatan orang yang dari B.
(B) $\frac{1}{2}\sqrt{2}$ kali kecepatan orang yang dari B.
(C) $\sqrt{2}$ kali kecepatan orang yang dari B.
(D) $2\sqrt{2}$ kali kecepatan orang yang dari B.
(E) $\sqrt{3}$ kali kecepatan orang yang dari B.
Penyelesaian:

Aturan Sinus:
$\frac{a}{\sin A}=\frac{b}{\sin B}\Leftrightarrow \frac{b}{a}=\frac{\sin B}{\sin A}$
a = $s_B$ = jarak tempuh orang dari titik B
b = $s_A$ jarak tempuh orang dari titik A
Ingat: $t=\frac{s}{v}$
$\begin{align}t_A &= t_B \\ \frac{s_A}{v_A} &= \frac{s_B}{v_B} \\ \frac{b}{v_A} &= \frac{a}{v_B} \\ \frac{v_A}{v_B} &= \frac{b}{a} \\ \frac{v_A}{v_B} &= \frac{\sin B}{\sin A} \\ \frac{v_A}{v_B} &= \frac{\sin 30^\circ }{\sin 45^\circ } \\ \frac{v_A}{v_B} &= \frac{\frac{1}{2}}{\frac{1}{2}\sqrt{2}} \\ v_A &= \frac{1}{\sqrt{2}}.v_B \\ v_A &= \frac{1}{2}\sqrt{2}.v_B \end{align}$
Jadi, kecepatan berjalan dari titik A harus $\frac{1}{2}\sqrt{2}$ kali kecepatan orang dari B.
Jawaban: B

Soal Latihan

1. Diketahui segitiga ABC dengan panjang sisi BC = 12 cm, $\angle A=45^\circ $ dan $\angle B=60^\circ $ maka panjang sisi AC = ... cm.
2. Diketahui segitiga PQR dengan panjang sisi PR = 40 cm, $\angle P=62^\circ $ dan $\angle R=79^\circ $ maka panjang sisi QR = .. cm.
3. Diketahui segitiga KLM dengan panjang sisi KM = 8 cm, KL = 6 cm dan $\angle KLM=45^\circ $, maka $\tan \angle KML$ = ....

by: Catatan Matematika

Semoga postingan: Aturan Sinus dan Pembuktiannya ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :