Statistika 10. Ukuran Penyebaran Data Tunggal
A. Jangkauan Data Tunggal (J) atau Rentang Data
Definisi:
Jangkauan Data (J) adalah selisih antara data terbesar ($x_{maks}$) dengan data terkecil ($x_{\min }$).
$J=x_{maks}-x_{\min }$
Jangkauan Data (J) adalah selisih antara data terbesar ($x_{maks}$) dengan data terkecil ($x_{\min }$).
$J=x_{maks}-x_{\min }$
B. Hamparan Data Tunggal (H)
Definisi:
Hamparan (H) adalah selisih antara kuartil ketiga dengan kuartil pertama.
$H=Q_3-Q_1$
Hamparan (H) adalah selisih antara kuartil ketiga dengan kuartil pertama.
$H=Q_3-Q_1$
C. Simpangan Kuartil (${{Q}_{d}}$) Data Tunggal
Definisi:
Simpangan kuartil ($Q_d$) adalah setengah kali panjang hamparan.
$Q_d=\frac{1}{2}H$ atau $Q_d=\frac{1}{2}\left( Q_3-Q_1 \right)$
Contoh 1.Simpangan kuartil ($Q_d$) adalah setengah kali panjang hamparan.
$Q_d=\frac{1}{2}H$ atau $Q_d=\frac{1}{2}\left( Q_3-Q_1 \right)$
Diketahui data: 3, 5, 5, 4, 10, 9, 8, 7, 9. Tentukan jangkauan data, hamparan, dan simpangan kuartil dari data tersebut.
Pembahasan:
$x_{maks}=10$
$x_{\min }=3$
Jangkauan (J):
$\begin{align}
J &=x_{maks}-x_{\min } \\ &=10-3 \\ J &=7 \end{align}$
Data diurutkan menjadi:
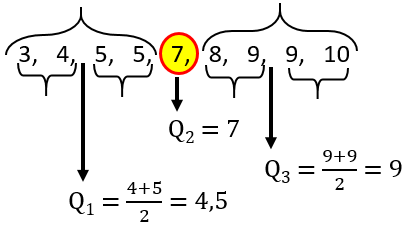
Hamparan (H):
$\begin{align} H &= Q_3 - Q_1 \\ &=9-4,5 \\ H &=4,5 \end{align}$
Simpangan Kuartil ($Q_d$):
$\begin{align} Q_d &= \frac{1}{2}H \\ &= \frac{1}{2}.(4,5) \\ Q_d &= 2,25 \end{align}$
D. Simpangan Rata-rata (SR) Data Tunggal
Definisi:
Simpangan rata-rata menyatakan jarak rata-rata suatu data terhadap rataannya:
$SR=\frac{1}{n}\sum\limits_{i=1}^{n}{|{x_i}-\bar{x}|}$
Keterangan:
SR = Simpangan rata-rata
n = banyaknya data
$x_i$ = nilai data ke-i
$\bar{x}$ = rataan hitung
Contoh 2.Simpangan rata-rata menyatakan jarak rata-rata suatu data terhadap rataannya:
$SR=\frac{1}{n}\sum\limits_{i=1}^{n}{|{x_i}-\bar{x}|}$
Keterangan:
SR = Simpangan rata-rata
n = banyaknya data
$x_i$ = nilai data ke-i
$\bar{x}$ = rataan hitung
Diketahui data: 3, 5, 4, 11, 10, 9, 7. Simpangan rata-rata data tersebut adalah ...
Pembahasan:
$\begin{align} \bar{x} &= \frac{\sum\limits_{i=1}^{n}{{x_i}}}{n} \\ &= \frac{3+5+4+11+10+9+7}{7} \\ &= \frac{49}{7} \\ \bar{x} &= 7 \end{align}$
Simpangan Rata-rata (SR):

E. Ragam/Varians ($S^2$) dan Simpangan Baku (S) Data Tunggal
Definisi:
Ragam menyatakan rata-rata kuadrat jarak suatu data terhadap rataannya.
Ragam/Varians:
$S^2 = \frac{1}{n}\sum\limits_{i=1}^{n}{(x_i-\bar{x})^2}$
Simpangan Baku:
$S=\sqrt{S^2}=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{{(x_i-\bar{x})^2}}}$
Keterangan:
$S^2$ = Ragam (Varians)
S = Simpangan baku
n = banyaknya data
$x_i$ = nilai data ke-i
$\bar{x}$ = rataan hitung
Contoh 3.Ragam menyatakan rata-rata kuadrat jarak suatu data terhadap rataannya.
Ragam/Varians:
$S^2 = \frac{1}{n}\sum\limits_{i=1}^{n}{(x_i-\bar{x})^2}$
Simpangan Baku:
$S=\sqrt{S^2}=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{{(x_i-\bar{x})^2}}}$
Keterangan:
$S^2$ = Ragam (Varians)
S = Simpangan baku
n = banyaknya data
$x_i$ = nilai data ke-i
$\bar{x}$ = rataan hitung
Diketahui data: 4, 5, 3, 7, 9, 8. Ragam dan simpangan baku data tersebut adalah ...
Pembahasan:
$\begin{align} \bar{x} &= \frac{\sum\limits_{i=1}^{n}{x_i}}{n} \\ &= \frac{4+5+3+7+9+8}{6} \\ &= \frac{36}{6} \\ \bar{x} &=6 \end{align}$
Ragam/Varians ($S^2$):
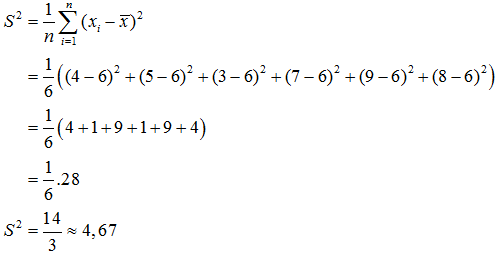
Simpangan Baku (S):
$\begin{align} S &= \sqrt{S^2} \\ &= \sqrt{\frac{14}{3}} \\ &= \frac{\sqrt{14}}{\sqrt{3}} \\ S &= \frac{14}{3}\sqrt{3}\approx 2,16 \end{align}$
F. Soal Latihan
- Simpangan kuartil dari data 6, 7, 7, 3, 8, 4, 6, 5, 5, 9, 10, 10, 4, 4, 3 adalah ...
- Simpangan baku dari data 7, 7, 6, 11, 7, 5, 6, 7 adalah ....
- Diketahui data 7, 10, 12, 15, 16, maka simpangan rata-rata data tersebut adalah ...
- Diberikan sekumpulan data sebagai berikut: 7, 2, 3, 8, 4, 6. Nilai varians data di atas adalah ....
- Suatu data mempunyai rata-rata 35 dan jangkauan 7. Jika setiap nilai dalam data dikali p kemudian dikurangi q di dapat data baru dengan rata-rata 42 dan jangkauan 9. Nilai 7p – q = ...

Pembahasan soal latihan nya mna kak
ReplyDelete