Pembahasan Soal SIMAK UI 2013 Matematika IPA

SIMAK UI 2013. Berikut ini adalah Soal dan Pembahasan Matematika IPA (Saintek) SIMAK UI tahun 2013. Jika adik-adik sekalian ingin membahas soalnya secara mandiri silahkan download (file dalam bentuk pdf), selanjutnya untuk memastikan jawaban kalian sudah benar atau tidak silahkan lihat pembahasan disini.

Matematika IPA SIMAK UI 2013 No. 1

Misalkan $\alpha $ dan $\beta $ merupakan akar-akar persamaan ${{x}^{2}}-bx+6=0$. Jika $\frac{1}{\alpha }$ dan $\frac{1}{\beta }$ adalah akar-akar dari persamaan ${{x}^{2}}-4x+c=0$, maka akar-akar dari persamaan ${{x}^{2}}-(bc)x+bc=0$ merupakan …
A. akar kembar dan positif
B. akar kembar dan negatif
C. dua akar berbeda dan berlainan tanda.
D. dua akar berbeda dan positif.
E. dua akar berbeda dan negatif.
Pembahasan:
${{x}^{2}}-bx+6=0$ akar-akarnya $\alpha $ dan $\beta $
$\alpha +\beta =b$ dan $\alpha .\beta =6$
${{x}^{2}}-4x+c=0$ akar-akarnya $\frac{1}{\alpha }$ dan $\frac{1}{\beta }$
$\frac{1}{\alpha }+\frac{1}{\beta }=4$
$\frac{\alpha +\beta }{\alpha \beta }=4$
$\frac{b}{6}=4\Leftrightarrow b=24$
$\frac{1}{\alpha }.\frac{1}{\beta }=c\Leftrightarrow \frac{1}{\alpha \beta }=c=\frac{1}{6}$
${{x}^{2}}-(bc)x+bc=0$
${{x}^{2}}-\left( 24.\frac{1}{6} \right)x+24.\frac{1}{6}=0$
${{x}^{2}}-4x+4=0$
$(x-2)(x-2)=0$
${{x}_{1}}={{x}_{2}}=2$
Jadi, akar-akarnya kembar dan positif.
Jawaban: A

Matematika IPA SIMAK UI 2013 No. 2

Jika $P'(x)$ menyatakan turunan dari suku banyak $P(x)$ terhadap $x$, sisa pembagian $P(x)$ oleh ${{(x-a)}^{2}}$ adalah …
A. $P'(a)(x-a)+P(a)$
B. $2P'(a)(x-a)+P(a)$
C. $P'(a)P(a)(x-a)+P(a)$
D. $P'(a){{(x-a)}^{2}}$
E. $P'(a){{(x-a)}^{2}}+P(a)$
Pembahasan:
Misal hasil pembagian = H(x) dan sisa pembagian $(mx+n)$
Yang dibagi = pembagi x hasil + sisa
$P(x)={{(x-a)}^{2}}.H(x)+(mx+n)$
$P(a)={{(a-a)}^{2}}.H(a)+(m.a+n)$
$P(a)=m.a+n$ ….. pers (1)
$P'(x)=2(x-a).H(x)+{{(x-a)}^{2}}.H'(x)+m$
$P'(a)=2(a-a).H(a)+{{(a-a)}^{2}}.H'(a)+m$
$P'(a)=m$ substitusi ke pers (1):
$P(a)=m.a+n$
$P(a)=P'(a).a+n\Leftrightarrow n=P(a)-aP'(a)$
Jadi, sisa pembagian:
= $(mx+n)$
= $P'(a)x+P(a)-aP'(a)$
= $P'(a)(x-a)+P(a)$
Jawaban: A

Matematika IPA SIMAK UI 2013 No. 3

Jika ${{x}^{4}}+4{{x}^{3}}+(2p+2){{x}^{2}}+(2p+5q+2)x+(3q+2r)$ habis dibagi oleh ${{x}^{3}}+2{{x}^{2}}+8x+6$, nilai $(p-q)r$ adalah …
A. -21
B. -9
C. 9
D. 10
E. 21
Pembahasan:
Pembagian bersusun panjang:
${{x}^{4}}+4{{x}^{3}}+(2p+2){{x}^{2}}+(2p+5q+2)x+(3q+2r)$
= $({{x}^{3}}+2{{x}^{2}}+8x+6)(x+2)$
= ${{x}^{4}}+4{{x}^{3}}+12{{x}^{2}}+22x+12$
Perhatikan koefisiennya:
Koefisien $x^2$ adalah:
$\begin{align} 2p+2 &= 12 \\ 2p &= 10 \\ p &= 5 \end{align}$
Koefisien $x$ adalah:
$\begin{align} 2p+5q+2 &= 22 \\ 2.5+5q+2 &= 22 \\ 5q+12 &= 22 \\ 5q &= 10 \\ q &= 2 \end{align}$
Konstanta:
$\begin{align} 3q+2r &= 12 \\ 3.2+2r &= 12 \\ 2r &= 6 \\ r &= 3 \end{align}$
$(p-q)r=(5-2).3=9$
Jawaban: C

Matematika IPA SIMAK UI 2013 No. 4

Diketahui dua sistem persamaan linier berikut mempunyai solusi yang sama:
$\left\{ \begin{array}{*{35}{l}} ax+2y=b+1 \\ x+y=3 \\ \end{array} \right.$ dan $\left\{ \begin{array}{*{35}{l}} 2x+y={{a}^{2}}+2 \\ x+3y=3 \\ \end{array} \right.$
Maka nilai $a-b$ adalah …
A. -9
B. -5
C. 0
D. 5
E. 9
Pembahasan:
$ax+2y=b+1$ …. (1)
$x+y=3$ … (2)
$2x+y={{a}^{2}}+2$ …. (3)
$x+3y=3$ …. (4)
Pers (4) dikurang pers (2):
$x+3y=3$
$x+y=3$
----------- (-)
$2y=0\Leftrightarrow y=0\,dan\,x=3$
Substitusi ke (3):
$2x+y={{a}^{2}}+2$
$2.3+0={{a}^{2}}+2\Leftrightarrow a=\pm 2$
Pers (1):
$ax+2y=b+1$
$3a+2.0=b+1\Leftrightarrow b=3a-1$
$a=2\to b=3.2-1=5\to a-b=-3$
$a=-2\to b=3(-2)-1=-7\to a-b=5$
Jawaban: D

Matematika IPA SIMAK UI 2013 No. 5

Diketahui ${{a}^{2}}-{{b}^{2}}+{{c}^{2}}-{{d}^{2}}=2010$ dan $a+b+c+d=2010$. Jika $a$, $b$, $c$, $d$ adalah empat suku pertama dari suatu barisan aritmetika, maka $a$ = …
A. 1008
B. 898
C. 788
D. 604
E. 504
Pembahasan:
Barisan Aritmetika: $a$, $b$, $c$, $d$ maka:
$a-b=c-d$
${{a}^{2}}-{{b}^{2}}+{{c}^{2}}-{{d}^{2}}=2010$
$(a-b)(a+b)+(c-d)(c+d)=2010$
$(a-b)(a+b)+(a-b)(c+d)=2010$
$(a-b)(a+b+c+d)=2010$
$(a-b).2010=2010$
$a-b=1\to b-a=-1$
Barisan Aritmetika:
$beda=b-a=-1$
$a+b+c+d=2010$
$a+(a-1)+(a-2)+(a-3)=2010$
$4a=2016\Leftrightarrow a=504$
Jawaban: E

Matematika IPA SIMAK UI 2013 No. 6

Fungsi $f(x)$ dan $g(x)$ dengan $f(0)g(0)=0$ memenuhi persamaan matriks berikut:
$\left( \begin{matrix} f(x) & g(x) \\ 1 & -1 \\ \end{matrix} \right)\left( \begin{matrix} g'(x) & 0 \\ f'(x) & 0 \\ \end{matrix} \right)=\left( \begin{matrix} 4{{x}^{3}}-8x & 0 \\ 4 & 0 \\ \end{matrix} \right)$
Nilai dari $f(4)$ adalah …
A. 24
B. 20
C. 16
D. 12
E. 8
Pembahasan:
$\left( \begin{matrix} f(x) & g(x) \\ 1 & -1 \\ \end{matrix} \right)\left( \begin{matrix} g'(x) & 0 \\ f'(x) & 0 \\ \end{matrix} \right)=\left( \begin{matrix} 4{{x}^{3}}-8x & 0 \\ 4 & 0 \\ \end{matrix} \right)$
$\left( \begin{matrix}f(x).g'(x)+g(x).f'(x) & 0 \\g'(x)-f'(x) & 0 \\ \end{matrix} \right)=\left( \begin{matrix} 4{{x}^{3}}-8x & 0 \\ 4 & 0 \\ \end{matrix} \right)$
1) $f(x).g'(x)+g(x).f'(x)=4{{x}^{3}}-8x$
$\int{\left( f(x).g'(x)+g(x).f'(x) \right)}dx=\int{\left( 4{{x}^{3}}-8x \right)}dx$
$f(x).g(x)={{x}^{4}}-4{{x}^{2}}+c$
$f(0).g(0)={{0}^{4}}-{{4.0}^{2}}+c=0\Leftrightarrow c=0$
2) $g'(x)-f'(x)=4$
$\int{\left( g'(x)-f'(x) \right)dx}=\int{4dx}$
$g(x)-f(x)=4x+c$
$g(x)-f(x)=4x$
$f(x).g(x)={{x}^{4}}-4{{x}^{2}}$
$f(x).g(x)=({{x}^{2}}-2x)({{x}^{2}}+2x)$
$f(x)={{x}^{2}}-2x$
$f(4)={{4}^{2}}-2.4=8$
Jawaban: E

Matematika IPA SIMAK UI 2013 No. 7

Himpunan penyelesaian dari pertidaksamaan $\log ({{5}^{2x}}+25) > x(1-\log 2)+\log 2+\log 13$ adalah …
A. $\left\{ x\in R|x < 0\,atau\,x > 2 \right\}$
B. $\left\{ x\in R|0 < x < 2 \right\}$
C. $\left\{ x\in R|x \le 0\,atau\,x \ge 2 \right\}$
D. $\left\{ x\in R|0 \le x < 2 \right\}$
E. $\left\{ x\in R|x > 2 \right\}$
Pembahasan:
$\log ({{5}^{2x}}+25) > x(1-\log 2)+\log 2+\log 13$
$\log ({{5}^{2x}}+25) > x(\log 10-\log 2)+\log (2.13)$
$\log ({{5}^{2x}}+25) > x.\log 5+\log 26$
$\log ({{5}^{2x}}+25) > \log ({{5}^{x}}.26)$
${{5}^{2x}}+25 > {{26.5}^{x}}$
${{({{5}^{x}})}^{2}}-{{26.5}^{x}}+25 > 0$
$({{5}^{x}}-1)({{5}^{x}}-25) > 0$
${{5}^{x}} < 1$ atau ${{5}^{x}} > 25$
${{5}^{x}} < {{5}^{0}}$ atau ${{5}^{x}} > {{5}^{2}}$
$x < 0$ atau $x > 2$
Jawaban: A

Matematika IPA SIMAK UI 2013 No. 8

Nilai dari $\csc {{10}^{o}}-\sqrt{3}\sec {{10}^{o}}$ adalah …
A. -4
B. -2
C. 0
D. 2
E. 4
Pembahasan:
$\csc {{10}^{o}}-\sqrt{3}\sec {{10}^{o}}$
= $\frac{1}{\sin {{10}^{o}}}-\frac{\sqrt{3}}{\cos {{10}^{o}}}$
= $2\left( \frac{\frac{1}{2}}{\sin {{10}^{o}}}-\frac{\frac{1}{2}\sqrt{3}}{\cos {{10}^{o}}} \right)$
= $2\left( \frac{\cos {{60}^{o}}}{\sin {{10}^{o}}}-\frac{\sin {{60}^{o}}}{\cos {{10}^{o}}} \right)$
= $2\left( \frac{\cos {{60}^{o}}.\cos {{10}^{o}}-\sin {{60}^{o}}.\sin {{10}^{o}}}{\sin {{10}^{o}}.\cos {{10}^{o}}} \right)$
= $2.\frac{\cos {{70}^{o}}}{\frac{1}{2}.\sin {{20}^{o}}}$
= $\frac{4.\cos {{70}^{o}}}{\sin ({{90}^{o}}-{{70}^{o}})}$
= $\frac{4.\cos {{70}^{o}}}{\cos {{70}^{o}}}=4$
Jawaban: E

Matematika IPA SIMAK UI 2013 No. 9

Diketahui bahwa $\underset{x\to 5}{\mathop{\lim }}\,\frac{f(x)g(x)-3g(x)+f(x)-3}{(f(x)-3)(x-5)}$ terdefinisi. Nilai dari $g(5)$ = …
A. 3
B. 2
C. 1
D. 0
E. -1
Pembahasan:
$\underset{x\to 5}{\mathop{\lim }}\,\frac{f(x)g(x)-3g(x)+f(x)-3}{(f(x)-3)(x-5)}$
= $\underset{x\to 5}{\mathop{\lim }}\,\frac{\left( f(x)-3 \right)g(x)+f(x)-3}{(f(x)-3)(x-5)}$
= $\underset{x\to 5}{\mathop{\lim }}\,\frac{\left( f(x)-3 \right).\left( g(x)+1 \right)}{(f(x)-3)(x-5)}$
= $\underset{x\to 5}{\mathop{\lim }}\,\frac{g(x)+1}{(x-5)}=\frac{0}{0}$
$g(5)+1=0\Leftrightarrow g(5)=-1$
Jawaban: E

Matematika IPA SIMAK UI 2013 No. 10

Nilai dari $\int\limits_{-\frac{\pi }{4}}^{\frac{\pi }{4}}{\left( \sin x+{{\sin }^{3}}x+{{\sin }^{5}}x+... \right)}dx$ adalah …
A. $-2\sqrt{2}$
B. $-\sqrt{2}$
C. 0
D. $\frac{1}{2}\sqrt{2}$
E. $2\sqrt{2}$
Pembahasan:
$\sin x+{{\sin }^{3}}x+{{\sin }^{5}}x+...={{S}_{\infty }}$
$a=\sin x$ dan $r={{\sin }^{2}}x$
${{S}_{\infty }}=\frac{a}{1-r}$
${{S}_{\infty }}=\frac{\sin x}{1-{{\sin }^{2}}x}=\frac{\sin x}{{{\cos }^{2}}x}=\tan x.\sec x$
$\int\limits_{-\frac{\pi }{4}}^{\frac{\pi }{4}}{\left( \sin x+{{\sin }^{3}}x+{{\sin }^{5}}x+... \right)}dx$
= $\int\limits_{-\frac{\pi }{4}}^{\frac{\pi }{4}}{\tan x.\sec x\,}dx$
= $\left. \sec x \right|_{-\frac{\pi }{4}}^{\frac{\pi }{4}}$
= $\sec \left( \frac{\pi }{4} \right)-\sec \left( -\frac{\pi }{4} \right)$
= $\sqrt{2}-\sqrt{2}=0$
Jawaban: C

Matematika IPA SIMAK UI 2013 No. 11

Pada kubus ABCD.EFGH, titik P terletak pada segmen BG sehingga $PG=2\times BP$. Titik Q adalah titik potong garis HP dan bidang ABCD. Jika panjang sisi kubus 6 cm, luas segitiga APQ adalah … $c{{m}^{2}}$.
A. $18\sqrt{2}$
B. $9\sqrt{2}$
C. $3\sqrt{2}$
D. 4
E. 2
Pembahasan:
$PG=2\times BP$
Perhatikan gambar berikut!

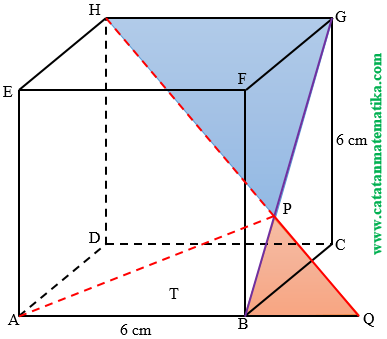
$\Delta HGP$ sebangun dengan $\Delta QBP$ maka:
$\frac{PG}{BP}=\frac{HG}{BQ}$
$\frac{2\times BP}{BP}=\frac{6}{BQ}$
$2\times BQ=6\Leftrightarrow BQ=3$
$AQ=AB+BQ=6+3=9$
$PG=2\times BP$ tambahkan BP
$PG+BP=2\times BP+BP$
$6\sqrt{2}=3\times BP\Leftrightarrow BP=2\sqrt{2}$
$\begin{align} {{L}_{APQ}} &= \frac{1}{2}.AQ.BP \\ &= \frac{1}{2}.9.2\sqrt{2} \\ &= 9\sqrt{2} \end{align}$
Jawaban: B

Matematika IPA SIMAK UI 2013 No. 12

Untuk $-\frac{3\pi }{2} < x < 2\pi $, banyaknya nilai $x$ yang memenuhi persamaan ${{\left( \sin 2x+\sqrt{3}\cos 2x \right)}^{2}}-5$ = $\cos \left( \frac{\pi }{6}-2x \right)$ adalah …
A. 4
B. 3
C. 2
D. 1
E. 0
Pembahasan:
Teori:
$A\cos 2x+B\sin x=\sqrt{{{A}^{2}}+{{B}^{2}}}.\cos (x-a)$
$\tan \alpha =\frac{B}{A}$
$\sin 2x+\sqrt{3}\cos 2x=\sqrt{3}\cos 2x+\sin 2x=?$ $A=\sqrt{3}$, $B=1$
$\tan \alpha =\frac{1}{\sqrt{3}}\to \alpha =\frac{\pi }{6}$
${{\left( \sin 2x+\sqrt{3}\cos 2x \right)}^{2}}-5$ = $\cos \left( \frac{\pi }{6}-2x \right)$
${{\left( \sqrt{3}\cos 2x+\sin 2x \right)}^{2}}-5$ = $\cos -\left( 2x-\frac{\pi }{6} \right)$
${{\left( \sqrt{{{(\sqrt{3})}^{2}}+{{1}^{2}}}.cos\left( 2x-\frac{\pi }{6} \right) \right)}^{2}}-5$ = $\cos \left( 2x-\frac{\pi }{6} \right)$
$4co{{s}^{2}}\left( 2x-\frac{\pi }{6} \right)-\cos \left( 2x-\frac{\pi }{6} \right)-5=0$
$\left( 4cos\left( 2x-\frac{\pi }{6} \right)-5 \right)\left( \cos \left( 2x-\frac{\pi }{6} \right)+1 \right)=0$
$cos\left( 2x-\frac{\pi }{6} \right)=\frac{5}{4}$ (Tidak memenuhi)
$cos\left( 2x-\frac{\pi }{6} \right)=-1$
$cos\left( 2x-\frac{\pi }{6} \right)=\cos \pi $ 1) $2x-\frac{\pi }{6}=\pi +2k\pi $
$k=0\to x=\frac{7}{12}\pi $ dan $k=1\to x=\frac{19}{12}\pi $ 2) $2x-\frac{\pi }{6}=-\pi +2k\pi $
$k=0\to x=-\frac{5}{12}\pi $ dan $k=-1\to x=-\frac{17}{12}\pi $
Jadi, banyaknya nilai $x$ yang memenuhi ada 4.
Jawaban: A

---

Baca juga:

Download Kumpulan Soal SIMAK UI Lengkap. Soal dan Pembahasan Matematika Dasar SIMAK UI 2013. Soal dan Pembahasan Matematika Dasar SIMAK UI 2012. Soal dan Pembahasan Matematika IPA SIMAK UI 2012. Soal dan Pembahasan Matematika Dasar SIMAK UI 2011. Soal dan Pembahasan Matematika IPA SIMAK UI 2011.

Semoga postingan: Pembahasan Soal SIMAK UI 2013 Matematika IPA ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :