Pembahasan Soal SIMAK UI 2013 Matematika Dasar
Berikut ini adalah Soal dan Pembahasan Matematika Dasar SIMAK UI Tahun 2013 dengan kode soal 333. Jika kalian ingin download soalnya aja terlebih dahulu, silahkan. Dan jangan sungkan untuk share/bagikan ke teman-teman atau siswanya ya...!
Download Soal Matematika Dasar SIMAK UI 2013 Kode 333
Matematika Dasar SIMAK UI 2013 No. 1
Dari 26 huruf alphabet dipilih satu per satu 8 huruf sembarang dengan cara pengembalian dan disusun sehingga membentuk kata. Probabilitas bahwa di antara kata-kata yang terbentuk mengandung subkata “SIMAKUI” dalam satu rangkaian kata yang tidak terpisah adalah ….
A. $\frac{26}{{{26}^{8}}}$ B. $\frac{52}{{{26}^{8}}}$ C. $\frac{26}{\left( \begin{matrix} 26 \\ 8 \\ \end{matrix} \right)}$ D. $\frac{52}{\left( \begin{matrix} 26 \\ 8 \\ \end{matrix} \right)}$ E. $\frac{1}{8}$
Pembahasan:
n(A) = banyak susunan 8 huruf yang didalamnya mengandung subkat “SIMAKUI”. Kemungkinannya ada 2 yaitu:
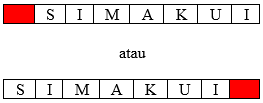
Kotak merah diisikan salah satu huruf dari 26 huruf alphabet, maka diperoleh:
n(A) = 2 x 26 = 52
n(S) = banyak susunan 8 huruf sembarang dari 26 huruf = ${{26}^{8}}$.
$P(A)=\frac{n(A)}{n(S)}=\frac{52}{{{26}^{8}}}$
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 2
Jika ${}^{2}\log {{(}^{3}}\log {{(}^{4}}\log x))$ = $^{3}\log {{(}^{4}}\log {{(}^{2}}\log y))$ = $^{4}\log {{(}^{2}}\log {{(}^{3}}\log z))$ = 0, Nilai dari $x+y+z$ = …
A. 50 B. 58 C. 89 D. 111 E. 1296
Pembahasan:
*)
${}^{2}\log {{(}^{3}}\log {{(}^{4}}\log x))=0$
$^{3}\log {{(}^{4}}\log x)={{2}^{0}}$
$^{3}\log {{(}^{4}}\log x)=1$
$^{4}\log x={{3}^{1}}$
$x={{4}^{3}}=64$
*)
$^{3}\log {{(}^{4}}\log {{(}^{2}}\log y))=0$
$^{4}\log {{(}^{2}}\log y)={{3}^{0}}$
$^{4}\log {{(}^{2}}\log y)=1$
$^{2}\log y={{4}^{1}}$
$y={{2}^{4}}=16$
*)
$^{4}\log {{(}^{2}}\log {{(}^{3}}\log z))=0$
$^{2}\log {{(}^{3}}\log z)={{4}^{0}}$
$^{2}\log {{(}^{3}}\log z)=1$
$^{3}\log z={{2}^{1}}$
$z={{3}^{2}}=9$
*) maka $x+y+z=64+16+9=89$.
Jawaban: C
Matematika Dasar SIMAK UI 2013 No. 3
Diketahui bahwa $f(x)=mz+n$ dan $g(z)=pz+q$ untuk $m,n,p,q\in R$. Dengan demikian, $f(g(x))=g(f(x))$ akan memiliki solusi untuk …
A. jika dan hanya jika $n(1-p)-q(1-m)=0$.
B. jika dan hanya jika $(1-n)(1-p)-(1-q)(1-m)=0$
C. jika dan hanya jika $m=p$ dan $n=q$.
D. jika dan hanya jika $mq-np=0$
E. setiap pilihan $m,n,p,q$.
Pembahasan:
$f(g(x))=g(f(x))$
$f(px+q)=g(mx+n)$
$m(px+q)+n=p(mx+n)+q$
$mpx+mq+n=pmx+pn+q$
$mq+n=pn+q$
$n-pn=q-mq$
$n(1-p)=(1-m)q$
$n(1-p)-(1-m)q=0$
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 4
Jika r dan s adalah akar-akar persamaan $a{{x}^{2}}+bx+c=0$ dan D adalah diskriminan dari persamaan tersebut, nilai dari $\frac{1}{{{r}^{2}}}+\frac{1}{{{s}^{2}}}$ adalah …
A. $\frac{D}{{{c}^{2}}}+\frac{2a}{c}$
B. $\frac{D}{2a}+c$
C. $\frac{D}{{{c}^{2}}}$
D. $\frac{D}{2a}$
E. $D$
Pembahasan:
$a{{x}^{2}}+bx+c=0$, akar-akarnya r dan s, maka:
$r+s=\frac{-b}{a}$ dan $r.s=\frac{c}{a}$
$D={{b}^{2}}-4ac$
$\frac{1}{{{r}^{2}}}+\frac{1}{{{s}^{2}}}=\frac{{{r}^{2}}+{{s}^{2}}}{{{r}^{2}}{{s}^{2}}}$
$=\frac{{{(r+s)}^{2}}-2rs}{{{(rs)}^{2}}}$
$=\frac{{{\left( \frac{-b}{a} \right)}^{2}}-2.\frac{c}{a}}{{{\left( \frac{c}{a} \right)}^{2}}}$
$=\frac{\frac{{{b}^{2}}}{{{a}^{2}}}-\frac{2c}{a}}{\frac{{{c}^{2}}}{{{a}^{2}}}}$
$=\frac{{{b}^{2}}-2ac}{{{a}^{2}}}\times \frac{{{a}^{2}}}{{{c}^{2}}}$
$=\frac{{{b}^{2}}-2ac}{{{c}^{2}}}$
$=\frac{{{b}^{2}}-4ac}{{{c}^{2}}}+\frac{2ac}{{{c}^{2}}}$
$=\frac{D}{{{c}^{2}}}+\frac{2a}{c}$
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 5
Jika diketahui bahwa $x=\frac{1}{2013}-\frac{2}{2013}+\frac{3}{2013}-\frac{4}{2013}+...-\frac{2012}{2013}$, nilai $x$ yang memenuhi adalah …
A. $-\frac{1007}{2013}$
B. $-\frac{1006}{2013}$
C. $\frac{1}{2013}$
D. $\frac{1006}{2013}$
E. $\frac{1007}{2013}$
Pembahasan:
$1-2+3-4+...+2011-2012$
$=(1-2)+(3-4)+...+(2011-2012)$
$=(-1)+(-1)+...+(-1)$ {sebanyak 1006}
Maka:
$1-2+3-4+...-2012=(-1).1006=-1006$
$x=\frac{1}{2013}-\frac{2}{2013}+\frac{3}{2013}-\frac{4}{2013}+...-\frac{2012}{2013}$
$x=\frac{1-2+3-4+...-2012}{2013}$
$x=\frac{-1006}{2013}$
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 6
Diketahui bahwa ${{2}^{w}}.{{a}^{x}}.{{b}^{y}}.{{c}^{z}}=2013$ untuk setiap a, b, c, d, x, y, z merupakan bilangan bulat positif dan w bilangan bulat nonnegative dengan $a < b < c$. Nilai $2w+ax+by+cz$ = …
A. 0 B. 3 C. 11 D. 75 E. 611
Pembahasan:
${{2}^{w}}.{{a}^{x}}.{{b}^{y}}.{{c}^{z}}=2013$
Factor dari 2013 adalah 3, 11, dan 61 sehingga:
${{2}^{0}}{{.3}^{1}}{{.11}^{1}}{{.61}^{1}}=2013$
${{2}^{0}}{{.3}^{1}}{{.11}^{1}}{{.61}^{1}}={{2}^{w}}.{{a}^{x}}.{{b}^{y}}.{{c}^{z}}$
$w=0$, $a=3$, $x=1$, $b=11$, $y=1$, $c=61$, $z=1$
$2w+ax+by+cz=2.0+3.1+11.1+61.1=75$
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 7
Perhatikan gambar berikut ini.
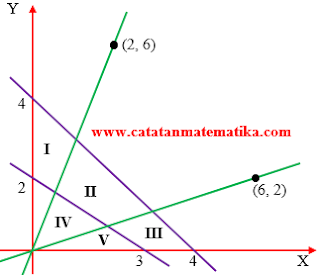
Himpunan penyelesaian system pertidaksamaan , , , adalah …
A. I B. II C. III D. IV E. V
Pembahasan:
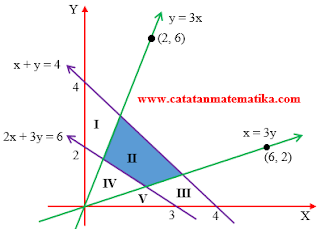
Maka daerah penyelesaiannya adalah II.
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 8
Bilangan bulat terbesar $a$ sehingga hanya terdapat tiga pasangan bilangan bulat $(x,y)$ yang memenuhi system pertidaksamaan berikut:
$\left\{ \begin{matrix} 3y-x < 5 \\ y+ax < 11 \\ 4y+x > 9 \\ \end{matrix} \right.$
adalah …
A. -1 B. 0 C. 1 D. 2 E. 3
Pembahasan:

Tiga pasangan (x,y) bilangan bulat yang memenuhi sistem yaitu:
$(2,2)$, $(3,2)$, $(4,2)$
Substitusi ke: $y+ax < 11$
$(2,2)\to 2+2a < 11 \Leftrightarrow a < \frac{9}{2}=\{...,1,2,3,4\}$
$(3,2)\to 2+3a < 11 \Leftrightarrow a < 3=\{...,1,2\}$
$(4,2)\to 2+4a < 11 \Leftrightarrow a < \frac{9}{4}=\{...,1,2\}$
Sehingga nilai a terbesar adalah 2.
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 9
Jika $A=\left[ \begin{matrix} 4 & 3 \\ 2 & 5 \\ \end{matrix} \right]$ dan ${{A}^{2}}-xA+yI=\left[ \begin{matrix} 0 & 0 \\ 0 & 0 \\ \end{matrix} \right]$ maka $x+y$ = …
A. 9 B. 14 C. 19 D. 23 E. 25
Pembahasan:
${{A}^{2}}-xA+yI=\left[ \begin{matrix} 0 & 0 \\ 0 & 0 \\ \end{matrix} \right]$
${{A}^{2}}-xA+yI=0$
${{A}^{2}}=xA-yI$
${{\left[ \begin{matrix} 4 & 3 \\ 2 & 5 \\ \end{matrix} \right]}^{2}}=x\left[ \begin{matrix} 4 & 3 \\ 2 & 5 \\ \end{matrix} \right]-y\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right]$
$\left[ \begin{matrix} 22 & 27 \\ 18 & 31 \\ \end{matrix} \right]=\left[ \begin{matrix} 4x & 3x \\ 2x & 5x \\ \end{matrix} \right]-\left[ \begin{matrix} y & 0 \\ 0 & y \\ \end{matrix} \right]$
$\left[ \begin{matrix} 22 & 27 \\ 18 & 31 \\ \end{matrix} \right]=\left[ \begin{matrix} 4x-y & 3x \\ 2x & 5x-y \\ \end{matrix} \right]$
$3x=27\to x=9$
$4x-y=22\Leftrightarrow 4.9-y=22\Leftrightarrow y=14$
$x+y=9+14=23$
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 10
Diketahui bilangan $a,b,c$ membentuk barisan geometri. Bilangan $a,b,c-2$ membentuk barisan aritmetika dan bilangan $a,b+2,c+10$ membentuk barisan geometri. Jumlah semua nilai yang mungkin untuk $b$ adalah …
A. $\frac{14}{9}$ B. $\frac{20}{9}$ C. $\frac{32}{9}$ D. $\frac{40}{9}$ E. $\frac{80}{9}$
Pembahasan:
Barisan Geometri:
$a,b,c\Rightarrow {{b}^{2}}=ac$ …. (1)
Barisan Aritmetika:
$a,b,c-2\Rightarrow 2b=a+c-2$ …. (2)
Barisan Geometri:
$a,b+2,c+10$ maka:
${{(b+2)}^{2}}=a(c+10)$
${{b}^{2}}+4b+4=ac+10a$
${{b}^{2}}+4b+4={{b}^{2}}+10a$
$4b+4=10a$
$2b+2=5a$ …. (3)
Substitusi (2) ke (3), diperoleh:
$a+c-2+2=5a$
$c=4a$ substitusi ke (1)
${{b}^{2}}=ac\Leftrightarrow {{b}^{2}}=a.4a\Leftrightarrow b=\pm 2a$
Substitusi ke persamaan (3)
Untuk $b=2a$ maka:
$2b+2=5a$
$2.2a+2=5a$
$4a+2=5a$
$a=2$
$b=2a\to {{b}_{1}}=2.2=4$
Untuk $b=-2a$ maka:
$2b+2=5a$
$2(-2a)+2=5a$
$-4a+2=5a$
$a=\frac{2}{9}$
$b=-2a\to {{b}_{2}}=-2.\frac{2}{9}=-\frac{4}{9}$
${{b}_{1}}+{{b}_{2}}=4-\frac{4}{9}=\frac{32}{9}$
Jawaban: C
Matematika Dasar SIMAK UI 2013 No. 11
$\underset{x\to 5}{\mathop{\lim }}\,\frac{\sqrt{x+2\sqrt{x+1}}}{\sqrt{x-2\sqrt{x+1}}}=...$
A. $\sqrt{3}+\sqrt{2}$
B. $5-2\sqrt{6}$
C. $2\sqrt{6}$
D. 5
E. $5+2\sqrt{6}$
Pembahasan:
$\underset{x\to 5}{\mathop{\lim }}\,\frac{\sqrt{x+2\sqrt{x+1}}}{\sqrt{x-2\sqrt{x+1}}}$
$=\frac{\sqrt{5+2\sqrt{6}}}{\sqrt{5-2\sqrt{6}}}$
$=\frac{\sqrt{(3+2)+2\sqrt{3.2}}}{\sqrt{(3+2)-2\sqrt{3.2}}}$
$=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$
$=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\times \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}$
$=5+2\sqrt{6}$
Jawaban: E
Matematika Dasar SIMAK UI 2013 No. 12
Sebuah matriks disebut matriks orthogonal jika ${{A}^{-1}}={{A}^{T}}$. Jika diketahui $A=\left( \begin{matrix} a & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & b & \frac{1}{3} \\ -\frac{2}{3} & -\frac{1}{3} & c \\ \end{matrix} \right)$ maka ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}$ = …
A. -1 B. 0 C. $\frac{1}{9}$ D. $\frac{4}{9}$ E. 1
Pembahasan:
${{A}^{-1}}={{A}^{T}}$
$A.{{A}^{T}}=A.{{A}^{-1}}$
$A.{{A}^{T}}=I$
$\left( \begin{matrix} a & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & b & \frac{1}{3} \\ -\frac{2}{3} & -\frac{1}{3} & c \\ \end{matrix} \right).\left( \begin{matrix} a & \frac{2}{3} & -\frac{2}{3} \\ \frac{2}{3} & b & -\frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} & c \\ \end{matrix} \right)=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right)$
${{a}^{2}}+\frac{4}{9}+\frac{4}{9}=1\to {{a}^{2}}=\frac{1}{9}$
$\frac{4}{9}+{{b}^{2}}+\frac{1}{9}=1\to {{b}^{2}}=\frac{4}{9}$
$\frac{4}{9}+\frac{1}{9}+{{c}^{2}}=1\to {{c}^{2}}=\frac{4}{9}$
${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=\frac{1}{9}+\frac{4}{9}+\frac{4}{9}=1$
Jawaban: E
Matematika Dasar SIMAK UI 2013 No. 13
Diketahui sebuah data terdiri dari $n$ bilangan asli yang pertama. Jika salah satu data dihapus, rata-rata data yang tersisa adalah $\frac{61}{4}$. Bilangan yang dihapus tersebut adalah …
A. 8 B. 9 C. 10 D. 11 E. 12
Pembahasan:
Sn adalah jumlah n bilangan asli yang pertama $Sn=\frac{n(n+1)}{2}$.
Misal: data yang terhapus = x
${{\bar{x}}_{baru}}=\frac{\frac{n(n+1)}{2}-x}{n-1}=\frac{61}{4}$
$2{{n}^{2}}+2n-4x=61n-61$
$2{{n}^{2}}-59n+61-4x=0$
Ambil x = 8, maka:
$2{{n}^{2}}-59n+61-4.8=0$
$2{{n}^{2}}-59n+29=0$
$(2n-1)(n-29)=0$
$n=29$
Sehingga data yang terhapus x = 8.
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 14
Diketahui $y$ adalah bilangan real terkecil yang merupakan penyelesaian dari pertidaksamaan $\sqrt{\frac{1}{{{x}^{2}}}-\frac{3}{4}} > \frac{1}{x}-\frac{1}{2}$. Nilai $y$ juga memenuhi pertidaksamaan berikut, kecuali …
A. $3+\frac{3}{2}y > 1$
B. $6-2y > 1$
C. $6y-3 < 1$
D. $3{{y}^{2}}+y > 1$
E. $6{{y}^{2}}-y < 1$
Pembahasan:
$\sqrt{\frac{1}{{{x}^{2}}}-\frac{3}{4}} > \frac{1}{x}-\frac{1}{2}$ (kuadratkan kedua ruas)
$\frac{1}{{{x}^{2}}}-\frac{3}{4} > \frac{1}{{{x}^{2}}}-\frac{1}{x}+\frac{1}{4}$
$\frac{1}{x}-1 > 0$
$\frac{1-x}{x} > 0$
$0 < x < 1$
$y$ adalah $x$ terkecil maka $y\cong 0$
Dari option yang diberikan, maka yang tidak memenuhi adalah option D.
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 15
Diketahui bahwa salah satu sisi persegi ABCD menyinggung lingkaran ${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$ pada titik $(1,2)$. Dua titik sudut dari persegi tersebut terletak pada lingkaran ${{x}^{2}}+{{y}^{2}}-2x-2y-7=0$. Luas persegi ABCD adalah …
A. $\frac{32}{25}(1-\sqrt{11})$
B. $\frac{32}{25}(\sqrt{11}-6)$
C. $\frac{32}{25}(\sqrt{11}-1)$
D. $\frac{32}{25}(6-\sqrt{11})$
E. $\frac{32}{5}(\sqrt{11}-1)$
Pembahasan:
${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$
${{(x-1)}^{2}}+{{(y-1)}^{2}}=1$, diperoleh:
Titik pusat (1,1) dan jari-jari (r) = 1.
${{x}^{2}}+{{y}^{2}}-2x-2y-7=0$
${{(x-1)}^{2}}+{{(y-1)}^{2}}=9$, diperoleh:
Titik pusat (1,1) dan jari-jari (R) = 3
Perhatikan gambar berikut ini.

Misal, panjang sisi persegi ABCD adalah s, maka: BC = s, AB = s, PQ = $\frac{AB}{2}=\frac{s}{2}$
Perhatikan segitiga PQC siku-siku di titik Q, berlaku teorema phythagoras:
$P{{Q}^{2}}+Q{{C}^{2}}=P{{C}^{2}}$
${{\left( \frac{s}{2} \right)}^{2}}+{{(s+1)}^{2}}={{3}^{2}}$
$\frac{{{s}^{2}}}{4}+{{s}^{2}}+2s+1=9$
$\frac{{{s}^{2}}}{4}+{{s}^{2}}+2s-8=0$ kali 4
${{s}^{2}}+4{{s}^{2}}+8s-32=0$
$5{{s}^{2}}+8s-32=0$
$s=\frac{-8+\sqrt{{{8}^{2}}-4.5.(-32)}}{2.5}$
$s=\frac{-8+\sqrt{704}}{10}$
$s=\frac{-8+8\sqrt{11}}{10}$
$s=\frac{-4+4\sqrt{11}}{5}$
Luas = ${{s}^{2}}$
$={{\left( \frac{-4+4\sqrt{11}}{5} \right)}^{2}}$
$=\frac{16-32\sqrt{11}+176}{25}$
$=\frac{192-32\sqrt{11}}{25}$
$=\frac{32}{25}(6-\sqrt{11})$
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 16
Bilangan bulat positif terkecil $n$ yang memenuhi pertidaksamaan $\sqrt{n}-\sqrt{n-1} < 0,01$ adalah …
A. 2499
B. 2500
C. 2501
D. 10000
E. tidak ada bilangan bulat yang memenuhi.
Pembahasan:
$\sqrt{n}-\sqrt{n-1} < 0,01$
$n-2\sqrt{n(n-1)}+n-1 < 0,0001$
$2n-2\sqrt{{{n}^{2}}-n} < 1,0001$
$2n-1,0001 < 2\sqrt{{{n}^{2}}-n}$
$4{{n}^{2}}-(4,0004)n+{{(1,0001)}^{2}} < 4{{n}^{2}}-4n$
$(0,0004)n > {{(1,0001)}^{2}}$
$n > {{\left( \frac{10001}{10000} \right)}^{2}}.\frac{10000}{4}$
$n > 2500,5$
$n$ bilangan bulat positif terkecil adalah 2501.
Jawaban: C
Gunakan petunjuk C dalam menjawab soal nomor 17 sampai nomor 20.
Matematika Dasar SIMAK UI 2013 No. 17
Diketahui bahwa $n$ adalah bilangan asli. Misalkan S(n) menyatakan jumlah setiap digit $n$ (sebagai contoh: $n=1234$, S(1234) = 1 + 2 + 3 + 4 = 10), maka nilai S(S(n)) yang memenuhi persamaan $n+S(n)+S(S(n))=2013$ adalah …
(1) 2 (2) 5 (3) 8 (4) 20
Pembahasan:
$n+S(n)+S(S(n))=2013$
$n+S(n)+S(S(n))=2013$
Ambil $n=1991$, maka:
$S(1991)=1+9+9+1=20$
$S(S(n))=S(20)=2+0=2$
(1) $1991+20+2=2013$ BENAR
(2) 2003 + 5 + 5 = 2013 BENAR
(3) 1979 + 26 + 8 = 2013 BENAR
(4) tidak ada nilai yang memenuhi.
(1), (2), dan (3) BENAR
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 18
Untuk setiap $x$ dan $y$ anggota bilangan real berlaku sebuah system persamaan sebagai berikut.
$\left\{ \begin{matrix} x=2{{x}^{2}}+3{{y}^{2}} \\ y=4xy \\ \end{matrix} \right.$
Nilai $x+y$ = …
(1) 0
(2) $\frac{1}{4}-\frac{1}{12}\sqrt{6}$
(3) $\frac{1}{2}$
(4) $\frac{1}{4}+\frac{1}{12}\sqrt{6}$
Pembahasan:
Dari persamaan:
$y=4xy$
$y-4y=0$
$y(1-4x)=0\Rightarrow y=0\vee x=\frac{1}{4}$
$x+y=\frac{1}{4}+0=\frac{1}{4}$
Untuk $x=\frac{1}{4}$ substitusi ke:
$x=2{{x}^{2}}+3{{y}^{2}}$
$\frac{1}{4}=2.{{\left( \frac{1}{4} \right)}^{2}}+3{{y}^{2}}$
$\frac{1}{8}=3{{y}^{2}}\Rightarrow {{y}^{2}}=\frac{1}{24}\Rightarrow y=\pm \frac{1}{12}\sqrt{6}$
Sehingga:
$x+y=\frac{1}{4}+\frac{1}{12}\sqrt{6}$ dan $x+y=\frac{1}{4}-\frac{1}{12}\sqrt{6}$ diperoleh pernyataan (2) dan (4) BENAR.
Untuk y = 0 substitusi ke:
$x=2{{x}^{2}}+3{{y}^{2}}$
$x=2{{x}^{2}}+{{3.0}^{2}}$
$2{{x}^{2}}-x=0$
$x(2x-1)=0\Rightarrow x=0\vee x=\frac{1}{2}$
Maka:
$x+y=0+0=0$ diperoleh pernyatan (1) BENAR
$x+y=\frac{1}{2}+0=\frac{1}{2}$ diperoleh pernyataan (3) BENAR.
Jawaban: E
Matematika Dasar SIMAK UI 2013 No. 19
Jika diketahui bahwa ${{2}^{\cos 2x}}+{{2}^{{{\cos }^{2}}x}}={{3.2}^{-\cos 2x}}$, nilai $x$ adalah …
(1) $\frac{\pi }{2}$ (2) $\frac{\pi }{3}$ (3) $\frac{3\pi }{2}$ (4) $\pi $
Pembahasan:
${{2}^{\cos 2x}}+{{2}^{{{\cos }^{2}}x}}={{3.2}^{-\cos 2x}}$
${{2}^{2{{\cos }^{2}}x-1}}+{{2}^{{{\cos }^{2}}x}}=\frac{3}{2}$
$\frac{1}{2}{{.2}^{2.{{\cos }^{2}}x}}+{{2}^{{{\cos }^{2}}x}}=\frac{3}{2}$
$\frac{1}{2}{{\left( {{2}^{{{\cos }^{2}}x}} \right)}^{2}}+{{2}^{{{\cos }^{2}}x}}=\frac{3}{2}$
Misal: ${{2}^{{{\cos }^{2}}x}}=p$ dan $p > 0$ maka:
$\frac{1}{2}{{p}^{2}}+p=\frac{3}{2}$
${{p}^{2}}+2p-3=0$
$(p+3)(p-1)=0$
$p=1$
${{2}^{{{\cos }^{2}}x}}=1$
${{2}^{{{\cos }^{2}}x}}={{2}^{0}}\Rightarrow {{\cos }^{2}}x=0$
${{x}_{1}}=\frac{\pi }{2}$ atau ${{x}_{2}}=\frac{3\pi }{2}$ diperoleh pernyataan (1) dan (3) BENAR.
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 20
Diketahui $f'(x)={{x}^{3}}{{(x-a)}^{2}}(x-b)$ dengan $a < x < b$. Pernyataan yang BENAR mengenai fungsi $f$ adalah …
(1) Jika $x < b$, $f(a)$ adalah nilai maksimum $f$.
(2) Jika $x < 0$, $f(b)$ adalah nilai maksimum $f$.
(3) Jika $x < 0$, $f$ merupakan fungsi turun.
(3) Jika $x < b$, $f$ merupakan fungsi naik.
Pembahasan:
$f'(x)={{x}^{3}}{{(x-a)}^{2}}(x-b)$
$0 < a < b$
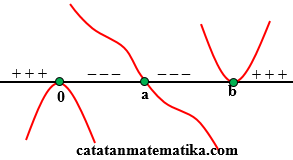
Stasioner maka $f'(x)=0$
(1) SALAH, seharusnya $f(a)$ adalah titik belok.
(2) BENAR
(3) SALAH, seharusnya $f$ merupakan fungsi naik.
(4) BENAR
Jawaban: C
Matematika Dasar SIMAK UI 2013 No. 1
Dari 26 huruf alphabet dipilih satu per satu 8 huruf sembarang dengan cara pengembalian dan disusun sehingga membentuk kata. Probabilitas bahwa di antara kata-kata yang terbentuk mengandung subkata “SIMAKUI” dalam satu rangkaian kata yang tidak terpisah adalah ….
A. $\frac{26}{{{26}^{8}}}$ B. $\frac{52}{{{26}^{8}}}$ C. $\frac{26}{\left( \begin{matrix} 26 \\ 8 \\ \end{matrix} \right)}$ D. $\frac{52}{\left( \begin{matrix} 26 \\ 8 \\ \end{matrix} \right)}$ E. $\frac{1}{8}$
Pembahasan:
n(A) = banyak susunan 8 huruf yang didalamnya mengandung subkat “SIMAKUI”. Kemungkinannya ada 2 yaitu:

Kotak merah diisikan salah satu huruf dari 26 huruf alphabet, maka diperoleh:
n(A) = 2 x 26 = 52
n(S) = banyak susunan 8 huruf sembarang dari 26 huruf = ${{26}^{8}}$.
$P(A)=\frac{n(A)}{n(S)}=\frac{52}{{{26}^{8}}}$
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 2
Jika ${}^{2}\log {{(}^{3}}\log {{(}^{4}}\log x))$ = $^{3}\log {{(}^{4}}\log {{(}^{2}}\log y))$ = $^{4}\log {{(}^{2}}\log {{(}^{3}}\log z))$ = 0, Nilai dari $x+y+z$ = …
A. 50 B. 58 C. 89 D. 111 E. 1296
Pembahasan:
*)
${}^{2}\log {{(}^{3}}\log {{(}^{4}}\log x))=0$
$^{3}\log {{(}^{4}}\log x)={{2}^{0}}$
$^{3}\log {{(}^{4}}\log x)=1$
$^{4}\log x={{3}^{1}}$
$x={{4}^{3}}=64$
*)
$^{3}\log {{(}^{4}}\log {{(}^{2}}\log y))=0$
$^{4}\log {{(}^{2}}\log y)={{3}^{0}}$
$^{4}\log {{(}^{2}}\log y)=1$
$^{2}\log y={{4}^{1}}$
$y={{2}^{4}}=16$
*)
$^{4}\log {{(}^{2}}\log {{(}^{3}}\log z))=0$
$^{2}\log {{(}^{3}}\log z)={{4}^{0}}$
$^{2}\log {{(}^{3}}\log z)=1$
$^{3}\log z={{2}^{1}}$
$z={{3}^{2}}=9$
*) maka $x+y+z=64+16+9=89$.
Jawaban: C
Matematika Dasar SIMAK UI 2013 No. 3
Diketahui bahwa $f(x)=mz+n$ dan $g(z)=pz+q$ untuk $m,n,p,q\in R$. Dengan demikian, $f(g(x))=g(f(x))$ akan memiliki solusi untuk …
A. jika dan hanya jika $n(1-p)-q(1-m)=0$.
B. jika dan hanya jika $(1-n)(1-p)-(1-q)(1-m)=0$
C. jika dan hanya jika $m=p$ dan $n=q$.
D. jika dan hanya jika $mq-np=0$
E. setiap pilihan $m,n,p,q$.
Pembahasan:
$f(g(x))=g(f(x))$
$f(px+q)=g(mx+n)$
$m(px+q)+n=p(mx+n)+q$
$mpx+mq+n=pmx+pn+q$
$mq+n=pn+q$
$n-pn=q-mq$
$n(1-p)=(1-m)q$
$n(1-p)-(1-m)q=0$
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 4
Jika r dan s adalah akar-akar persamaan $a{{x}^{2}}+bx+c=0$ dan D adalah diskriminan dari persamaan tersebut, nilai dari $\frac{1}{{{r}^{2}}}+\frac{1}{{{s}^{2}}}$ adalah …
A. $\frac{D}{{{c}^{2}}}+\frac{2a}{c}$
B. $\frac{D}{2a}+c$
C. $\frac{D}{{{c}^{2}}}$
D. $\frac{D}{2a}$
E. $D$
Pembahasan:
$a{{x}^{2}}+bx+c=0$, akar-akarnya r dan s, maka:
$r+s=\frac{-b}{a}$ dan $r.s=\frac{c}{a}$
$D={{b}^{2}}-4ac$
$\frac{1}{{{r}^{2}}}+\frac{1}{{{s}^{2}}}=\frac{{{r}^{2}}+{{s}^{2}}}{{{r}^{2}}{{s}^{2}}}$
$=\frac{{{(r+s)}^{2}}-2rs}{{{(rs)}^{2}}}$
$=\frac{{{\left( \frac{-b}{a} \right)}^{2}}-2.\frac{c}{a}}{{{\left( \frac{c}{a} \right)}^{2}}}$
$=\frac{\frac{{{b}^{2}}}{{{a}^{2}}}-\frac{2c}{a}}{\frac{{{c}^{2}}}{{{a}^{2}}}}$
$=\frac{{{b}^{2}}-2ac}{{{a}^{2}}}\times \frac{{{a}^{2}}}{{{c}^{2}}}$
$=\frac{{{b}^{2}}-2ac}{{{c}^{2}}}$
$=\frac{{{b}^{2}}-4ac}{{{c}^{2}}}+\frac{2ac}{{{c}^{2}}}$
$=\frac{D}{{{c}^{2}}}+\frac{2a}{c}$
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 5
Jika diketahui bahwa $x=\frac{1}{2013}-\frac{2}{2013}+\frac{3}{2013}-\frac{4}{2013}+...-\frac{2012}{2013}$, nilai $x$ yang memenuhi adalah …
A. $-\frac{1007}{2013}$
B. $-\frac{1006}{2013}$
C. $\frac{1}{2013}$
D. $\frac{1006}{2013}$
E. $\frac{1007}{2013}$
Pembahasan:
$1-2+3-4+...+2011-2012$
$=(1-2)+(3-4)+...+(2011-2012)$
$=(-1)+(-1)+...+(-1)$ {sebanyak 1006}
Maka:
$1-2+3-4+...-2012=(-1).1006=-1006$
$x=\frac{1}{2013}-\frac{2}{2013}+\frac{3}{2013}-\frac{4}{2013}+...-\frac{2012}{2013}$
$x=\frac{1-2+3-4+...-2012}{2013}$
$x=\frac{-1006}{2013}$
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 6
Diketahui bahwa ${{2}^{w}}.{{a}^{x}}.{{b}^{y}}.{{c}^{z}}=2013$ untuk setiap a, b, c, d, x, y, z merupakan bilangan bulat positif dan w bilangan bulat nonnegative dengan $a < b < c$. Nilai $2w+ax+by+cz$ = …
A. 0 B. 3 C. 11 D. 75 E. 611
Pembahasan:
${{2}^{w}}.{{a}^{x}}.{{b}^{y}}.{{c}^{z}}=2013$
Factor dari 2013 adalah 3, 11, dan 61 sehingga:
${{2}^{0}}{{.3}^{1}}{{.11}^{1}}{{.61}^{1}}=2013$
${{2}^{0}}{{.3}^{1}}{{.11}^{1}}{{.61}^{1}}={{2}^{w}}.{{a}^{x}}.{{b}^{y}}.{{c}^{z}}$
$w=0$, $a=3$, $x=1$, $b=11$, $y=1$, $c=61$, $z=1$
$2w+ax+by+cz=2.0+3.1+11.1+61.1=75$
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 7
Perhatikan gambar berikut ini.

Himpunan penyelesaian system pertidaksamaan , , , adalah …
A. I B. II C. III D. IV E. V
Pembahasan:

Maka daerah penyelesaiannya adalah II.
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 8
Bilangan bulat terbesar $a$ sehingga hanya terdapat tiga pasangan bilangan bulat $(x,y)$ yang memenuhi system pertidaksamaan berikut:
$\left\{ \begin{matrix} 3y-x < 5 \\ y+ax < 11 \\ 4y+x > 9 \\ \end{matrix} \right.$
adalah …
A. -1 B. 0 C. 1 D. 2 E. 3
Pembahasan:

Tiga pasangan (x,y) bilangan bulat yang memenuhi sistem yaitu:
$(2,2)$, $(3,2)$, $(4,2)$
Substitusi ke: $y+ax < 11$
$(2,2)\to 2+2a < 11 \Leftrightarrow a < \frac{9}{2}=\{...,1,2,3,4\}$
$(3,2)\to 2+3a < 11 \Leftrightarrow a < 3=\{...,1,2\}$
$(4,2)\to 2+4a < 11 \Leftrightarrow a < \frac{9}{4}=\{...,1,2\}$
Sehingga nilai a terbesar adalah 2.
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 9
Jika $A=\left[ \begin{matrix} 4 & 3 \\ 2 & 5 \\ \end{matrix} \right]$ dan ${{A}^{2}}-xA+yI=\left[ \begin{matrix} 0 & 0 \\ 0 & 0 \\ \end{matrix} \right]$ maka $x+y$ = …
A. 9 B. 14 C. 19 D. 23 E. 25
Pembahasan:
${{A}^{2}}-xA+yI=\left[ \begin{matrix} 0 & 0 \\ 0 & 0 \\ \end{matrix} \right]$
${{A}^{2}}-xA+yI=0$
${{A}^{2}}=xA-yI$
${{\left[ \begin{matrix} 4 & 3 \\ 2 & 5 \\ \end{matrix} \right]}^{2}}=x\left[ \begin{matrix} 4 & 3 \\ 2 & 5 \\ \end{matrix} \right]-y\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right]$
$\left[ \begin{matrix} 22 & 27 \\ 18 & 31 \\ \end{matrix} \right]=\left[ \begin{matrix} 4x & 3x \\ 2x & 5x \\ \end{matrix} \right]-\left[ \begin{matrix} y & 0 \\ 0 & y \\ \end{matrix} \right]$
$\left[ \begin{matrix} 22 & 27 \\ 18 & 31 \\ \end{matrix} \right]=\left[ \begin{matrix} 4x-y & 3x \\ 2x & 5x-y \\ \end{matrix} \right]$
$3x=27\to x=9$
$4x-y=22\Leftrightarrow 4.9-y=22\Leftrightarrow y=14$
$x+y=9+14=23$
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 10
Diketahui bilangan $a,b,c$ membentuk barisan geometri. Bilangan $a,b,c-2$ membentuk barisan aritmetika dan bilangan $a,b+2,c+10$ membentuk barisan geometri. Jumlah semua nilai yang mungkin untuk $b$ adalah …
A. $\frac{14}{9}$ B. $\frac{20}{9}$ C. $\frac{32}{9}$ D. $\frac{40}{9}$ E. $\frac{80}{9}$
Pembahasan:
Barisan Geometri:
$a,b,c\Rightarrow {{b}^{2}}=ac$ …. (1)
Barisan Aritmetika:
$a,b,c-2\Rightarrow 2b=a+c-2$ …. (2)
Barisan Geometri:
$a,b+2,c+10$ maka:
${{(b+2)}^{2}}=a(c+10)$
${{b}^{2}}+4b+4=ac+10a$
${{b}^{2}}+4b+4={{b}^{2}}+10a$
$4b+4=10a$
$2b+2=5a$ …. (3)
Substitusi (2) ke (3), diperoleh:
$a+c-2+2=5a$
$c=4a$ substitusi ke (1)
${{b}^{2}}=ac\Leftrightarrow {{b}^{2}}=a.4a\Leftrightarrow b=\pm 2a$
Substitusi ke persamaan (3)
Untuk $b=2a$ maka:
$2b+2=5a$
$2.2a+2=5a$
$4a+2=5a$
$a=2$
$b=2a\to {{b}_{1}}=2.2=4$
Untuk $b=-2a$ maka:
$2b+2=5a$
$2(-2a)+2=5a$
$-4a+2=5a$
$a=\frac{2}{9}$
$b=-2a\to {{b}_{2}}=-2.\frac{2}{9}=-\frac{4}{9}$
${{b}_{1}}+{{b}_{2}}=4-\frac{4}{9}=\frac{32}{9}$
Jawaban: C
Matematika Dasar SIMAK UI 2013 No. 11
$\underset{x\to 5}{\mathop{\lim }}\,\frac{\sqrt{x+2\sqrt{x+1}}}{\sqrt{x-2\sqrt{x+1}}}=...$
A. $\sqrt{3}+\sqrt{2}$
B. $5-2\sqrt{6}$
C. $2\sqrt{6}$
D. 5
E. $5+2\sqrt{6}$
Pembahasan:
$\underset{x\to 5}{\mathop{\lim }}\,\frac{\sqrt{x+2\sqrt{x+1}}}{\sqrt{x-2\sqrt{x+1}}}$
$=\frac{\sqrt{5+2\sqrt{6}}}{\sqrt{5-2\sqrt{6}}}$
$=\frac{\sqrt{(3+2)+2\sqrt{3.2}}}{\sqrt{(3+2)-2\sqrt{3.2}}}$
$=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$
$=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\times \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}$
$=5+2\sqrt{6}$
Jawaban: E
Matematika Dasar SIMAK UI 2013 No. 12
Sebuah matriks disebut matriks orthogonal jika ${{A}^{-1}}={{A}^{T}}$. Jika diketahui $A=\left( \begin{matrix} a & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & b & \frac{1}{3} \\ -\frac{2}{3} & -\frac{1}{3} & c \\ \end{matrix} \right)$ maka ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}$ = …
A. -1 B. 0 C. $\frac{1}{9}$ D. $\frac{4}{9}$ E. 1
Pembahasan:
${{A}^{-1}}={{A}^{T}}$
$A.{{A}^{T}}=A.{{A}^{-1}}$
$A.{{A}^{T}}=I$
$\left( \begin{matrix} a & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & b & \frac{1}{3} \\ -\frac{2}{3} & -\frac{1}{3} & c \\ \end{matrix} \right).\left( \begin{matrix} a & \frac{2}{3} & -\frac{2}{3} \\ \frac{2}{3} & b & -\frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} & c \\ \end{matrix} \right)=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right)$
${{a}^{2}}+\frac{4}{9}+\frac{4}{9}=1\to {{a}^{2}}=\frac{1}{9}$
$\frac{4}{9}+{{b}^{2}}+\frac{1}{9}=1\to {{b}^{2}}=\frac{4}{9}$
$\frac{4}{9}+\frac{1}{9}+{{c}^{2}}=1\to {{c}^{2}}=\frac{4}{9}$
${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=\frac{1}{9}+\frac{4}{9}+\frac{4}{9}=1$
Jawaban: E
Matematika Dasar SIMAK UI 2013 No. 13
Diketahui sebuah data terdiri dari $n$ bilangan asli yang pertama. Jika salah satu data dihapus, rata-rata data yang tersisa adalah $\frac{61}{4}$. Bilangan yang dihapus tersebut adalah …
A. 8 B. 9 C. 10 D. 11 E. 12
Pembahasan:
Sn adalah jumlah n bilangan asli yang pertama $Sn=\frac{n(n+1)}{2}$.
Misal: data yang terhapus = x
${{\bar{x}}_{baru}}=\frac{\frac{n(n+1)}{2}-x}{n-1}=\frac{61}{4}$
$2{{n}^{2}}+2n-4x=61n-61$
$2{{n}^{2}}-59n+61-4x=0$
Ambil x = 8, maka:
$2{{n}^{2}}-59n+61-4.8=0$
$2{{n}^{2}}-59n+29=0$
$(2n-1)(n-29)=0$
$n=29$
Sehingga data yang terhapus x = 8.
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 14
Diketahui $y$ adalah bilangan real terkecil yang merupakan penyelesaian dari pertidaksamaan $\sqrt{\frac{1}{{{x}^{2}}}-\frac{3}{4}} > \frac{1}{x}-\frac{1}{2}$. Nilai $y$ juga memenuhi pertidaksamaan berikut, kecuali …
A. $3+\frac{3}{2}y > 1$
B. $6-2y > 1$
C. $6y-3 < 1$
D. $3{{y}^{2}}+y > 1$
E. $6{{y}^{2}}-y < 1$
Pembahasan:
$\sqrt{\frac{1}{{{x}^{2}}}-\frac{3}{4}} > \frac{1}{x}-\frac{1}{2}$ (kuadratkan kedua ruas)
$\frac{1}{{{x}^{2}}}-\frac{3}{4} > \frac{1}{{{x}^{2}}}-\frac{1}{x}+\frac{1}{4}$
$\frac{1}{x}-1 > 0$
$\frac{1-x}{x} > 0$
$0 < x < 1$
$y$ adalah $x$ terkecil maka $y\cong 0$
Dari option yang diberikan, maka yang tidak memenuhi adalah option D.
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 15
Diketahui bahwa salah satu sisi persegi ABCD menyinggung lingkaran ${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$ pada titik $(1,2)$. Dua titik sudut dari persegi tersebut terletak pada lingkaran ${{x}^{2}}+{{y}^{2}}-2x-2y-7=0$. Luas persegi ABCD adalah …
A. $\frac{32}{25}(1-\sqrt{11})$
B. $\frac{32}{25}(\sqrt{11}-6)$
C. $\frac{32}{25}(\sqrt{11}-1)$
D. $\frac{32}{25}(6-\sqrt{11})$
E. $\frac{32}{5}(\sqrt{11}-1)$
Pembahasan:
${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$
${{(x-1)}^{2}}+{{(y-1)}^{2}}=1$, diperoleh:
Titik pusat (1,1) dan jari-jari (r) = 1.
${{x}^{2}}+{{y}^{2}}-2x-2y-7=0$
${{(x-1)}^{2}}+{{(y-1)}^{2}}=9$, diperoleh:
Titik pusat (1,1) dan jari-jari (R) = 3
Perhatikan gambar berikut ini.

Misal, panjang sisi persegi ABCD adalah s, maka: BC = s, AB = s, PQ = $\frac{AB}{2}=\frac{s}{2}$
Perhatikan segitiga PQC siku-siku di titik Q, berlaku teorema phythagoras:
$P{{Q}^{2}}+Q{{C}^{2}}=P{{C}^{2}}$
${{\left( \frac{s}{2} \right)}^{2}}+{{(s+1)}^{2}}={{3}^{2}}$
$\frac{{{s}^{2}}}{4}+{{s}^{2}}+2s+1=9$
$\frac{{{s}^{2}}}{4}+{{s}^{2}}+2s-8=0$ kali 4
${{s}^{2}}+4{{s}^{2}}+8s-32=0$
$5{{s}^{2}}+8s-32=0$
$s=\frac{-8+\sqrt{{{8}^{2}}-4.5.(-32)}}{2.5}$
$s=\frac{-8+\sqrt{704}}{10}$
$s=\frac{-8+8\sqrt{11}}{10}$
$s=\frac{-4+4\sqrt{11}}{5}$
Luas = ${{s}^{2}}$
$={{\left( \frac{-4+4\sqrt{11}}{5} \right)}^{2}}$
$=\frac{16-32\sqrt{11}+176}{25}$
$=\frac{192-32\sqrt{11}}{25}$
$=\frac{32}{25}(6-\sqrt{11})$
Jawaban: D
Matematika Dasar SIMAK UI 2013 No. 16
Bilangan bulat positif terkecil $n$ yang memenuhi pertidaksamaan $\sqrt{n}-\sqrt{n-1} < 0,01$ adalah …
A. 2499
B. 2500
C. 2501
D. 10000
E. tidak ada bilangan bulat yang memenuhi.
Pembahasan:
$\sqrt{n}-\sqrt{n-1} < 0,01$
$n-2\sqrt{n(n-1)}+n-1 < 0,0001$
$2n-2\sqrt{{{n}^{2}}-n} < 1,0001$
$2n-1,0001 < 2\sqrt{{{n}^{2}}-n}$
$4{{n}^{2}}-(4,0004)n+{{(1,0001)}^{2}} < 4{{n}^{2}}-4n$
$(0,0004)n > {{(1,0001)}^{2}}$
$n > {{\left( \frac{10001}{10000} \right)}^{2}}.\frac{10000}{4}$
$n > 2500,5$
$n$ bilangan bulat positif terkecil adalah 2501.
Jawaban: C
Gunakan petunjuk C dalam menjawab soal nomor 17 sampai nomor 20.
Matematika Dasar SIMAK UI 2013 No. 17
Diketahui bahwa $n$ adalah bilangan asli. Misalkan S(n) menyatakan jumlah setiap digit $n$ (sebagai contoh: $n=1234$, S(1234) = 1 + 2 + 3 + 4 = 10), maka nilai S(S(n)) yang memenuhi persamaan $n+S(n)+S(S(n))=2013$ adalah …
(1) 2 (2) 5 (3) 8 (4) 20
Pembahasan:
$n+S(n)+S(S(n))=2013$
$n+S(n)+S(S(n))=2013$
Ambil $n=1991$, maka:
$S(1991)=1+9+9+1=20$
$S(S(n))=S(20)=2+0=2$
(1) $1991+20+2=2013$ BENAR
(2) 2003 + 5 + 5 = 2013 BENAR
(3) 1979 + 26 + 8 = 2013 BENAR
(4) tidak ada nilai yang memenuhi.
(1), (2), dan (3) BENAR
Jawaban: A
Matematika Dasar SIMAK UI 2013 No. 18
Untuk setiap $x$ dan $y$ anggota bilangan real berlaku sebuah system persamaan sebagai berikut.
$\left\{ \begin{matrix} x=2{{x}^{2}}+3{{y}^{2}} \\ y=4xy \\ \end{matrix} \right.$
Nilai $x+y$ = …
(1) 0
(2) $\frac{1}{4}-\frac{1}{12}\sqrt{6}$
(3) $\frac{1}{2}$
(4) $\frac{1}{4}+\frac{1}{12}\sqrt{6}$
Pembahasan:
Dari persamaan:
$y=4xy$
$y-4y=0$
$y(1-4x)=0\Rightarrow y=0\vee x=\frac{1}{4}$
$x+y=\frac{1}{4}+0=\frac{1}{4}$
Untuk $x=\frac{1}{4}$ substitusi ke:
$x=2{{x}^{2}}+3{{y}^{2}}$
$\frac{1}{4}=2.{{\left( \frac{1}{4} \right)}^{2}}+3{{y}^{2}}$
$\frac{1}{8}=3{{y}^{2}}\Rightarrow {{y}^{2}}=\frac{1}{24}\Rightarrow y=\pm \frac{1}{12}\sqrt{6}$
Sehingga:
$x+y=\frac{1}{4}+\frac{1}{12}\sqrt{6}$ dan $x+y=\frac{1}{4}-\frac{1}{12}\sqrt{6}$ diperoleh pernyataan (2) dan (4) BENAR.
Untuk y = 0 substitusi ke:
$x=2{{x}^{2}}+3{{y}^{2}}$
$x=2{{x}^{2}}+{{3.0}^{2}}$
$2{{x}^{2}}-x=0$
$x(2x-1)=0\Rightarrow x=0\vee x=\frac{1}{2}$
Maka:
$x+y=0+0=0$ diperoleh pernyatan (1) BENAR
$x+y=\frac{1}{2}+0=\frac{1}{2}$ diperoleh pernyataan (3) BENAR.
Jawaban: E
Matematika Dasar SIMAK UI 2013 No. 19
Jika diketahui bahwa ${{2}^{\cos 2x}}+{{2}^{{{\cos }^{2}}x}}={{3.2}^{-\cos 2x}}$, nilai $x$ adalah …
(1) $\frac{\pi }{2}$ (2) $\frac{\pi }{3}$ (3) $\frac{3\pi }{2}$ (4) $\pi $
Pembahasan:
${{2}^{\cos 2x}}+{{2}^{{{\cos }^{2}}x}}={{3.2}^{-\cos 2x}}$
${{2}^{2{{\cos }^{2}}x-1}}+{{2}^{{{\cos }^{2}}x}}=\frac{3}{2}$
$\frac{1}{2}{{.2}^{2.{{\cos }^{2}}x}}+{{2}^{{{\cos }^{2}}x}}=\frac{3}{2}$
$\frac{1}{2}{{\left( {{2}^{{{\cos }^{2}}x}} \right)}^{2}}+{{2}^{{{\cos }^{2}}x}}=\frac{3}{2}$
Misal: ${{2}^{{{\cos }^{2}}x}}=p$ dan $p > 0$ maka:
$\frac{1}{2}{{p}^{2}}+p=\frac{3}{2}$
${{p}^{2}}+2p-3=0$
$(p+3)(p-1)=0$
$p=1$
${{2}^{{{\cos }^{2}}x}}=1$
${{2}^{{{\cos }^{2}}x}}={{2}^{0}}\Rightarrow {{\cos }^{2}}x=0$
${{x}_{1}}=\frac{\pi }{2}$ atau ${{x}_{2}}=\frac{3\pi }{2}$ diperoleh pernyataan (1) dan (3) BENAR.
Jawaban: B
Matematika Dasar SIMAK UI 2013 No. 20
Diketahui $f'(x)={{x}^{3}}{{(x-a)}^{2}}(x-b)$ dengan $a < x < b$. Pernyataan yang BENAR mengenai fungsi $f$ adalah …
(1) Jika $x < b$, $f(a)$ adalah nilai maksimum $f$.
(2) Jika $x < 0$, $f(b)$ adalah nilai maksimum $f$.
(3) Jika $x < 0$, $f$ merupakan fungsi turun.
(3) Jika $x < b$, $f$ merupakan fungsi naik.
Pembahasan:
$f'(x)={{x}^{3}}{{(x-a)}^{2}}(x-b)$
$0 < a < b$

Stasioner maka $f'(x)=0$
(1) SALAH, seharusnya $f(a)$ adalah titik belok.
(2) BENAR
(3) SALAH, seharusnya $f$ merupakan fungsi naik.
(4) BENAR
Jawaban: C
Artikel Terkait:
|

Post a Comment for "Pembahasan Soal SIMAK UI 2013 Matematika Dasar"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.