Masalah Fungsi Turunan
Berikut ini masalah atau soal-soal aplikasi Fungsi Turunan.
Pembahasan:
Perhatikan gambar berikut!
Perhatikan Segitiga BFC siku-siku di C
$\sin \theta = \frac{BF}{BC} \leftrightarrow \sin \theta = \frac{y}{10} \leftrightarrow y=10 \sin \theta$
$\cos \theta = \frac{CF}{BC} \leftrightarrow \cos \theta = \frac{x}{10} \leftrightarrow x=10 \cos \theta$
Agar volume maksimum, maka luas penampang talang (berbentuk trapesium) harus maksimum.
$\begin{align} L &= \frac{jumlah \ sisi \ sejajar \times tinggi}{2} \\ &= \frac{(DC + AB) \times BF}{2} \\ &= \frac{\left( (x + 10 + x) + 10 \right) \times y}{2} \\ &= \frac{\left(2x + 20 \right) \times y}{2} \\ &= (x+10).y \\ &= (10 \cos \theta + 10).10 \sin \theta \\ &= 100 \sin \theta \cos \theta + 100 \sin \theta \\ &= 50.2 \sin \theta \cos \theta + 100 \sin \theta \\ L &= 50. \sin 2\theta + 100 \sin \theta \end{align}$
$L'=100 \cos 2\theta + 100 \cos \theta$
$L'=0$, maka:
$\begin{align} 100 \cos 2\theta + 100 \cos \theta &= 0 \\ \cos 2\theta + \cos \theta &= 0 \\ 2\cos^2 \theta -1 + \cos \theta &= 0 \\ 2\cos^2 \theta + \cos \theta -1 &= 0 \\ (2\cos \theta -1)(\cos \theta + 1) &= 0 \end{align}$
$\cos \theta = \frac{1}{2}$ atau $\cos \theta = -1$
$\cos \theta = \frac{1}{2} \leftrightarrow \theta = 60^o$
$\cos \theta = -1 \leftrightarrow \theta = 180^o$ tidak memenuhi sebab dinding talang akan berimpit dan tidak bisa menampung air.
Dengan logika sederhana maka diperoleh $\theta = 60^o$
Pembahasan:
$B(x)=x^3-600x^2+112.500.000$
$B'(x)=3x^2-1200x$
$B'(x)=0$
$3x^2-1200x=0$
$x^2-400x=0$
$x(x-400)=0$
$x=0$ atau $x=400$
Uji Turunan Kedua
$B''(x)=6x-1200$
$B''(0)=6.0-1200=-1200 \leftrightarrow B''(x) < 0$ maka diperoleh Biaya maksimum untuk $x=0$.
$B''(400)=6.400-1200=1200 \leftrightarrow B''(x) > 0$ maka diperoleh Biaya minimum untuk $x=400$.
Jadi, biaya produksi minimum ketika jumlah barang yang diproduksi 400 unit.
Penyelesaian:
Perhatikan gambar berikut!
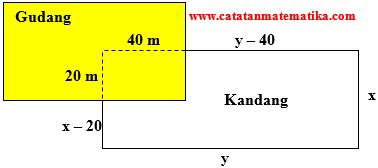
Dari gambar, kita peroleh ukuran panjang kawat duri yang dibutuhkan untuk membuat kandang adalah:
$\begin{align} x-20+y+x+y-40 &=800 \\ 2x+2y &=860 \\ x+y &=430 \\ y &=430-x \end{align}$
Luas kandang (L) adalah:
$\begin{align} L &=xy-20\times 40 \\ &= x(430-x)-800 \\ L &= -{{x}^{2}}+430x-800 \end{align}$
Luas maksimum diperoleh untuk $L'=0$
$\begin{align} L' &=-2x+430 \\ 0 &=-2x+430 \\ 2x &=430 \\ x &=215 \end{align}$
$\begin{align} y &=430-x \\ &= 430-215 \\ y &=215 \end{align}$
Jadi, ukuran kandang agar luas maksimum adalah x = 215 m dan y = 215 m.
Soal No. 1
Sebuah talang air terbuat dari lembaran seng yang lebarnya 30 cm dengan cara melipat lebarnya menjadi tiga bagian yang sama seperti terlihat pada gambar di bawah ini. Besar sudut dinding talang dengan bidang alas adalah $\theta$. Hitunglah besar sudut agar volume air yang tertampung maksium dengan terlebih dahulu membuat sketsa ukuran-ukuran yang diperlukan! Tuliskan langkah penyelesaiannya!Pembahasan:
Perhatikan gambar berikut!
Perhatikan Segitiga BFC siku-siku di C
$\sin \theta = \frac{BF}{BC} \leftrightarrow \sin \theta = \frac{y}{10} \leftrightarrow y=10 \sin \theta$
$\cos \theta = \frac{CF}{BC} \leftrightarrow \cos \theta = \frac{x}{10} \leftrightarrow x=10 \cos \theta$
Agar volume maksimum, maka luas penampang talang (berbentuk trapesium) harus maksimum.
$\begin{align} L &= \frac{jumlah \ sisi \ sejajar \times tinggi}{2} \\ &= \frac{(DC + AB) \times BF}{2} \\ &= \frac{\left( (x + 10 + x) + 10 \right) \times y}{2} \\ &= \frac{\left(2x + 20 \right) \times y}{2} \\ &= (x+10).y \\ &= (10 \cos \theta + 10).10 \sin \theta \\ &= 100 \sin \theta \cos \theta + 100 \sin \theta \\ &= 50.2 \sin \theta \cos \theta + 100 \sin \theta \\ L &= 50. \sin 2\theta + 100 \sin \theta \end{align}$
$L'=100 \cos 2\theta + 100 \cos \theta$
$L'=0$, maka:
$\begin{align} 100 \cos 2\theta + 100 \cos \theta &= 0 \\ \cos 2\theta + \cos \theta &= 0 \\ 2\cos^2 \theta -1 + \cos \theta &= 0 \\ 2\cos^2 \theta + \cos \theta -1 &= 0 \\ (2\cos \theta -1)(\cos \theta + 1) &= 0 \end{align}$
$\cos \theta = \frac{1}{2}$ atau $\cos \theta = -1$
$\cos \theta = \frac{1}{2} \leftrightarrow \theta = 60^o$
$\cos \theta = -1 \leftrightarrow \theta = 180^o$ tidak memenuhi sebab dinding talang akan berimpit dan tidak bisa menampung air.
Dengan logika sederhana maka diperoleh $\theta = 60^o$
Soal No. 2
Suatu perusahaan memproduksi x unit barang per hari dengan biaya produksi $x^3-600x^2+112.500.000$ rupiah. Tentukanlah berapa unit barang harus diproduksi setiap harinya supaya biaya produksi menjadi minimum.Pembahasan:
$B(x)=x^3-600x^2+112.500.000$
$B'(x)=3x^2-1200x$
$B'(x)=0$
$3x^2-1200x=0$
$x^2-400x=0$
$x(x-400)=0$
$x=0$ atau $x=400$
Uji Turunan Kedua
$B''(x)=6x-1200$
$B''(0)=6.0-1200=-1200 \leftrightarrow B''(x) < 0$ maka diperoleh Biaya maksimum untuk $x=0$.
$B''(400)=6.400-1200=1200 \leftrightarrow B''(x) > 0$ maka diperoleh Biaya minimum untuk $x=400$.
Jadi, biaya produksi minimum ketika jumlah barang yang diproduksi 400 unit.
Soal No. 3
Seorang petani mempunyai kawat duri sebanyak 800 m yang digunakan untuk membuat kandang siku empat untuk memenuhi pojok gudang berukuran 20 m x 40 m seperti gambar (semua pojok harus dipakai dan tidak memerlukan kawat). Berapa ukuran kandang agar luas maksimum?Penyelesaian:
Perhatikan gambar berikut!
Dari gambar, kita peroleh ukuran panjang kawat duri yang dibutuhkan untuk membuat kandang adalah:
$\begin{align} x-20+y+x+y-40 &=800 \\ 2x+2y &=860 \\ x+y &=430 \\ y &=430-x \end{align}$
Luas kandang (L) adalah:
$\begin{align} L &=xy-20\times 40 \\ &= x(430-x)-800 \\ L &= -{{x}^{2}}+430x-800 \end{align}$
Luas maksimum diperoleh untuk $L'=0$
$\begin{align} L' &=-2x+430 \\ 0 &=-2x+430 \\ 2x &=430 \\ x &=215 \end{align}$
$\begin{align} y &=430-x \\ &= 430-215 \\ y &=215 \end{align}$
Jadi, ukuran kandang agar luas maksimum adalah x = 215 m dan y = 215 m.
Semoga postingan: Masalah Fungsi Turunan ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Masalah Fungsi Turunan"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.