Barisan dan Deret Bilangan Bertingkat

Barisan bilangan adalah himpunan bilangan-bilangan yang memiliki pola atau aturan tertentu antara satu bilangan dengan bilangan berikutnya.
Bentuk Umum:
$U_1, U_2, U_3, ..., U_n$

Deret Bilangan adalah jumlah bilangan-bilangan suatu barisan bilangan.
Bentuk Umum:
$U_1 + U_2 + U_3 + ... + U_n = S_n$

Nah, yang akan kita bahas kali ini adalah barisan yang memiliki selisih (beda) tetap dan jika pada satu tingkat pengerjaan belum diperoleh selisih tetap, maka pengerjaan dilakukan pada tingkat berikutnya sampai diperoleh selisih tetap. Nah, tingkat perolehan selisih tetap ini menyatakan derajat suatu barisan. Perhatikan penjelasan berikut:

1. Jika selisih tetap diperoleh dalam satu tingkat maka barisan disebut berderajat satu (linear), yang bentuk umum suku ke-n nya adalah $U_n = pn + q$.
Contoh 1.
Barisan 4, 7, 10, 13, ... disebut berderajat satu karena selisih tetap diperoleh pada satu tingkat.


2. Jika selisih tetap diperoleh dalam dua tingkat maka barisan disebut berderajat dua, yang bentuk umum suku ke-n nya adalah $U_n = pn^2 + qn + r$.
Contoh 2.
Barisan bilangan: 8, 11, 16, 23, 32, ....


3. Jika selisih tetap diperoleh dalam tiga tingkat maka barisan disebut berderajat tiga, yang bentuk umum suku ke-n nya adalah $U_n = pn^3 + qn^2 + rn + s$.
Contoh 3.
Barisan bilangan: 7, 8, 14, 29, 57, ....

Demikian seterusnya....! Gimana paham kan? Tentu pahamlah yak... yang jelasin kan saya....! hehehehe..!

Kemudian muncul pertanyaan....! Bagaimana menentukan Rumus Suku ke-n ($U_n$) dan Jumlah n suku pertama ($S_n$) barisan tersebut. Kalau barisan bertingkat satu pasti sudah tahu ya kan....! Itu ada nama khususnya yaitu Barisan Aritmetika. Namun kita akan bahas juga dengan cara yang berbeda disini.

Baiklah...! Mari kita bahas bersama ya....., silahkan diperhatikan baik-baik ya....!
Rumus yang akan kita gunakan adalah sebagai berikut:
Rumus Suku ke-n:
$U_n = a + (n-1).a_1 + \frac{(n-1)(n-2)}{1.2}.a_2 + ... + \frac{(n-1)(n-2)(n-3)...}{1.2.3....}.a_r$
Rumus Jumlah n Suku Pertama:
$S_n = n.a + \frac{n(n-1)}{1.2}.a_1 + \frac{n(n-1)(n-2)}{1.2.3}.a_2 + ... + \frac{n(n-1)(n-2)(n-3)...}{1.2.3.4....}.a_r$

Pembahasan Contoh 1.



Rumus Suku ke-n:
$\begin{align*}U_n &= a + (n-1).a_1\\
&= 4 + (n-1).3\\
&= 4 + 3n - 3\\
U_n &= 3n + 1\end{align*}$
Jumlah n Suku Pertama:
$\begin{align*}S_n &= n.a + \frac{n(n-1)}{1.2}.a_1\\
&= n.4 + \frac{n(n-1)}{1.2}.3\\
&= 4n + \frac{3n^2-3n)}{2}\\
&= \frac{8n}{2} + \frac{3n^2-3n)}{2}\\
S_n &= \frac{3n^2+5n}{2}\end{align*}$

Pembahasan Contoh 2.

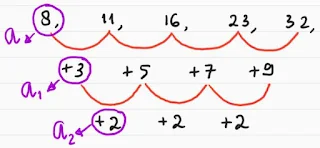
Rumus Suku ke-n:
$\begin{align*}U_n &= a + (n-1).a_1 + \frac{(n-1)(n-2)}{1.2}.a_2\\
&= 8 + (n-1).3 + \frac{(n-1)(n-2)}{1.2}.2\\
&= 8 + 3n - 3 + n^2 - 3n + 2\\
U_n &= n^2 + 7\end{align*}$
Jumlah n Suku Pertama:
$\begin{align*}S_n &= n.8 + \frac{n(n-1)}{1.2}.3 + \frac{n(n-1)(n-2)}{1.2.3}.2\\
&= 8n + \frac{3n^2-3n}{2} + \frac{2n^3 - 6n^2 + 4n}{6}\\
&= \frac{48n}{6} + \frac{9n^2-9n}{6} + \frac{2n^3-6n^2+4n}{6}\\
S_n &=\frac{1}{6}.(2n^3 + 3n^2 + 43n)\end{align*}$

Pembahasan Contoh 3.


Rumus Suku ke-n:
$\begin{align*}U_n &= a + (n-1).a_1 + \frac{(n-1)(n-2)}{1.2}.a_2 + \frac{(n-1)(n-2)(n-3)}{1.2.3}.a_3\\
&= 7 + (n-1).1 + \frac{(n-1)(n-2)}{1.2}.5 + \frac{(n-1)(n-2)(n-3)}{1.2.3}.4\\
&= 7 + n - 1 + \frac{(n^2- 3n + 2).5}{2} + \frac{(n^3- 6n^2+11n-6).4}{6}\\
U_n &= \frac{1}{6}.(4n^3-9n^2+5n+42)\end{align*}$
Jumlah n suku pertama:
$\begin{align*}S_n &= n.a + \frac{n(n-1)}{1.2}.a_1 + \frac{n(n-1)(n-2)}{1.2.3}.a_2 + \frac{n(n-1)(n-2)(n-3)}{1.2.3.4}.a_3\\
&= n.7 + \frac{n(n-1)}{1.2}.1 + \frac{n(n-1)(n-2)}{1.2.3}.5 + \frac{n(n-1)(n-2)(n-3)}{1.2.3.4}.4\\
S_n &= \frac{1}{6}.(n^4-n^3-n^2+43 n)
\end{align*}$

Semoga postingan: Barisan dan Deret Bilangan Bertingkat ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :