Kaidah Pencacahan 5. Ekspansi Binomial Newton

A. Segitiga Pascal

Perhatikan operasi aljabar berikut ini:
$(a+b)^0=1$
$(a+b)^1=a+b$
$(a+b)^2=a^2+2ab+b^2$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
$(a+b)^4$ = $a^4+4a^3b+6a^2b^2+4ab^3+b^4$
Dari operasi aljabar di atas, terlihat bahwa koefisien-koefisien memenuhi suatu aturan yang dikenal dengan Segitiga Pascal, yaitu:
$\begin{matrix} 1 \\ \begin{matrix} 1 & 1 \\ \end{matrix} \\ \begin{matrix} 1 & 2 & 1 \\ \end{matrix} \\ \begin{matrix} 1 & 3 & 3 & 1 \\ \end{matrix} \\ \begin{matrix} 1 & 4 & 6 & 4 & 1 \\ \end{matrix} \\ \begin{matrix} 1 & 5 & 10 & 10 & 5 & 1 \\ \end{matrix} \\ \end{matrix}$
Dengan demikian, kita dapat menjabarkan $(a+b)^5$ menggunakan segitiga pascal yang hasilnya sebagai berikut:

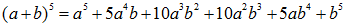
B. Binomial Newton dengan notasi kombinasi.

Segitiga pascal dapat dituliskan dengan notasi kombinasi sebagai berikut:
$\begin{matrix} \left( \begin{matrix} 0 \\ 0 \\ \end{matrix} \right) \\ \begin{matrix} \left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right) & \left( \begin{matrix} 1 \\ 1 \\ \end{matrix} \right) \\ \end{matrix} \\ \begin{matrix} \left( \begin{matrix} 2 \\ 0 \\ \end{matrix} \right) & \left( \begin{matrix} 2 \\ 1 \\ \end{matrix} \right) & \left( \begin{matrix} 2 \\ 2 \\ \end{matrix} \right) \\ \end{matrix} \\ \begin{matrix} \left( \begin{matrix} 3 \\ 0 \\ \end{matrix} \right) & \left( \begin{matrix} 3 \\ 1 \\ \end{matrix} \right) & \left( \begin{matrix} 3 \\ 2 \\ \end{matrix} \right) & \left( \begin{matrix} 3 \\ 3 \\ \end{matrix} \right) \\ \end{matrix} \\ \begin{matrix} \left( \begin{matrix} 4 \\ 0 \\ \end{matrix} \right) & \left( \begin{matrix} 4 \\ 1 \\ \end{matrix} \right) & \left( \begin{matrix} 4 \\ 2 \\ \end{matrix} \right) & \left( \begin{matrix} 4 \\ 3 \\ \end{matrix} \right) & \left( \begin{matrix} 4 \\ 4 \\ \end{matrix} \right) \\ \end{matrix} \\ \begin{matrix} \left( \begin{matrix} 5 \\ 0 \\ \end{matrix} \right) & \left( \begin{matrix} 5 \\ 1 \\ \end{matrix} \right) & \left( \begin{matrix} 5 \\ 2 \\ \end{matrix} \right) & \left( \begin{matrix} 5 \\ 3 \\ \end{matrix} \right) & \left( \begin{matrix} 5 \\ 4 \\ \end{matrix} \right) & \left( \begin{matrix} 5 \\ 5 \\ \end{matrix} \right) \\ \end{matrix} \\ \end{matrix}$
Dengan demikian, kita dapat menjabarkan $(a+b)^5$ menggunakan kombinasi yang hasilnya sebagai berikut:

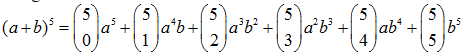
Bentuk ini disebutlah dengan Binomial Newton.

Binomial Newton, secara umum ditulis sebagai berikut:

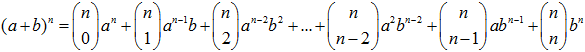
atau $(a+b)^n= \sum\limits_{r=0}^n{\left( \begin{matrix} n \\ r \\ \end{matrix} \right).a^{n-r}.b^r}$ dengan suku ke-r = $\left( \begin{matrix} n \\ r-1 \\ \end{matrix} \right)a^{n-r+1}b^{r-1}$

Contoh 1.

Hitunglah koefisien $x^6$ dari $(3x+4)^7$.
Penyelesaian:
$(3x+4)^7\to n=7$
Misalkan koefisien $x^6$ adalah $k$ dan $kx^6$ adalah suku ke-$r$ maka:
$\begin{align}kx^6 &= \left( \begin{matrix} n \\ r-1 \\ \end{matrix} \right).(3x)^{n-r+1}.4^{r-1} \\ &= \left( \begin{matrix} 7 \\ r-1 \\ \end{matrix} \right)(3x)^{7-r+1}.4^{r-1} \\ &= \left( \begin{matrix} 7 \\ r-1 \\ \end{matrix} \right)(3x)^{8-r}.4^{r-1} \\ kx^6 &= \left( \begin{matrix} 7 \\ r-1 \\ \end{matrix} \right)3^{8-r}.4^{r-1}.x^{8-r} \end{align}$
Perhatikan pangkat variabel $x$ di ruas kiri dan kanan maka:
$6=8-r\to r=2$
Substitusi $r=2$ ke persamaan:
$\begin{align}kx^6 &= \left( \begin{matrix} n \\ r-1 \\ \end{matrix} \right).(3x)^{n-r+1}.4^{r-1} \\ &= \left( \begin{matrix} 7 \\ 2-1 \\ \end{matrix} \right).(3x)^{7-2+1}.4^{2-1} \\ &= \left( \begin{matrix} 7 \\ 1 \\ \end{matrix} \right).(3x)^6.4^1 \\ &= \frac{7!}{1!.6!}\times 729\times 4x^6 \\ &= \frac{7.6!}{1!.6!}\times 729\times 4x^6 \\ kx^6 &= 20.412x^6 \\ k &= 20.412 \end{align}$
Jadi, koefisien $x^6$ dari $(3x+4)^7$ adalah 20.412.

Contoh 2.

Tentukan suku kelima dari hasil ekspansi $(x^3-2x)^6$.
Penyelesaian:
$(x^3-2x)^6\to n=6$
Suku ke-$r$ dari ekspansi ${{(a+b)}^{n}}$ adalah $\left( \begin{matrix} n \\ r-1 \\ \end{matrix} \right)a^{n-r+1}b^{r-1}$.
Suku kelima dari ekspansi $(x^3-2x)^6$ adalah:
= $\left( \begin{matrix} 6 \\ 5-1 \\ \end{matrix} \right).(x^3)^{6-5+1}.(-2x)^{5-1}$
= $\left( \begin{matrix} 6 \\ 4 \\ \end{matrix} \right).(x^3)^2.(-2x)^4$
= $\frac{6!}{4!.2!}.x^4.16x^4$
= $\frac{6.5.4!}{4!.2!}.16x^{10}$
= $240x^{10}$
Jadi, suku kelima dari ekspansi adalah $240x^{10}$

Contoh 3. Soal Olimpiade SCE USU 2016

Hitunglah koefisien $x^5y^2$ dari $(x+y^2)^6$.
Penyelesaian:
$(x+y^2)^6\to n=6$
Misalkan koefisien dari $x^5y^2$ adalah $k$ dan $kx^5y^2$ adalah suku ke-$r$, maka:
$\begin{align}kx^5y^2 &= \left( \begin{matrix} n \\ r-1 \\ \end{matrix} \right).x^{n-r+1}.(y^2)^{r-1} \\ &= \left( \begin{matrix} 6 \\ r-1 \\ \end{matrix} \right).x^{6-r+1}.(y^2)^{r-1} \\ kx^5y^2 &= \left( \begin{matrix} 6 \\ r-1 \\ \end{matrix} \right).x^{7-r}.y^{2r-2} \end{align}$
Perhatikan pangkat variabel $x$ di ruas kiri dan kanan maka:
$5=7-r\to r=2$
Substitusi $r=1$ ke persamaan:
$\begin{align}kx^5y^2 &= \left( \begin{matrix} n \\ r-1 \\ \end{matrix} \right).x^{n-r+1}.(y^2)^{r-1} \\ &= \left( \begin{matrix} 6 \\ 2-1 \\ \end{matrix} \right).x^{6-2+1}.(y^2)^{2-1} \\ &= \left( \begin{matrix} 6 \\ 1 \\ \end{matrix} \right).x^5.y^2 \\ &= \frac{6!}{1!.5!}.x^5y^2 \\ &= \frac{6.5!}{1.5!}.x^5y^2 \\ kx^5y^2 &= 6x^5y^2 \\ k &= 6 \end{align}$
Jadi, koefisien koefisien $x^5y^2$ dari $(x+y^2)^6$ adalah 6.

C. Soal Latihan

1. Tentukan koefisien $x^2y^3$ dari $(2x-y)^5$.
2. Tentukan suku kelima dari ekspansi binomial $(x+2y)^{10}$.
3. Tentukan koefisien suku ke empat dari $(x-3y)^7$.
4. Hitunglah koefisien $x^5$ dari uraian $\left( x^2+\frac{1}{2x} \right)^7$.
5. Tentukan suku keempat dari ekspansi binomial $\left( 2x^2-\frac{1}{2}y^3 \right)^8$.

Share :