Perbandingan Trigonometri Sudut Istimewa

A. Definisi Sudut Istimewa

Sudut istimewa adalah suatu sudut yang nilai perbandingan trigonometrinya dapat ditentukan secara langsung tanpa menggunakan kalkulator atau daftar trigonometri.

Sudut-sudut istimewa yang akan kita bahas adalah $0^\circ $, $30^\circ $, $45^\circ $, $60^\circ $ dan $90^\circ $.
Nilai perbandingan trigonometri untuk sudut-sudut istimewa dapat ditentukan dengan langkah-langkah sebagai berikut:

1. Lukislah lingkaran dengan pusat O(0,0) dan panjang jari-jari r satuan pada bidang kartesius.
2. Lukis titik P(x,y) pada lingkaran, proyeksikan titik P(x,y) pada sumbu X diperoleh P’(x,0).
3. Lukislah segitiga OP’P siku-siku di titik P’.
4. $ \alpha $ = sudut yaang dibentuk oleh garis OP dan OP’.

Perhatikan gambar berikut!

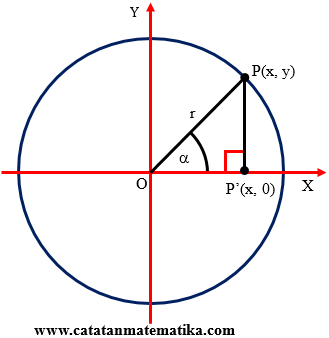
Pada segitiga OP’P maka:
$\sin \alpha =\frac{PP'}{OP}\Leftrightarrow \sin \alpha =\frac{y}{r}$
$\cos \alpha =\frac{OP'}{OP}\Leftrightarrow \cos \alpha =\frac{x}{r}$
$\tan \alpha =\frac{PP'}{OP}\Leftrightarrow \tan \alpha =\frac{y}{x}$

Kesimpulan:
Jika titik $P(x,y)$ terletak pada lingkaran berjari-jari $r$ dan $\alpha $ adalah sudut yang dibentuk oleh garis OP dan sumbu X positif maka:

• $\sin \alpha =\frac{y}{r}$
• $\cos \alpha =\frac{x}{r}$
• $\tan \alpha =\frac{y}{x}$
• $\csc \alpha =\frac{r}{y}$
• $\sec \alpha =\frac{r}{x}$
• $\cot \alpha =\frac{x}{y}$

Konsep inilah yang akan kita gunakan untuk menentukan nilai perbandingan trigonometri sudut-sudut istimewa yaitu $0^\circ $, $30^\circ $, $45^\circ $, $60^\circ $ dan $90^\circ $.

B. Nilai Perbandingan Trigonometri untuk Sudut $0^\circ $

Perhatikan gambar berikut!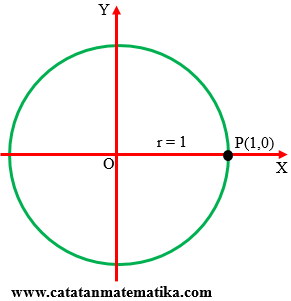

Untuk $\alpha =0{}^\circ $ diperoleh koordinat titik P(1,0) maka maka:
$x=1$, $y=0$ dan r = 1
$\sin \alpha =\sin 0^\circ =\frac{y}{r}=\frac{0}{1}=0$
$\cos \alpha =\cos 0^\circ =\frac{x}{r}=\frac{1}{1}=1$
$\tan \alpha =\tan 0^\circ =\frac{y}{x}=\frac{0}{1}=0$
$\csc \alpha =\csc 0^\circ =\frac{r}{y}=\frac{1}{0}=\sim $
$\sec \alpha =\sec 0^\circ =\frac{r}{x}=\frac{1}{1}=1$
$\cot \alpha =\cot 0^\circ =\frac{x}{y}=\frac{1}{0}=\sim $

C. Nilai Perbandingan Trigonometri untuk Sudut $30^\circ $

Perhatikan gambar berikut!

Segitiga POQ adalah segitiga sama sisi dengan OP = OQ = PQ = 1.
$\angle POQ=\angle OQP=\angle OPQ=60^\circ $.
$\begin{align} \angle POQ &= 60^\circ \\ 2\alpha &= 60^\circ \\ \alpha &= 30^\circ \end{align}$
Titik P’ adalah titik tengah PQ maka $PP'=\frac{1}{2}$ , diperoleh ordinat titik P adalah $\frac{1}{2}$.
Perhatikan segitiga OP’P siku-siku di P’:
$\begin{align} OP' &= \sqrt{OP^2-(PP')^2} \\ &= \sqrt{1^2-{\left( \frac{1}{2} \right)}^2} \\ &= \sqrt{1-\frac{1}{4}} \\ &= \sqrt{\frac{3}{4}} \\ OP' &=\frac{1}{2}\sqrt{3} \end{align}$
Jadi, untuk $\alpha =30^\circ $ diperoleh koordinat titik $P\left( \frac{1}{2}\sqrt{3},\frac{1}{2} \right)$.
$x=\frac{1}{2}\sqrt{3}$; $y=\frac{1}{2}$; dan r = 1
$\sin \alpha =\sin 30^\circ =\frac{y}{r}=\frac{\frac{1}{2}}{1}=\frac{1}{2}$
$\cos \alpha =\cos 30^\circ =\frac{x}{r}=\frac{\frac{1}{2}\sqrt{3}}{1}=\frac{1}{2}\sqrt{3}$
$\tan \alpha =\tan 30^\circ =\frac{y}{x}=\frac{\frac{1}{2}}{\frac{1}{2}\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$
$\csc \alpha =\csc 30^\circ =\frac{r}{y}=\frac{1}{\frac{1}{2}}=2$
$\sec \alpha =\sec 30^\circ =\frac{r}{x}=\frac{1}{\frac{1}{2}\sqrt{3}}=\frac{2}{\sqrt{3}}=\frac{2}{3}\sqrt{3}$
$\cot \alpha =\cot 30^\circ =\frac{x}{y}=\frac{\frac{1}{2}\sqrt{3}}{\frac{1}{2}}=\sqrt{3}$

D. Nilai Perbandingan Trigonometri untuk Sudut $45^\circ $

Perhatikan gambar berikut!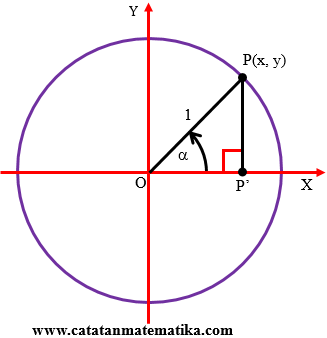

Segitiga POP’ adalah segitiga sama kaki dengan OP = PP’.
$\angle POP'=\angle OPP'=\alpha $
$\begin{align} \angle POP'+\angle POP'+\angle OP'P &= 180^\circ \\ \alpha + \alpha +90^\circ &= 180^\circ \\ 2\alpha &= 90^\circ \\ \alpha &= 45^\circ \end{align}$
Perhatikan segitiga OP’P siku-siku di P’:
$\begin{align}(OP')^2+(PP')^2 &= (OP)^2 \\ (OP')^2+(OP')^2 &= 1^2 \\ 2(OP')^2 &= 1 \\ (OP')^2 &= \frac{1}{2} \\ OP' &= \frac{1}{2}\sqrt{2} \\ PP' &= \frac{1}{2}\sqrt{2} \end{align}$
Jadi, untuk $\alpha =45^\circ $ diperoleh koordinat titik $P\left( \frac{1}{2}\sqrt{2},\frac{1}{2}\sqrt{2} \right)$.
$x=\frac{1}{2}\sqrt{2}$; $y=\frac{1}{2}\sqrt{2}$; dan r = 1
$\sin \alpha =\sin 45^\circ =\frac{y}{r}=\frac{\frac{1}{2}\sqrt{2}}{1}=\frac{1}{2}\sqrt{2}$
$\cos \alpha =\cos 45^\circ =\frac{x}{r}=\frac{\frac{1}{2}\sqrt{2}}{1}=\frac{1}{2}\sqrt{2}$
$\tan \alpha =\tan 45^\circ =\frac{y}{x}=\frac{\frac{1}{2}\sqrt{2}}{\frac{1}{2}\sqrt{2}}=1$
$\csc \alpha =\csc 45^\circ =\frac{r}{y}=\frac{1}{\frac{1}{2}\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$
$\sec \alpha =\sec 45^\circ =\frac{r}{x}=\frac{1}{\frac{1}{2}\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$
$\cot \alpha =\cot 45^\circ =\frac{x}{y}=\frac{\frac{1}{2}\sqrt{2}}{\frac{1}{2}\sqrt{2}}=1$

E. Nilai Perbandingan Trigonometri untuk Sudut $60^\circ $

Perhatikan gambar berikut!

Segitiga POQ adalah segitiga sama sisi dengan OP = PQ = OQ = 1 maka $\alpha =60^\circ $.
Garis PP’ adalah garis tinggi pada segitiga sama sisi POQ maka titik P’ membagi dua OQ, diperoleh $OP'=\frac{1}{2}$
Perhatikan segitiga OP’P siku-siku di P’:
$\begin{align}PP' &= \sqrt{(OP)^2-(OP')^2} \\ &= \sqrt{1^2-{\left( \frac{1}{2} \right)}^2} \\ &= \sqrt{1-\frac{1}{4}} \\ &= \sqrt{\frac{3}{4}} \\ PP' &=\frac{1}{2}\sqrt{3} \end{align}$
Jadi, untuk $\alpha =60^\circ $ diperoleh koordinat titik $P\left( \frac{1}{2},\frac{1}{2}\sqrt{3} \right)$.
$x=\frac{1}{2}$; $y=\frac{1}{2}\sqrt{3}$; dan r = 1
$\sin \alpha =\sin 60^\circ =\frac{y}{r}=\frac{\frac{1}{2}\sqrt{3}}{1}=\frac{1}{2}\sqrt{3}$
$\cos \alpha =\cos 60^\circ =\frac{x}{r}=\frac{\frac{1}{2}}{1}=\frac{1}{2}$
$\tan \alpha =\tan 60^\circ =\frac{y}{x}=\frac{\frac{1}{2}\sqrt{3}}{\frac{1}{2}}=\sqrt{3}$
$\csc \alpha =\csc 60^\circ =\frac{r}{y}=\frac{1}{\frac{1}{2}\sqrt{3}}=\frac{2}{\sqrt{3}}=\frac{2}{3}\sqrt{3}$
$\sec \alpha =\sec 60^\circ =\frac{r}{x}=\frac{1}{\frac{1}{2}}=2$
$\cot \alpha =\cot 60^\circ =\frac{x}{y}=\frac{\frac{1}{2}}{\frac{1}{2}\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$

F. Nilai Perbandingan Trigonometri untuk Sudut $90{}^\circ $

Perhatikan gambar berikut!

Untuk $\alpha =90^\circ $ diperoleh koordinat titik P(0,1) maka maka:
$x=0$, $y=1$ dan r = 1
$\sin \alpha =\sin 90^\circ =\frac{y}{r}=\frac{1}{1}=1$
$\cos \alpha =\cos 90^\circ =\frac{x}{r}=\frac{0}{1}=0$
$\tan \alpha =\tan 90^\circ =\frac{y}{x}=\frac{1}{0}=\tilde{\ }$
$\csc \alpha =\csc 90^\circ =\frac{r}{y}=\frac{1}{1}=1$
$\sec \alpha =\sec 90^\circ =\frac{r}{x}=\frac{1}{0}=\tilde{\ }$
$\cot \alpha =\cot 90^\circ =\frac{x}{y}=\frac{0}{1}=0$

G. Tabel Nilai Perbandingan Trigonometri Sudut-Sudut Istimewa

H. Sudut Elevasi dan Sudut Depresi

Sudut Elevasi

Sudut Elevasi adalah sudut yang dibentuk oleh arah horizontal dengan arah pandangan pengamat ke arah atas.

Sudut Depresi

Sudut Depresi adalah sudut yang dibentuk oleh arah horizontal dengan arah pandangan pengamat ke arah bawah.

Contoh 1.

Hitunglah nilai $(\tan 45^\circ +\sin 60^\circ )\cos 30^\circ $!

Penyelesaian: Lihat/Tutup

$(\tan 45^\circ +\sin 60^\circ )\cos 30^\circ $
= $\left( 1+\frac{1}{2}\sqrt{3} \right).\frac{1}{2}\sqrt{3}$
= $\frac{1}{2}\sqrt{3}+\frac{3}{4}$

---

Contoh 2.

Hitunglah nilai $\frac{\tan \frac{\pi }{4}-\sin \frac{\pi }{6}.\cos \frac{\pi }{3}}{\left( \tan \frac{\pi }{6}+\cot \frac{\pi }{3} \right)\left( \cos \frac{\pi }{6}+\sin \frac{\pi }{3} \right)}$.

Penyelesaian: Lihat/Tutup

$\frac{\tan \frac{\pi }{4}-\sin \frac{\pi }{6}.\cos \frac{\pi }{3}}{\left( \tan \frac{\pi }{6}+\cot \frac{\pi }{3} \right)\left( \cos \frac{\pi }{6}+\sin \frac{\pi }{3} \right)}$
= $\frac{\tan 45^\circ -\sin 30^\circ .\cos 60^\circ }{\left( \tan 30^\circ +\cot 60^\circ \right)\left( \cos 30^\circ +\sin 60^\circ \right)}$
= $\frac{1-\frac{1}{2}.\frac{1}{2}}{\left( \frac{1}{3}\sqrt{3}+\frac{1}{3}\sqrt{3} \right)\left( \frac{1}{2}\sqrt{3}+\frac{1}{2}\sqrt{3} \right)}$
= $\frac{1-\frac{1}{4}}{\frac{2}{3}\sqrt{3}.\sqrt{3}}$
= $\frac{\frac{3}{4}}{2}$
= $\frac{3}{8}$

---

Contoh 3.

Seorang ahli biologi berjarak 60 meter dari sebuah pohon dan melihat puncak pohon dengan sudut elevasi $30^\circ $. Jika tinggi ahli biologi 200 cm, maka tinggi pohon adalah ... meter.

Penyelesaian: Lihat/Tutup

Perhatikan gambar berikut!

$\begin{align} \tan 30^\circ &= \frac{DE}{CD} \\ \frac{1}{3}\sqrt{3} &= \frac{DE}{60} \\ DE &= 20\sqrt{3}\,\text{m} \end{align}$
AD = BC = 200 cm = 2 m
$\begin{align}\text{Tinggi}\,\text{Pohon}\, &=AD+DE \\ &= (2+20\sqrt{3}) \\ &= 36,64\,\text{m} \end{align}$
Jadi, tinggi pohon adalah 36,64 meter.

---

Contoh 4.

Dari atas gedung dengan tinggi 50 meter, b4ngrp melihat mobil bergerak ke arahnya. Pada mulanya mobil terlihat dengan sudut depresi $30{}^\circ $ dan sesaat kemudian dengan sudut $45{}^\circ $. Jika tinggi badan b4ngrp 200 cm, maka jarak yang ditempuh oleh mobil adalah ... meter.

Penyelesaian: Lihat/Tutup

Perhatikan gambar berikut!

Perhatikan segitiga ACD:
$\begin{align}\tan 30^\circ &= \frac{CD}{AC} \\ \frac{1}{\sqrt{3}} &= \frac{52}{AC} \\ AC &= 52\sqrt{3} \end{align}$
Perhatikan segitiga BCD:
$\begin{align}\tan 45^\circ &= \frac{CD}{BC} \\ 1 &=\frac{52}{BC} \\ BC &=52 \end{align}$
$\begin{align}AB &= AC-BC \\ &= (52\sqrt{3}-52) \\ AB &= 38,07 \end{align}$
Jadi, jarak yang ditempuh mobil adalah 38,07 meter.

---

Semoga postingan: Perbandingan Trigonometri Sudut Istimewa ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :