Dimensi Tiga 3. Jarak Titik ke Bidang pada Bangun Ruang

A. Definisi Jarak ke Bidang

Jarak antara titik A dan bidang $\alpha $ adalah panjang ruas garis AB, dengan titik B merupakan proyeksi titik A pada bidang $\alpha $.

Perhatikan gambar berikut:

B. Contoh Soal dan Pembahasan

No. 1 (Latihan 1.3 Matematika Wajib kelas 12)

Diketahui kubus ABCD.EFGH yang panjang rusuknya $a$ cm. Titik Q adalah titik tengah rusuk BF. Tentukan jarak titik H ke bidang ACQ.
Pembahasan:

Jarak titik H ke bidang ACQ = jarak titik H ke garis OQ.
Perhatikan segitiga ODH siku-siku di D:
$\begin{align} OH &=\sqrt{OD^2+DH^2} \\ &= \sqrt{{\left( \frac{1}{2}a\sqrt{2} \right)}^2+a^2} \\ &= \sqrt{\frac{2}{4}a^2+a^2} \\ &= \sqrt{\frac{6}{4}a^2} \\ OH &= \frac{1}{2}a\sqrt{6} \end{align}$
Perhatikan segitiga OBQ siku-siku di B:
$\begin{align} OQ &=\sqrt{OB^2+BQ^2} \\ & =\sqrt{{\left( \frac{1}{2}a\sqrt{2} \right)}^2+{\left( \frac{1}{2}a \right)}^2} \\ & =\sqrt{\frac{2}{4}a^2+\frac{1}{4}a^2} \\ & =\sqrt{\frac{3}{4}a^2} \\ OQ &=\frac{1}{2}a\sqrt{3} \end{align}$
Perhatikan segitiga HFQ siku-siku di F:
$\begin{align} HQ &=\sqrt{HF^2+FQ^2} \\ & =\sqrt{{\left( a\sqrt{2} \right)}^2+{\left( \frac{1}{2}a \right)}^2} \\ & =\sqrt{2a^2+\frac{1}{4}a^2} \\ & =\sqrt{\frac{9}{4}a^2} \\ HQ &=\frac{1}{2}a\sqrt{9} \end{align}$
Perhatikan segitiga HOQ, ternyata ukuran ketiga sisinya membentuk tripel pythagoras.
$\begin{align} HQ^2 &= OH^2+OQ^2 \\ {\left( \frac{1}{2}a\sqrt{9} \right)}^2 &= {\left( \frac{1}{2}a\sqrt{6} \right)}^2+{\left( \frac{1}{2}a\sqrt{3} \right)}^2 \\ \frac{9}{4}a^2 &= \frac{6}{4}a^2+\frac{3}{4}a^2 \\ \frac{9}{4}a^2 &= \frac{9}{4}a^2 \end{align}$
Maka diperoleh: $OH\bot OQ$
Jadi, Jarak titik H ke bidagn ACQ = jarak titik H ke garis OQ = panjang ruas garis OH yaitu $\frac{1}{2}a\sqrt{6}$.

No. 2 (Latihan 1.3 Matematika Wajib kelas 12)

Suatu kepanitiaan membuat papan nama dari kertas yang membentuk bangun seperti berikut.

Ternyata ABE membentuk segitiga sama sisi, panjang BF = 13 cm dan BC = 12 cm. Tentukan jarak antara titik A dan bidang BCFE.
Pembahasan:

Berdasarkan gambar. Jarak titik A ke BCFE = jarak titik A ke garis EB = panjang ruas garis AP.
Perhatikan segitiga BEF siku-siku di E:
EF = BC = 12 cm
$\begin{align} BE &= \sqrt{BF^2-EF^2} \\ &= \sqrt{13^2-12^2} \\ BE &= 5 \end{align}$
Perhatikan segitiga ABE adalah segitiga sama sisi.
AB = BE = AE = 5 cm.
Garis tinggi AP membagi dua sama panjang sisi BE, maka:
$BP=\frac{1}{2}.BE=\frac{5}{2}$
$\begin{align} AP &= \sqrt{AB^2-BP^2} \\ &= \sqrt{5^2-{\left( \frac{5}{2} \right)}^2} \\ &= \sqrt{25-\frac{25}{4}} \\ &= \sqrt{\frac{75}{4}} \\ AP &= \frac{5}{2}\sqrt{3} \end{align}$
Jadi, jarak titik A ke bidang BCFE adalah $\frac{5}{2}\sqrt{3}$.

No. 3 (Latihan 1.3 Matematika Wajib kelas 12)

Dari gambar di bawah, jika diketahui panjang AB = 8 cm, BC = 6 cm dan EC = $5\sqrt{5}$. Tentukan jarak antara titik B dan bidang ACE.

Pembahasan:
Jarak titik B ke bidang ACE = jarak titik B ke bidang ACGE = jarak titik B ke garis AC = panjang ruas garis BQ.
Perhatikan segitiga ABC:

$\begin{align} AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{8^2+6^2} \\ AB &= 10 \end{align}$
Dengan menggunakan luas ABC, maka:
$\begin{align} \frac{1}{2}.AC.BQ &=\frac{1}{2}.AB.BC \\ AC.BQ &= AB.BC \\ 10.BQ &= 8.6 \\ BQ &= \frac{48}{10} \\ BQ &= \frac{24}{5} \end{align}$
Jadi, jarak titik B ke bidang ACE adalah $\frac{24}{5}$

No. 4 (Latihan 1.3 Matematika Wajib kelas 12)

Diketahui limas segitiga beraturan T.ABC. Panjang AB = 6 cm dan TA = 8 cm. Tentukan jarak antara titik T dengan bidang ABC.
Pembahasan:

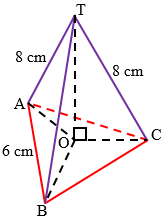
Jarak titik T ke bidang ABC adalah panjang garis tinggi limas yaitu TO.
Perhatikan alas limas T.ABC berbentuk segitiga sama sisi.

Perhatikan segitiga ODC siku-siku di D:
$\angle OAD=30^o$
$\begin{align} \cos \angle OCD &=\frac{CD}{OC} \\ \cos {30^o} &= \frac{3}{OC} \\ \frac{1}{2}\sqrt{3} &= \frac{\sqrt{3}.\sqrt{3}}{OC} \\ OC &= 2\sqrt{3}
\end{align}$
Perhatikan segitiga TOC siku-siku di O:
$\begin{align} TO &= \sqrt{TC^2-OC^2} \\ &= \sqrt{8^2-{\left( 2\sqrt{3} \right)}^2} \\ &= \sqrt{64-12} \\ &= \sqrt{52} \\ TO &= 2\sqrt{13} \end{align}$
Jadi, jarak titik T ke bidang ABC adalah $2\sqrt{13}$.

No. 5 (Latihan 1.3 Matematika Wajib kelas 12)

Diketahui luas permukaan kubus ABCD.EFGH adalah 294 $cm^2$. Tentukan:
a. Jarak antara titik F ke bidang ADHE
b. Jarak antara titik B ke bidang ACH.
Pembahasan:
L = 294
$\begin{align} L &= 294 \\ 6s^2 &= 294 \\ s^2 &= 49 \\ s &=7 \end{align}$
Jadi, rusuk kubus ABCD.EFGH adalah 7 cm.
a. Jarak titik F ke bidang ADHE

Dari gambar jarak titik F ke bidang ADHE = jarak titik F ke titik E = panjang ruas garis EF = 7 cm.

b. Jarak titik B ke bidang ACH.
Bidang ACH dapat diperluas dengan cara:
Perpanjang garis HA, sehingga diperoleh garis HP
Perpanjang garis HC, sehingga diperoleh garis HR
Perpanjang garis FB, sehingga diperoleh garis FQ
Maka kita peroleh perluasan bidang ACH menjadi bidang HPR
Untuk jelasnya, perhatikan gambar berikut

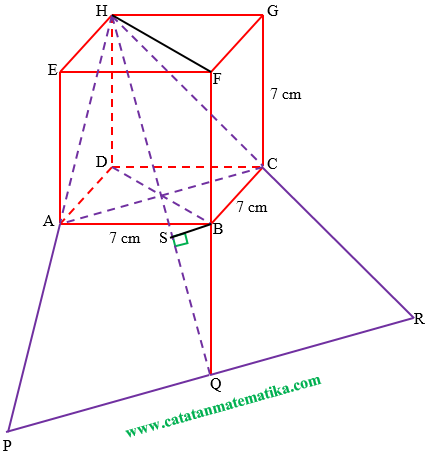
Jarak titik B ke bidang ACH = jarak titik B ke bidang HPR = jarak titik B ke garis HQ = panjang ruas garis BS.
Untuk menghitung panjang ruas garis BS perhatikan segitiga HFQ siku-siku di F:

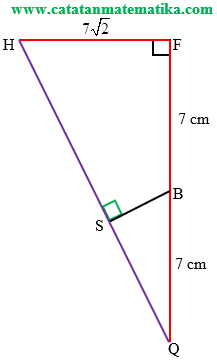
$\begin{align} HQ &= \sqrt{FQ^2+FH^2} \\ &= \sqrt{{14}^2+{\left( 7\sqrt{2} \right)}^2} \\ &= \sqrt{196+98} \\ &= \sqrt{294} \\ HQ &=7\sqrt{6} \end{align}$
Segitiga HFQ sebangun dengan segitiga BSQ, maka diperoleh perbandingan sisi-sisi yang bersesuaian sebagai berikut:
$\begin{align} \frac{BS}{FH} &= \frac{BQ}{HQ} \\ \frac{BS}{7\sqrt{2}} &= \frac{7}{7\sqrt{6}} \\ BS &= \frac{7}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ BS &= \frac{7}{3}\sqrt{3} \end{align}$
Jadi, jarak titik B ke bidang ACH adalah $\frac{7}{3}\sqrt{3}$.

C. Soal Latihan

1. Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Jarak titik E ke bidang BDG adalah … cm.
2. Pada kubus ABCD.EFGH panjang rusuknya 12 cm. Titik Q adalah titik tengah rusuk BF. Jarak titik H ke bidang ACQ sama dengan … cm.
3. Diketahui kubus ABCD.EFGH dengan rusuk 10 cm. Jarak titik A ke bidang CFH adalah … cm.
4. Diketahui bidang empat T.ABC dengan AT, AB dan AC saling tegak lurus di A. Jika panjang AB = AC = AT = 5 cm, maka jarak titik A ke bidang TBC adalah … cm.
5. Diketahui limas segi empat beraturan T.ABCD dengan panjang rusuk sama yaitu 6 cm. Jika P titik tengah CD, maka jarak titik P ke bidang TAB adalah ... cm.

Semoga postingan: Dimensi Tiga 3. Jarak Titik ke Bidang pada Bangun Ruang ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :