Pembahasan UTUL UGM 2013 Matematika IPA Kode 261
Berikut ini adalah Soal dan Pembahasan Matematika IPA UTUL UGM 2013 Kode 261. Pembahasan ini saya buat untuk membantu adik-adik yang akan mengikuti seleksi tertulis ini diselenggarakan oleh Universitas Gadjah Mada (UGM) untuk menyeleksi mahasiswa baru yang akan masuk UGM pada tahun ajaran 2018-2019. Oh iya, adik-adik perlu mengetahui bahwa kalian yang alumni SMA 2018, 2017, dan 2016 diperbolehkan lho mengikuti seleksi tertulis ini. Dan jangan lupa ya..., pendaftaran terakhir tanggal 25 Juni 2018, dan tes tertulis dilaksanakan pada tanggal 08 Juli 2018. Dengan melihat rentang waktu yang ada, berarti kalian masih memiliki cukup waktu untuk belajar. Yuk... kita pelajari bersama Soal dan Pembahasan Matematika IPA UTUL UGM 2013 Kode 261 berikut ini. Catatan Matematika menyediakan file soal untuk dapat didownload dan diprint.
A. $(3,\sqrt3)$
B. $(3,3\sqrt3)$
C. $(3,2+\sqrt3)$
D. $(3,2+2\sqrt3)$
E. $(3,2+3\sqrt3)$
Pembahasan:
Perhatikan gambar berikut ini.
PR adalah jarak titik P(3,b) terhadap garis $y=-x\sqrt{3}+2$, maka:
$=\left| \frac{{{x}_{1}}.\sqrt{3}+{{y}_{1}}-2}{\sqrt{{{(\sqrt{3})}^{2}}+{{1}^{2}}}} \right|$
$=\left| \frac{3.\sqrt{3}+b-2}{2} \right|$
PQ adalah jarak titik $P(3,b)$ ke titik $Q(3,2)$, maka:
$PQ=b-2$
$PQ=PR=r$
$\begin{align}b-2&=\frac{3\sqrt{3}+b-2}{2} \\ 2b-4&=3\sqrt{3}+b-2 \\ b&=2+3\sqrt{3} \end{align}$
Jadi, titik pusat lingkaran adalah P$(3,2+3\sqrt3)$.
Kunci: E
A. $\frac{1}{4}$ B. $\frac{1}{4}\sqrt{2}$ C. $\frac{1}{4}\sqrt{6}$ D. $\frac{1}{4}\sqrt{7}$ E. $\frac{1}{4}\sqrt{14}$
Pembahasan:
Perhatikan gambar berikut!
Perhatikan segitiga OCB siku-siku di C, berlaku phytagoras
$BC=\sqrt{7}$, $OC=3$, maka:
$OB=\sqrt{B{{C}^{2}}+O{{C}^{2}}}$
$OB=\sqrt{{{(-3)}^{2}}+{{(\sqrt{7})}^{2}}}$
$OB=4$
$\cos (\alpha +\beta )=\frac{OC}{OB}=\frac{3}{4}$
Ingat: $2{{\cos }^{2}}x=1+\cos 2x$, maka:
$2{{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=1+\cos (\alpha +\beta )$
$2{{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=1+\frac{3}{4}$
$2{{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=\frac{7}{4}$
${{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=\frac{7}{8}$
$\cos \frac{1}{2}(\alpha +\beta )=\sqrt{\frac{7}{8}}=\frac{\sqrt{7}}{2\sqrt{2}}.\frac{\sqrt{2}}{\sqrt{2}}=\frac{1}{4}\sqrt{14}$
Kunci: E
A. $\frac{2}{9}\sqrt{2}$ B. $\frac{2}{9}\sqrt{6}$ C. $\frac{2}{3}\sqrt{2}$ D. $\frac{2}{3}\sqrt{6}$ E. 2
Pembahasan:
$\cos \theta =\frac{\vec{u}.\vec{v}}{|\vec{u}||\vec{v}|}$
$\frac{1}{3}=\frac{\left( \begin{matrix} a \\ 1 \\ -a \\ \end{matrix} \right).\left( \begin{matrix} 1 \\ a \\ a \\ \end{matrix} \right)}{\sqrt{{{a}^{2}}+{{1}^{2}}+{{(-a)}^{2}}}.\sqrt{{{1}^{2}}+{{a}^{2}}+{{a}^{2}}}}$
$\frac{1}{3}=\frac{2a-{{a}^{2}}}{\sqrt{2{{a}^{2}}+1}.\sqrt{2{{a}^{2}}+1}}$
$\frac{1}{3}=\frac{2a-{{a}^{2}}}{2{{a}^{2}}+1}$
$2{{a}^{2}}+1=6a-3{{a}^{2}}$
$5{{a}^{2}}-6a+1=0$
$(5a-1)(a-1)=0$,
${{a}_{1}}=\frac{1}{5}$ atau ${{a}_{2}}=1$
Karena soal pilihan berganda, kita uji yang paling sederhana yaitu ${{a}_{2}}=1$.
$\vec{u}=(1,1,-1)$ dan $\vec{v}=(1,1,1)$ maka $u.v=\left( \begin{matrix} 1 \\ 1 \\ -1 \\ \end{matrix} \right).\left( \begin{matrix} 1 \\ 1 \\ 1 \\ \end{matrix} \right)=1$
$|\vec{u}|=|\vec{v}|=\sqrt{2{{a}^{2}}+1}=\sqrt{3}$
$|{{\vec{u}}_{1}}|=\left| \frac{\vec{u}.\vec{v}}{|\vec{v}|} \right|=\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$
$|{{\vec{v}}_{1}}|=\left| \frac{\vec{v}.\vec{u}}{|\vec{u}|} \right|=\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$
Jika $\cos \theta =\frac{1}{3}\Rightarrow \sin \theta =\frac{2}{3}\sqrt{2}$
Luas jajaran genjang:
$=2.\frac{1}{2}.|{{u}_{1}}|.|{{v}_{1}}|.\sin \theta $
$=2.\frac{1}{2}.\frac{1}{3}\sqrt{3}.\frac{1}{3}\sqrt{3}.\frac{2}{3}\sqrt{2}$
$=\frac{2}{9}\sqrt{2}$
Kunci: A
A. 108 B. 80 C. 72 D. 60 E. 36
Pembahasan:
Perhatikan gambar berikut ini!
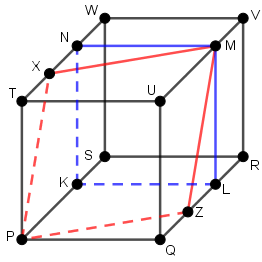
${{V}_{Kubus}}={{6}^{3}}=216$
Jika kita perhatikan gambar! Maka bidang PXYZ membagi volume bangun ruang PQLK.TUMN, maka:
${{V}_{TUYX.PQZ}}=\frac{1}{2}.{{V}_{PQLK.TUMN}}$
${{V}_{TUYX.PQZ}}=\frac{1}{2}.\frac{2}{3}.{{V}_{Kubus}}$
${{V}_{TUYX.PQZ}}=\frac{1}{3}.216=72$
Kunci: C
A. 2 B. $\sqrt{6}$ C. $\sqrt{8}$ D. 3 E. 4
Pembahasan:
Perhatikan gambar berikut ini!
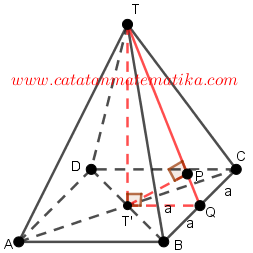
$TT'=2\sqrt{3}$
Perhatikan segitiga $TT'Q$, maka:
$TQ=\sqrt{{{a}^{2}}+{{(2\sqrt{3})}^{2}}}=\sqrt{{{a}^{2}}+12}$
$T'P.TQ=TT'.T'Q$
$T'P=\frac{TT'.T'Q}{TQ}$
$T'P=\frac{2a\sqrt{3}}{\sqrt{{{a}^{2}}+12}}$
Karena P adalah titik berat segitiga TBC, maka:
$PQ=\frac{1}{3}TQ\Leftrightarrow PQ=\frac{1}{3}\sqrt{{{a}^{2}}+12}$
Perhatikan segitiga T’PQ.
$T'{{Q}^{2}}=T'{{P}^{2}}+P{{Q}^{2}}$
${{a}^{2}}={{\left( \frac{2a\sqrt{3}}{\sqrt{{{a}^{2}}+12}} \right)}^{2}}+{{\left( \frac{1}{3}\sqrt{{{a}^{2}}+12} \right)}^{2}}$
${{a}^{2}}=\frac{12{{a}^{2}}}{{{a}^{2}}+12}+\frac{{{a}^{2}}+12}{9}$
$9{{a}^{2}}({{a}^{2}}+12)=108{{a}^{2}}+{{({{a}^{2}}+12)}^{2}}$
$9{{a}^{4}}+108{{a}^{2}}=108{{a}^{2}}+{{a}^{4}}+24{{a}^{2}}+144$
$8{{a}^{4}}-24{{a}^{2}}-144=0$
${{a}^{4}}-3{{a}^{2}}-18=0$
$({{a}^{2}}+3)({{a}^{2}}-6)=0$
$({{a}^{2}}+3)(a+\sqrt{6})(a-\sqrt{6})=0$
$a=\sqrt{6}$
Jadi, sisi alas limas $=2a=2\sqrt{6}$
Kunci: Tidak Ada Opsi
A. $3x+9y+11=0$
B. $3x+9y-11=0$
C. $-3x+9y+11=0$
D. $-3x+9y-11=0$
E. $3x-9y-11=0$
Pembahasan:
Kurva $y=2{{x}^{2}}-x-1$ maka ${{m}_{g}}=y'=4x-1$
Misal garis k: $2x-y+4=0$, ${{m}_{k}}=2$, $\angle ({{m}_{g}},{{m}_{k}})={{45}^{o}}$, maka:
$tg{{45}^{o}}=\left| \frac{{{m}_{g}}-{{m}_{k}}}{1+{{m}_{g}}.{{m}_{k}}} \right|$
$1=\left| \frac{{{m}_{g}}-2}{1+{{m}_{g}}.2} \right|$, diketahui pada soal $0 < m_g < 2$, maka:
$1+2{{m}_{g}}=-{{m}_{g}}+2$
$3{{m}_{g}}=1$
${{m}_{g}}=\frac{1}{3}$
$4x-1=\frac{1}{3}$
$12x-3=1\Leftrightarrow {{x}_{1}}=\frac{1}{3}$
$y=2{{x}^{2}}-x-1$
${{y}_{1}}=2{{\left( \frac{1}{3} \right)}^{2}}-\frac{1}{3}-1=\frac{-10}{9}$
Garis g melalui titik $\left( \frac{1}{3},\frac{-10}{9} \right)$ dan $m=\frac{1}{3}$ adalah:
$y-{{y}_{1}}=m(x-{{x}_{1}})$
$y+\frac{10}{9}=\frac{1}{3}(x-\frac{1}{3})$
$3x-9y-11=0$ atau $-3x+9y+11=0$
Kunci: C/E
A. $x > -\frac{8}{3}$ B. $x < -\frac{8}{3}$ C. $x < -\frac{8}{7}$ D. $x > -\frac{8}{7}$ E. $x < -\frac{12}{5}$
Pembahasan:
$\sqrt{{{625}^{x-2}}} > \sqrt{{{125}^{x}}}.\sqrt[3]{{{25}^{6x}}}$
${{\left( {{5}^{4}} \right)}^{\frac{x-2}{2}}} > {{\left( {{5}^{3}} \right)}^{\frac{x}{2}}}.{{\left( {{5}^{2}} \right)}^{\frac{6x}{3}}}$
${{5}^{2x-4}} > {{5}^{\frac{3x}{2}+4x}}$
$2x-4 > \frac{3x}{2}+4x$
$4x-8 > 3x+8x$
$x < -\frac{8}{7}$
Kunci: C
A. $\{x|0\le x\le \frac{7}{2}\}$
B. $\{x|x\ge 0\}$
C. $\{x|x\le \frac{1}{2}\}$
D. $\{x|0\le x\le \frac{5}{2}\}$
E. $\{x|-1\le x\le \frac{1}{2}\}$
Pembahasan:
$|x-2|-1\ge x$
$|x-2|\ge x+1$
Untuk $x\ge 2$ maka:
$|x-2|-1\ge x$
$x-2\ge x+1\Leftrightarrow -2\ge 1$
$-2\ge 1$, tidak ada penyelesaian.
Untuk $x < 2$ maka:
$|x-2|-1\ge x$
$-(x-2)\ge x+1$
$-2x\ge -1$
$x\le \frac{1}{2}$
Kunci: C
A. $-11x-10$
B. $-10x-11$
C. $11x-10$
D. $10x+11$
E. $11x+10$
Pembahasan:
Yang dibagi = pembagi x hasil + sisa
$Q(x)=(x+2).Hasil+3$
$Q(-2)=(-2+2).Hasil+3=3$
$P(x)=({{x}^{2}}-x-2).Q(x)+x+2$
$P(x)=(x-2)(x+1).Q(x)+x+2$
Untuk x = -2, maka:
$P(-2)=(-2-2)(-2+1).Q(-2)+(-2)+2$
$P(-2)=-4.(-1).3-2+2=12$
Untuk x = -1, maka:
$P(-1)=(-1-2)(-1+1).Q(-1)+(-1)+2$
$P(-1)=1$
Pertanyaan:
$P(x)=({{x}^{2}}+3x+2).Hasil+ax+b$
$P(x)=(x+2)(x+1).Hasil+ax+b$
$P(-2)=-2a+b=12$
$P(-1)=-a+b=1$
---------------------------- (-)
$-a=11\Leftrightarrow a=-11,b=-10$
Jadi, sisa $ax+b=-11x-10$
Kunci: A
A. 2 B. 4 C. 6 D. 8 E. 10
Pembahasan:
Barisan aritmetika: ${{S}_{4}}=2(2a+3b)$, ${{S}_{8}}=4(2a+7b)$, $8(2a+15b)$
Barisan geometri: ${{S}_{4}}$, ${{S}_{8}}$ dan ${{S}_{16}}$
${{({{S}_{8}})}^{2}}={{S}_{4}}.{{S}_{6}}$
${{[4(2a+7b)]}^{2}}=[2(2a+3b)][8(2a+15b)]$
$16(4{{a}^{2}}+28ab+49{{b}^{2}})=16(4{{a}^{2}}+36ab+45{{b}^{2}})$
$4{{a}^{2}}+28ab+49{{b}^{2}}=4{{a}^{2}}+36ab+45{{b}^{2}}$
$4{{b}^{2}}-8ab=0$
$4b(b-2a)=0$ maka $b=0$ atau $b=2a$
$b=0$ maka $\frac{{{S}_{8}}}{{{S}_{4}}}=\frac{4(2a+7.0)}{2(2a+3.0)}=\frac{8a}{4a}=2$
$b=2a$ maka $\frac{{{S}_{8}}}{{{S}_{4}}}=\frac{4(2a+7.2a)}{2(2a+3.2a)}=\frac{64a}{16a}=4$
Kunci: A dan B
A. 0 B. $\frac{1}{2}$ C. $\frac{3}{4}$ D. $\frac{3}{2}$ E. 3
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{\cos }^{3}}x}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{(1-\cos x)(1+\cos x+{{\cos }^{2}}x)}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{2{{\sin }^{2}}\frac{1}{2}x.(1+\cos x+{{\cos }^{2}}x)}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{2\sin \frac{1}{2}x.\sin \frac{1}{2}x}{x\tan x}(1+\cos x+{{\cos }^{2}}x)$
$=2.\frac{1}{2}.\frac{1}{2}.(1+1+1)$
$=\frac{3}{2}$
Kunci: D
A. {$x|x\le 0$ atau $x\ge 2$}
B. {$x|x\le 0$ atau $x\ge 1$}
C. {$x|x\le -2$ atau $x\ge 0$}
D. {$x|x\le -\frac{1}{2}$ atau $x\ge 0$}
E. {$x|x\le -2$ atau $x\ge 1$}
Pembahasan:
$f(x)=a{{x}^{3}}-b{{x}^{2}}+1$
$f(1)=a-b+1=-5$
$a-b=-6$
$a=b-6$
Titik ekstrim di $(1,-5)$, maka $f'(1)=0$
$f'(x)=3a{{x}^{2}}-2bx$
$f'(1)=3a-2b=0$
$3a-2b=0$
$3(b-6)-2b=0$
$b=18$
$a=b-6\Leftrightarrow a=18-6=12$
Kurva naik untuk $f'(1)\ge 0$
$3a{{x}^{2}}-2bx\ge 0$
$3.12{{x}^{2}}-2.18x\ge 0$
$36{{x}^{2}}-36x\ge 0$
$36x(x-1)\ge 0$
$x=0$ atau $x=1$
HP = {$x|x\le 0$ atau $x\ge 1$}
Kunci: B
A. 13 B. 11 C. 9 D. 5 E. 3
Pembahasan:
Misal:
p = jumlah anak laki-laki
w = jumlah anak perempuan
p + w = 15, w = 15 – p
$C_{1}^{p}.C_{1}^{w}=26$
$p.w=26$
$p(15-p)=26$
$15p-{{p}^{2}}=26$
${{p}^{2}}-15p+26=0$
$(p-13)(p-2)=0$
$p=13$ atau $p=2$
$w=15-p$
$p=13\Rightarrow w=2\Rightarrow p-w=11$
$p=2\Rightarrow w=13\Rightarrow w-p=11$
Kunci: B
A. -2 B. -1 C. 0 D. 1 E. 2
Pembahasan:
$f(x)$ habis dibagi $x-1$ maka $f(1)=0$
$f'(x)$ dibagi $x-1$ bersisa $f'(1)={{a}^{2}}$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=2a-1$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{f'(x)}{1}=2a-1$
$f'(1)=2a-1$
${{a}^{2}}=2a-1$
${{a}^{2}}-2a+1=0$
$(a-1)(a-1)=0$
$a=1$
Kunci: D
A. $\frac{\pi }{2}$ B. $\frac{\pi }{4}$ C. $\frac{\pi }{6}$ D. $\frac{\pi }{24}$ E. $\frac{\pi }{36}$
Pembahasan:
1 = ${}^{2}\log 16$ + ${}^{2}\log (\sin x)$ + ${}^{2}\log (\cos x)$ + ${}^{2}\log (\cos 2x)$
$1={}^{2}\log 16.\sin x.\cos x.\cos 2x$
$2=16.\sin x.\cos x.\cos 2x$
$2=8.2\sin x.\cos x.\cos 2x$
$2=8\sin 2x.\cos 2x$
$2=4.2\sin 2x.\cos 2x$
$2=4\sin 4x$
$\sin 4x=\frac{1}{2}$
$\sin 4x=\sin \frac{\pi }{6}\Leftrightarrow 4x=\frac{\pi }{6}\Leftrightarrow x=\frac{\pi }{24}$
Kunci: D
Matematika IPA UTUL UGM 2013 Kode 261 No. 1
Titik pusat lingkaran yang menyinggung garis $y=2$ di $(3,2)$ dan menyinggung garis $y=-x\sqrt3+2$ adalah ...A. $(3,\sqrt3)$
B. $(3,3\sqrt3)$
C. $(3,2+\sqrt3)$
D. $(3,2+2\sqrt3)$
E. $(3,2+3\sqrt3)$
Pembahasan:
Perhatikan gambar berikut ini.
PR adalah jarak titik P(3,b) terhadap garis $y=-x\sqrt{3}+2$, maka:
$=\left| \frac{{{x}_{1}}.\sqrt{3}+{{y}_{1}}-2}{\sqrt{{{(\sqrt{3})}^{2}}+{{1}^{2}}}} \right|$
$=\left| \frac{3.\sqrt{3}+b-2}{2} \right|$
PQ adalah jarak titik $P(3,b)$ ke titik $Q(3,2)$, maka:
$PQ=b-2$
$PQ=PR=r$
$\begin{align}b-2&=\frac{3\sqrt{3}+b-2}{2} \\ 2b-4&=3\sqrt{3}+b-2 \\ b&=2+3\sqrt{3} \end{align}$
Jadi, titik pusat lingkaran adalah P$(3,2+3\sqrt3)$.
Kunci: E
Matematika IPA UM –UGM 2013 Kode 261 No. 2
Diberikan koordinat titik $O(0,0)$, $B(-3,\sqrt7)$, dan $A(a,0)$, dengan $a < 0$. Jika pada segitiga AOB, $\angle OAB=\alpha $ dan $\angle OBA=\beta $, maka $\cos \frac{1}{2}(\alpha +\beta )$ = … A. $\frac{1}{4}$ B. $\frac{1}{4}\sqrt{2}$ C. $\frac{1}{4}\sqrt{6}$ D. $\frac{1}{4}\sqrt{7}$ E. $\frac{1}{4}\sqrt{14}$
Pembahasan:
Perhatikan gambar berikut!
Perhatikan segitiga OCB siku-siku di C, berlaku phytagoras
$BC=\sqrt{7}$, $OC=3$, maka:
$OB=\sqrt{B{{C}^{2}}+O{{C}^{2}}}$
$OB=\sqrt{{{(-3)}^{2}}+{{(\sqrt{7})}^{2}}}$
$OB=4$
$\cos (\alpha +\beta )=\frac{OC}{OB}=\frac{3}{4}$
Ingat: $2{{\cos }^{2}}x=1+\cos 2x$, maka:
$2{{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=1+\cos (\alpha +\beta )$
$2{{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=1+\frac{3}{4}$
$2{{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=\frac{7}{4}$
${{\cos }^{2}}\frac{1}{2}(\alpha +\beta )=\frac{7}{8}$
$\cos \frac{1}{2}(\alpha +\beta )=\sqrt{\frac{7}{8}}=\frac{\sqrt{7}}{2\sqrt{2}}.\frac{\sqrt{2}}{\sqrt{2}}=\frac{1}{4}\sqrt{14}$
Kunci: E
Matematika IPA UTUL UGM 2013 Kode 261 No. 3
Diketahui vektor-vektor $\vec{u}=(a,1,-a)$ dan $\vec{v}=(1,a,a)$. Jika ${{\vec{u}}_{1}}$ vektor proyeksi $\vec{u}$ pada $\vec{v}$, ${{\vec{v}}_{1}}$ vektor proyeksi $\vec{v}$ pada $\vec{u}$, dan $\theta $ sudut antara $\vec{u}$ dan $\vec{v}$ dengan $\cos \theta =\frac{1}{3}$, maka luas jajaran genjang yang dibentuk oleh ${{\vec{u}}_{1}}$ dan ${{\vec{v}}_{1}}$ adalah ….A. $\frac{2}{9}\sqrt{2}$ B. $\frac{2}{9}\sqrt{6}$ C. $\frac{2}{3}\sqrt{2}$ D. $\frac{2}{3}\sqrt{6}$ E. 2
Pembahasan:
$\cos \theta =\frac{\vec{u}.\vec{v}}{|\vec{u}||\vec{v}|}$
$\frac{1}{3}=\frac{\left( \begin{matrix} a \\ 1 \\ -a \\ \end{matrix} \right).\left( \begin{matrix} 1 \\ a \\ a \\ \end{matrix} \right)}{\sqrt{{{a}^{2}}+{{1}^{2}}+{{(-a)}^{2}}}.\sqrt{{{1}^{2}}+{{a}^{2}}+{{a}^{2}}}}$
$\frac{1}{3}=\frac{2a-{{a}^{2}}}{\sqrt{2{{a}^{2}}+1}.\sqrt{2{{a}^{2}}+1}}$
$\frac{1}{3}=\frac{2a-{{a}^{2}}}{2{{a}^{2}}+1}$
$2{{a}^{2}}+1=6a-3{{a}^{2}}$
$5{{a}^{2}}-6a+1=0$
$(5a-1)(a-1)=0$,
${{a}_{1}}=\frac{1}{5}$ atau ${{a}_{2}}=1$
Karena soal pilihan berganda, kita uji yang paling sederhana yaitu ${{a}_{2}}=1$.
$\vec{u}=(1,1,-1)$ dan $\vec{v}=(1,1,1)$ maka $u.v=\left( \begin{matrix} 1 \\ 1 \\ -1 \\ \end{matrix} \right).\left( \begin{matrix} 1 \\ 1 \\ 1 \\ \end{matrix} \right)=1$
$|\vec{u}|=|\vec{v}|=\sqrt{2{{a}^{2}}+1}=\sqrt{3}$
$|{{\vec{u}}_{1}}|=\left| \frac{\vec{u}.\vec{v}}{|\vec{v}|} \right|=\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$
$|{{\vec{v}}_{1}}|=\left| \frac{\vec{v}.\vec{u}}{|\vec{u}|} \right|=\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$
Jika $\cos \theta =\frac{1}{3}\Rightarrow \sin \theta =\frac{2}{3}\sqrt{2}$
Luas jajaran genjang:
$=2.\frac{1}{2}.|{{u}_{1}}|.|{{v}_{1}}|.\sin \theta $
$=2.\frac{1}{2}.\frac{1}{3}\sqrt{3}.\frac{1}{3}\sqrt{3}.\frac{2}{3}\sqrt{2}$
$=\frac{2}{9}\sqrt{2}$
Kunci: A
Matematika IPA UTUL UGM 2013 Kode 261 No. 4
Panjang rusuk kubus PQRS.TUVW adalah 6 cm. Titik X, pada TW, Y pada UV dan Z pada QR. Jika $|TX|:|XW|=1:2$, $|UY|:|YV|=2:1$, dan $PXYZ$ membentuk bidang datar, maka volume bangun $TUYX.PQZ$ adalah … $c{{m}^{3}}$A. 108 B. 80 C. 72 D. 60 E. 36
Pembahasan:
Perhatikan gambar berikut ini!
${{V}_{Kubus}}={{6}^{3}}=216$
Jika kita perhatikan gambar! Maka bidang PXYZ membagi volume bangun ruang PQLK.TUMN, maka:
${{V}_{TUYX.PQZ}}=\frac{1}{2}.{{V}_{PQLK.TUMN}}$
${{V}_{TUYX.PQZ}}=\frac{1}{2}.\frac{2}{3}.{{V}_{Kubus}}$
${{V}_{TUYX.PQZ}}=\frac{1}{3}.216=72$
Kunci: C
Matematika IPA UTUL UGM 2013 Kode 261 No. 5
Diketahui limas beraturan T.ABCD dengan alas berbentuk persegi dan tinggi limas $2\sqrt{3}$ cm. Jika T’ proyeksi T pada bidang alas dan titik P adalah perpotongan garis berat segitiga TBC, maka panjang sisi alas limas agar T’P tegak lurus segitiga TBC adalah … cm.A. 2 B. $\sqrt{6}$ C. $\sqrt{8}$ D. 3 E. 4
Pembahasan:
Perhatikan gambar berikut ini!
$TT'=2\sqrt{3}$
Perhatikan segitiga $TT'Q$, maka:
$TQ=\sqrt{{{a}^{2}}+{{(2\sqrt{3})}^{2}}}=\sqrt{{{a}^{2}}+12}$
$T'P.TQ=TT'.T'Q$
$T'P=\frac{TT'.T'Q}{TQ}$
$T'P=\frac{2a\sqrt{3}}{\sqrt{{{a}^{2}}+12}}$
Karena P adalah titik berat segitiga TBC, maka:
$PQ=\frac{1}{3}TQ\Leftrightarrow PQ=\frac{1}{3}\sqrt{{{a}^{2}}+12}$
Perhatikan segitiga T’PQ.
$T'{{Q}^{2}}=T'{{P}^{2}}+P{{Q}^{2}}$
${{a}^{2}}={{\left( \frac{2a\sqrt{3}}{\sqrt{{{a}^{2}}+12}} \right)}^{2}}+{{\left( \frac{1}{3}\sqrt{{{a}^{2}}+12} \right)}^{2}}$
${{a}^{2}}=\frac{12{{a}^{2}}}{{{a}^{2}}+12}+\frac{{{a}^{2}}+12}{9}$
$9{{a}^{2}}({{a}^{2}}+12)=108{{a}^{2}}+{{({{a}^{2}}+12)}^{2}}$
$9{{a}^{4}}+108{{a}^{2}}=108{{a}^{2}}+{{a}^{4}}+24{{a}^{2}}+144$
$8{{a}^{4}}-24{{a}^{2}}-144=0$
${{a}^{4}}-3{{a}^{2}}-18=0$
$({{a}^{2}}+3)({{a}^{2}}-6)=0$
$({{a}^{2}}+3)(a+\sqrt{6})(a-\sqrt{6})=0$
$a=\sqrt{6}$
Jadi, sisi alas limas $=2a=2\sqrt{6}$
Kunci: Tidak Ada Opsi
Matematika IPA UTUL UGM 2013 Kode 261 No. 6
Garis $g$ merupakan garis singgung kurva $y=2{{x}^{2}}-x-1$ dengan gradien $m$. Jika garis $g$ membentuk sudut ${{45}^{o}}$ terhadap garis $2x-y+4=0$, dan $0 < m < 2$, maka persamaan $g$ adalah …A. $3x+9y+11=0$
B. $3x+9y-11=0$
C. $-3x+9y+11=0$
D. $-3x+9y-11=0$
E. $3x-9y-11=0$
Pembahasan:
Kurva $y=2{{x}^{2}}-x-1$ maka ${{m}_{g}}=y'=4x-1$
Misal garis k: $2x-y+4=0$, ${{m}_{k}}=2$, $\angle ({{m}_{g}},{{m}_{k}})={{45}^{o}}$, maka:
$tg{{45}^{o}}=\left| \frac{{{m}_{g}}-{{m}_{k}}}{1+{{m}_{g}}.{{m}_{k}}} \right|$
$1=\left| \frac{{{m}_{g}}-2}{1+{{m}_{g}}.2} \right|$, diketahui pada soal $0 < m_g < 2$, maka:
$1+2{{m}_{g}}=-{{m}_{g}}+2$
$3{{m}_{g}}=1$
${{m}_{g}}=\frac{1}{3}$
$4x-1=\frac{1}{3}$
$12x-3=1\Leftrightarrow {{x}_{1}}=\frac{1}{3}$
$y=2{{x}^{2}}-x-1$
${{y}_{1}}=2{{\left( \frac{1}{3} \right)}^{2}}-\frac{1}{3}-1=\frac{-10}{9}$
Garis g melalui titik $\left( \frac{1}{3},\frac{-10}{9} \right)$ dan $m=\frac{1}{3}$ adalah:
$y-{{y}_{1}}=m(x-{{x}_{1}})$
$y+\frac{10}{9}=\frac{1}{3}(x-\frac{1}{3})$
$3x-9y-11=0$ atau $-3x+9y+11=0$
Kunci: C/E
Matematika IPA UTUL UGM 2013 Kode 261 No. 7
Nilai $x$ yang memenuhi pertidaksamaan $\sqrt{{{625}^{x-2}}}>\sqrt{{{125}^{x}}}.\sqrt[3]{{{25}^{6x}}}$ adalah …A. $x > -\frac{8}{3}$ B. $x < -\frac{8}{3}$ C. $x < -\frac{8}{7}$ D. $x > -\frac{8}{7}$ E. $x < -\frac{12}{5}$
Pembahasan:
$\sqrt{{{625}^{x-2}}} > \sqrt{{{125}^{x}}}.\sqrt[3]{{{25}^{6x}}}$
${{\left( {{5}^{4}} \right)}^{\frac{x-2}{2}}} > {{\left( {{5}^{3}} \right)}^{\frac{x}{2}}}.{{\left( {{5}^{2}} \right)}^{\frac{6x}{3}}}$
${{5}^{2x-4}} > {{5}^{\frac{3x}{2}+4x}}$
$2x-4 > \frac{3x}{2}+4x$
$4x-8 > 3x+8x$
$x < -\frac{8}{7}$
Kunci: C
Matematika IPA UTUL UGM 2013 Kode 261 No. 8
Himpunan semua $x$ yang memenuhi $|x-2|-1\ge x$ adalah …A. $\{x|0\le x\le \frac{7}{2}\}$
B. $\{x|x\ge 0\}$
C. $\{x|x\le \frac{1}{2}\}$
D. $\{x|0\le x\le \frac{5}{2}\}$
E. $\{x|-1\le x\le \frac{1}{2}\}$
Pembahasan:
$|x-2|-1\ge x$
$|x-2|\ge x+1$
Untuk $x\ge 2$ maka:
$|x-2|-1\ge x$
$x-2\ge x+1\Leftrightarrow -2\ge 1$
$-2\ge 1$, tidak ada penyelesaian.
Untuk $x < 2$ maka:
$|x-2|-1\ge x$
$-(x-2)\ge x+1$
$-2x\ge -1$
$x\le \frac{1}{2}$
Kunci: C
Matematika IPA UTUL UGM 2013 Kode 261 No. 9
Suku banyak P(x) dibagi ${{x}^{2}}-x-2$ mempunyai hasil bagi Q(x) dan sisa $x+2$. Jika $Q(x)$ dibagi $x+2$ mempunyai sisa 3, maka sisa P(x) dibagi ${{x}^{2}}+3x+2$ adalah ….A. $-11x-10$
B. $-10x-11$
C. $11x-10$
D. $10x+11$
E. $11x+10$
Pembahasan:
Yang dibagi = pembagi x hasil + sisa
$Q(x)=(x+2).Hasil+3$
$Q(-2)=(-2+2).Hasil+3=3$
$P(x)=({{x}^{2}}-x-2).Q(x)+x+2$
$P(x)=(x-2)(x+1).Q(x)+x+2$
Untuk x = -2, maka:
$P(-2)=(-2-2)(-2+1).Q(-2)+(-2)+2$
$P(-2)=-4.(-1).3-2+2=12$
Untuk x = -1, maka:
$P(-1)=(-1-2)(-1+1).Q(-1)+(-1)+2$
$P(-1)=1$
Pertanyaan:
$P(x)=({{x}^{2}}+3x+2).Hasil+ax+b$
$P(x)=(x+2)(x+1).Hasil+ax+b$
$P(-2)=-2a+b=12$
$P(-1)=-a+b=1$
---------------------------- (-)
$-a=11\Leftrightarrow a=-11,b=-10$
Jadi, sisa $ax+b=-11x-10$
Kunci: A
Matematika IPA UTUL UGM 2013 Kode 261 No. 10
Jumlah $n$ suku pertama suatu deret aritmetika dinotasikan dengan ${{S}_{n}}$. Jika suku pertama deret tersebut tak nol dan ${{S}_{4}}$, ${{S}_{8}}$ dan ${{S}_{16}}$ membentuk barisan geometri maka $\frac{{{S}_{8}}}{{{S}_{4}}}$ = …A. 2 B. 4 C. 6 D. 8 E. 10
Pembahasan:
Barisan aritmetika: ${{S}_{4}}=2(2a+3b)$, ${{S}_{8}}=4(2a+7b)$, $8(2a+15b)$
Barisan geometri: ${{S}_{4}}$, ${{S}_{8}}$ dan ${{S}_{16}}$
${{({{S}_{8}})}^{2}}={{S}_{4}}.{{S}_{6}}$
${{[4(2a+7b)]}^{2}}=[2(2a+3b)][8(2a+15b)]$
$16(4{{a}^{2}}+28ab+49{{b}^{2}})=16(4{{a}^{2}}+36ab+45{{b}^{2}})$
$4{{a}^{2}}+28ab+49{{b}^{2}}=4{{a}^{2}}+36ab+45{{b}^{2}}$
$4{{b}^{2}}-8ab=0$
$4b(b-2a)=0$ maka $b=0$ atau $b=2a$
$b=0$ maka $\frac{{{S}_{8}}}{{{S}_{4}}}=\frac{4(2a+7.0)}{2(2a+3.0)}=\frac{8a}{4a}=2$
$b=2a$ maka $\frac{{{S}_{8}}}{{{S}_{4}}}=\frac{4(2a+7.2a)}{2(2a+3.2a)}=\frac{64a}{16a}=4$
Kunci: A dan B
Matematika IPA UTUL UGM 2013 Kode 261 No. 11
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{\cos }^{3}}x}{x\tan x}$ = …A. 0 B. $\frac{1}{2}$ C. $\frac{3}{4}$ D. $\frac{3}{2}$ E. 3
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{\cos }^{3}}x}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{(1-\cos x)(1+\cos x+{{\cos }^{2}}x)}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{2{{\sin }^{2}}\frac{1}{2}x.(1+\cos x+{{\cos }^{2}}x)}{x\tan x}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{2\sin \frac{1}{2}x.\sin \frac{1}{2}x}{x\tan x}(1+\cos x+{{\cos }^{2}}x)$
$=2.\frac{1}{2}.\frac{1}{2}.(1+1+1)$
$=\frac{3}{2}$
Kunci: D
Matematika IPA UTUL UGM 2013 Kode 261 No. 12
Jika kurva $f(x)=a{{x}^{3}}-b{{x}^{2}}+1$ mempunyai titik ekstrim $(1,-5)$ maka kurva tersebut naik pada …A. {$x|x\le 0$ atau $x\ge 2$}
B. {$x|x\le 0$ atau $x\ge 1$}
C. {$x|x\le -2$ atau $x\ge 0$}
D. {$x|x\le -\frac{1}{2}$ atau $x\ge 0$}
E. {$x|x\le -2$ atau $x\ge 1$}
Pembahasan:
$f(x)=a{{x}^{3}}-b{{x}^{2}}+1$
$f(1)=a-b+1=-5$
$a-b=-6$
$a=b-6$
Titik ekstrim di $(1,-5)$, maka $f'(1)=0$
$f'(x)=3a{{x}^{2}}-2bx$
$f'(1)=3a-2b=0$
$3a-2b=0$
$3(b-6)-2b=0$
$b=18$
$a=b-6\Leftrightarrow a=18-6=12$
Kurva naik untuk $f'(1)\ge 0$
$3a{{x}^{2}}-2bx\ge 0$
$3.12{{x}^{2}}-2.18x\ge 0$
$36{{x}^{2}}-36x\ge 0$
$36x(x-1)\ge 0$
$x=0$ atau $x=1$
HP = {$x|x\le 0$ atau $x\ge 1$}
Kunci: B
Matematika IPA UTUL UGM 2013 Kode 261 No. 13
Dari 15 anak terdiri atas laki-laki dan perempuan akan diambil 2 anak secara bersamaan. Jika banyak kemungkinan terambil laki-laki dan perempuan adalah 26, maka selisih jumlah laki-laki dan perempuan adalah …A. 13 B. 11 C. 9 D. 5 E. 3
Pembahasan:
Misal:
p = jumlah anak laki-laki
w = jumlah anak perempuan
p + w = 15, w = 15 – p
$C_{1}^{p}.C_{1}^{w}=26$
$p.w=26$
$p(15-p)=26$
$15p-{{p}^{2}}=26$
${{p}^{2}}-15p+26=0$
$(p-13)(p-2)=0$
$p=13$ atau $p=2$
$w=15-p$
$p=13\Rightarrow w=2\Rightarrow p-w=11$
$p=2\Rightarrow w=13\Rightarrow w-p=11$
Kunci: B
Matematika IPA UTUL UGM 2013 Kode 261 No. 14
Diketahui polinomial $f(x)$ habis dibagi $x-1$. Jika $f'(x)$ dibagi $x-1$ bersisa ${{a}^{2}}$ dan $\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=2a-1$ maka $a$ = …A. -2 B. -1 C. 0 D. 1 E. 2
Pembahasan:
$f(x)$ habis dibagi $x-1$ maka $f(1)=0$
$f'(x)$ dibagi $x-1$ bersisa $f'(1)={{a}^{2}}$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=2a-1$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{f'(x)}{1}=2a-1$
$f'(1)=2a-1$
${{a}^{2}}=2a-1$
${{a}^{2}}-2a+1=0$
$(a-1)(a-1)=0$
$a=1$
Kunci: D
Matematika IPA UTUL UGM 2013 Kode 261 No. 15
Jika sudut lancip $x$ memenuhi 1 = ${}^{2}\log 16$ + ${}^{2}\log (\sin x)$ + ${}^{2}\log (\cos x)$ + ${}^{2}\log (\cos 2x)$ maka $x$ = …A. $\frac{\pi }{2}$ B. $\frac{\pi }{4}$ C. $\frac{\pi }{6}$ D. $\frac{\pi }{24}$ E. $\frac{\pi }{36}$
Pembahasan:
1 = ${}^{2}\log 16$ + ${}^{2}\log (\sin x)$ + ${}^{2}\log (\cos x)$ + ${}^{2}\log (\cos 2x)$
$1={}^{2}\log 16.\sin x.\cos x.\cos 2x$
$2=16.\sin x.\cos x.\cos 2x$
$2=8.2\sin x.\cos x.\cos 2x$
$2=8\sin 2x.\cos 2x$
$2=4.2\sin 2x.\cos 2x$
$2=4\sin 4x$
$\sin 4x=\frac{1}{2}$
$\sin 4x=\sin \frac{\pi }{6}\Leftrightarrow 4x=\frac{\pi }{6}\Leftrightarrow x=\frac{\pi }{24}$
Kunci: D
Artikel Terkait:
|
Update Postingan Terbaru dengan cara subscribe atau follow channel kami dengan klik ketiga tombol di bawah ini:
Post a comment for "Pembahasan UTUL UGM 2013 Matematika IPA Kode 261"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.