Pembahasan Matematika Olimpiade Guru SMA 2018 LOSPI (Part-2)
catatanmatematika.com membagikan soal dan pembahasan matematika olimpiade guru SMA 2018 yang di selenggarakan oleh LOSPI di Universitas Sumatera Utara (USU) pada tanggal 25 Februari 2018. Pembahasan ini adalah pembahasan terakhir dan lanjutan dari Pembahasan Matematika Olimpiade Guru SMA 2018 LOSPI (Part-1).
Soal LOSPI Olimpiade Guru No. 16
Himpunan 20 buah bilangan mempunyai rata-rata 20. Sembilan di antara bilangan itu rata-ratanya 9. Rata-rata dari 11 bilangan yang tersisa adalah ...
A. 11 B. 15 C. 25 D. 29 E. 30
Pembahasan:
$n_1 = 9$ dan $\bar{x}_1$
$n_2 = 11$
$\bar{x}_{gabungan} = 20$
$\bar{x}_2 = ...?$
$\begin{align*} \bar{x}_{gabungan} &= \frac{n_1. \bar{x}_1 + n_2. \bar{x}_2}{n_1 + n_2} \\
20 &= \frac{9.9 + 11. \bar{x}_2}{9 + 11} \\
400 &= 81 + 11. \bar{x}_2 \\
319 &= 11. \bar{x}_2 \\
29 &= \bar{x}_2
\end{align*}$
Kunci: D
Soal LOSPI Olimpiade Guru No. 17
Diketahui $p$ adalah sembarang bilangan bulat positif, $2x + p = y$, $p + y = x$, dan $x + y = z$. Tentukan nilai maksimum yang mungkin dari $(x + y + z)$.
A. 10 B. -10 C. 20 D. -20 E. 30
Pembahasan:
Diketahui:
$p > 0$
$2x + p = y$ ...... pers. (1)
$p + y = x$ ........ pers. (2)
$x + y = z$ ........ pers. (3)
Jumlahkan pers. (1) dengan (2), diperoleh:
$2x + 2p + y = x + y$
$x + 2p = 0$
$x = -2p$
$2x + p = y$
$2.(-2p) + p = y$
$-3p = y$
Substitusi ke pers. (3)
x + y = z
-2p - 3p = z
-5p = z
Nilai maksimum (bernilai positif)
= x + y + z
= 2p + 3p + 5p
= 10p
Kunci: A
Soal LOSPI Olimpiade Guru No. 18
Perhatikan gambar berikut ini:
Bila panjang BP = $\sqrt{160}$, tentukan panjang CP.
A. 10 B. 12 C. 13 D. 14 E. 15
Pembahasan:
Dengan Teorema Bendera Inggris (British Flag Teorem):
$\begin{align*} AP^2 + CP^2 &= BP^2 + DP^2 \\
5^2 + CP^2 &= (\sqrt{160})^2 + 3^2 \\
25 + CP^2 &= 160 + 9 \\
CP^2 &= 144 \\
CP^2 &= 12
\end{align*}$
Kunci: B
Soal LOSPI Olimpiade Guru No. 19
Hitunglah: $\frac{(2008-2007)^2 + (2008 + 2007)^2}{2008^2 + 2007^2}$
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
$\frac{(2008-2007)^2 + (2008 + 2007)^2}{2008^2 + 2007^2}$
$= \frac{2008^2 - 2.2008.2007 + 2007^2 + 2008^2 + 2.200.2007 + 2007^2}{2008^2 + 2007^2}$
$= \frac{2(2008^2 + 2007^2)}{2008^2 + 2007^2}$
=2
Kunci: B
Soal LOSPI Olimpiade Guru No. 20
Hitunglah: $\frac{657 \times 657 \times 657 - 368 \times 368 \times 368}{657 \times 657 + 657 \ times 368 + 368 \times 368}$
A. 273 B. 285 C. 289 D. 290 E. 292
Pembahasan:
Ingat: $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$
$\begin{align*} &\frac{657 \times 657 \times 657 - 368 \times 368 \times 368}{657 \times 657 + 657 \times 368 + 368 \times 368} \\
&= \frac{657^3 - 368^3}{657^2 + 657 \times 368 + 368^2} \\
&= \frac{(657 - 368)(657^2 + 657 \times 368 + 368^2)}{657^2 + 657 \times 368 + 368^2} \\
&= 657 - 368 \\
&= 289
\end{align*}$
Kunci: C
Soal LOSPI Olimpiade Guru No. 21
Perhatikan gambar!
Segitiga ABC adalah segitiga sama kaki dengan AB = BC dan BC = 30 cm. Persegi EFGH mempunyai panjang sisi 12 cm, maka luas segitiga AEF adalah ... cm$^2$.
A. 48 B. 49 C. 50 D. 51 E. 53
Pembahasan:
Perhatikan ilustrasi gambar berikut:
Perhatikan $\Delta APF$ dan $\Delta FHC$ merupakan dua segitiga yang sebangun, maka berlaku:
$\begin{align*} \frac{HC}{PF} &= \frac{HF}{PA} \\
\frac{y}{x} &= \frac{12}{z} \\
yz &= 12x
\end{align*}$
Perhatikan $\Delta BGE$ dan $\Delta EPA$ merupakan dua segitiga yang sebangun, maka berlaku:
$\begin{align*} \frac{BG}{EP} &= \frac{GE}{PA} \\
\frac{18-y}{12-x} &=\frac{12}{z} \\
18z - yz &=144 - 12x \\
18z - 12x &= 144 - 12x \\
18z &= 144 \\
z &= 8
\end{align*}$
$\begin{align*} Luas \ \Delta AEF &= \frac{1}{2}EF.AP \\
&= \frac{1}{2}.12.8 \\
&=48
\end{align*}$
Kunci: A
Soal LOSPI Olimpiade Guru No. 22
Perhatikan persegi panjang ABCD berukuran 9 cm x 5 cm.
Hanya DGHJ yang bukan merupakan persegi pada persegi panjang ABCD itu. Luas daerah DGHJ adalah ... cm$^2$.
A. 1,5 B. 2 C. 3 D. 3,5 E. 4
Pembahasan:
Berdasarkan informasi dan gambar maka kita peroleh:
EBCF adalah persegi dengan ukuran 5 cm x 5 cm.
AEIJ adalah persegi dengan ukuran 4 cm x 4 cm.
GFIH adalah persegi dengan ukuran 1 cm x 1 cm.
maka DGHJ adalah persegi panjang dengan ukuran 3 cm x 1 cm.
Luas DGHJ = 3 x 1 = 3 cm$^2$
Kunci: C
Soal LOSPI Olimpiade Guru No. 23
Lingkaran dengan pusat A berjari-jari 3 cm dan lingkaran dengan pusat berjari-jari 1 cm seperti terlihat pada gambar.
Jarak dari O ke D adalah ....
A. 11 cm
B. $2 \sqrt{2} + 8$ cm
C. $10 \sqrt{2}$ cm
D. $3 \sqrt{2} + 8$ cm
E. $3 \sqrt{3} + 9$ cm
Pembahasan:
Perhatikan gambar berikut ini:
IJ dan EG adalah garis singgung persekutuan luar kedua lingkaran, maka:
IJ = EG = $\sqrt{(3 + 1)^2 - (3 - 1)^2} = 2\sqrt{3}$
dengan perbandingan segitiga maka kita peroleh CJ = $\sqrt{3}$
misalkan DF = DI = x
Pada segitiga DOC berlaku pythagoras:
$OD^2 + OC^2 = CD^2$
$(x + 3)^2 + (3 + 3\sqrt{3})^2 = (x + 3\sqrt{3})^2$
$x^2 + 6x + 9 + 9 + 18\sqrt{3} + 27 = x^2 + 6x \sqrt{3} + 27$
$6x \sqrt{3} - 6x = 18\sqrt{3} + 18$
$x = \frac{18 \sqrt{3} + 18}{6 \sqrt{3} - 6}$
$x = \frac{3 \sqrt{3} + 3}{ \sqrt{3} - 1} \times \frac{\sqrt{3} + 1}{\sqrt{3} + 1}$
$x = \frac{9 + 6\sqrt{3} + 3}{3 - 1}$
$x = 6 + 3\sqrt{3}$
$OD = OF + DF$
$OD = 3 + 6 + 3\sqrt{3}$
$3\sqrt{3} + 9$
Kunci: E
Soal LOSPI Olimpiade Guru No. 24
Perhatikan gambar di bawah!
Pembahasan:
$\angle PQT$ dan $\angle SRQ$ adalah sudut dalam sepihak.
$\begin{align*} \angle PQT + \angle SRQ &= 180^o \\
41^o + \angle SRQ &= 180^o \\
\angle SRQ &= 139^o
\end{align*}$
$\begin{align*} \angle SPQ &= \angle SRQ \\
\angle SPU + \angle UPQ &= 139^o \\
83^o + \angle UPQ &= 139^o \\
\angle UPQ &= 56^o
\end{align*}$
$\begin{align*} \angle PUR + \angle URQ + \angle PQT + \angle UPQ &= 360^o \\
x + 139^o + 41^o + 56^o &= 360^o \\
x &= 124^o
\end{align*}$
Kunci: E
Soal LOSPI Olimpiade Guru No. 25
Suatu daerah dibatasi oleh persamaan: $y = 2x + 2$, $y = \frac{1}{2}x + 1$, dan $y = -\frac{3}{4}x + 7$. Berapakah nilai maksimum $y$ pada daerah tersebut?
A. $\frac{62}{11}$ B. $\frac{40}{11}$ C. $\frac{60}{11}$ D. $\frac{50}{11}$ E. $\frac{20}{11}$
Pembahasan:
Untuk mennyelesaikan persoalan ini, kita buat sketsa grafiknya terlebih dahulu untuk lebih memahaminya, perhatikan grafik berikut ini.
Dari sketsa grafik yang kita buat, maka nilai maksimum di peroleh di titik potong (titik A) antara garis $y = 2x + 2$ dan garis $y = -\frac{3}{4}x + 7$, maka kita eliminasi x.
$y = 2x + 2 \leftrightarrow 2x - y = -2$ .... pers. (1)
$y = -\frac{3}{4}x + 7 \leftrightarrow 3x + 4y = 28$ .... pers. (2)
untuk mengeliminasi x, pers. (1) dikali 3 dan pers. (2) dikali 2,
$6x - 3y = -6$
$6x + 8y = 56$
--------------------- (-)
$-11y = -62$
$y = \frac{62}{11}$
Kunci: A
Soal LOSPI Olimpiade Guru No. 26
Bilangan segitiga adalah bilangan yang berbentuk rumus $\frac{n(n + 1)}{2}$ dengan $n$ bilangan asli. Banyak bilangan segitiga yang kurang dari 100 adalah ...
A. 8 B. 9 C. 10 D. 13 E. 15
Pembahasan:
$\frac{n(n + 1)}{2} \le 100$
$n^2 + n \le 13.14 \le 200$
$n = 13$
Kunci: D
Soal LOSPI Olimpiade Guru No. 27
Diketahui jumlah 101 bilangan bulat berurutan adalah 101. Bilangan bulat terbesar di dalam barisan bilangan itu adalah ....
A. 51 B. 56 C. 100 D. 101 E. 150
Pembahasan:
Misalkan suku pertama = $a$, karena berurutan maka $b$ = 1
$\begin{align*} S_n &= \frac{n}{2} \left [2a + (n - 1)b \right ] \\
101 &= \frac{101}{2} \left (2a + 100 \right ) \\
2 &= 2a + 100 \\
-98 &= 2a \\
-49 &= a
\end{align*}$
Bilangan bulat terbesar:
$\begin{align*} U_{101} &= a + 100b \\
&= -49 + 100 \\
&= 51
\end{align*}$
Kunci: A
Soal LOSPI Olimpiade Guru No. 28
Berapakah banyak bilangan 2 digit yang nilainya 7 kali jumlah digitnya?
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
Misal: ab adalah bilangan 2 digit
ab = 7(a + b)
10a + b = 7a + 7b
3a = 6b
a = 2b
kemungkinan-kemungkinannya:
b = 1 $\rightarrow$ a = 2, maka bilangan itu adalah 21
b = 2 $\rightarrow$ a = 4, maka bilangan itu adalah 42
b = 3 $\rightarrow$ a = 6, maka bilangan itu adalah 63
b = 4 $\rightarrow$ a = 8, maka bilangan itu adalah 84
Jadi, seluruhnya ada 4.
Kunci: D
Soal LOSPI Olimpiade Guru No. 29
Pecahan $\frac{s}{t}$ adalah pecahan sejati, jika $s < t$ dan faktor persekutuan terbesar adalah 1. Jika $t$ memiliki nilai mulai dari 2 sampai dengan 9 dan $s$ bilangan bulat positif maka banyaknya pecahan sejati berbeda yang dapat dibuat adalah ....
A. 26 B. 27 C. 28 D. 30 E. 36
Pembahasan:
Jika t = 2, maka s = 1, terdapat 1 pecahan sejati.
Jika t = 3, maka s = {1, 2}, terdapat 2 pecahan sejati.
Jika t = 4, maka s = {1, 3}, terdapat 2 pecahan sejati.
Jika t = 5, maka s = {1, 2, 3, 4}, terdapat 4 pecahan sejati.
Jika t = 6, maka s = {1, 3, 5}, terdapat 3 pecahan sejati.
Jika t = 7, maka s = {1, 2, 3, 4, 5, 6}, terdapat 6 pecahan sejati.
Jika t = 8, maka s = {1, 3, 5, 7}, terdapat 4 pecahan sejati.
Jika t = 9, maka s = {1, 2, 4, 5, 7, 8}, terdapat 6 pecahan sejati.
Seluruhnya = 1 + 2 + 2 + 4 + 3 + 6 + 4 + 6 = 28 pecahan sejati.
Kunci: C
Soal LOSPI Olimpiade Guru No. 30
Bentuk sederhana dari:
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + ... + \frac{1}{2.005(2.005 + 1)}$
adalah ....
A. $\frac{2004}{2005}$
B. $\frac{2003}{2005}$
C. $\frac{2005}{2006}$
D. $\frac{2003}{2006}$
E. $\frac{2004}{2006}$
Pembahasan:
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + ... + \frac{1}{2.005(2.005 + 1)}$
=$\frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} + ... + \frac{1}{2004.2005}+ \frac{1}{2005(2006)}$
= $\left( \frac{1}{1} - \frac{1}{2} \right) + \left( \frac{1}{2} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{4} \right) + ...+ \left( \frac{1}{2004} - \frac{1}{2005} \right) + \left( \frac{1}{2005} - \frac{1}{2006} \right)$
=$1- \frac{1}{2006}$
=$\frac{2005}{2006}$
Kunci: C
Akhirnya selesai. Semoga bermanfaat bagi kita semua.
Baca juga: Soal dan Pembahasan Matematika Olimpiade Guru SMA 2018 LOSPI (No. 1 - 15)
Soal LOSPI Olimpiade Guru No. 16
Himpunan 20 buah bilangan mempunyai rata-rata 20. Sembilan di antara bilangan itu rata-ratanya 9. Rata-rata dari 11 bilangan yang tersisa adalah ...
A. 11 B. 15 C. 25 D. 29 E. 30
Pembahasan:
$n_1 = 9$ dan $\bar{x}_1$
$n_2 = 11$
$\bar{x}_{gabungan} = 20$
$\bar{x}_2 = ...?$
$\begin{align*} \bar{x}_{gabungan} &= \frac{n_1. \bar{x}_1 + n_2. \bar{x}_2}{n_1 + n_2} \\
20 &= \frac{9.9 + 11. \bar{x}_2}{9 + 11} \\
400 &= 81 + 11. \bar{x}_2 \\
319 &= 11. \bar{x}_2 \\
29 &= \bar{x}_2
\end{align*}$
Kunci: D
Soal LOSPI Olimpiade Guru No. 17
Diketahui $p$ adalah sembarang bilangan bulat positif, $2x + p = y$, $p + y = x$, dan $x + y = z$. Tentukan nilai maksimum yang mungkin dari $(x + y + z)$.
A. 10 B. -10 C. 20 D. -20 E. 30
Pembahasan:
Diketahui:
$p > 0$
$2x + p = y$ ...... pers. (1)
$p + y = x$ ........ pers. (2)
$x + y = z$ ........ pers. (3)
Jumlahkan pers. (1) dengan (2), diperoleh:
$2x + 2p + y = x + y$
$x + 2p = 0$
$x = -2p$
$2x + p = y$
$2.(-2p) + p = y$
$-3p = y$
Substitusi ke pers. (3)
x + y = z
-2p - 3p = z
-5p = z
Nilai maksimum (bernilai positif)
= x + y + z
= 2p + 3p + 5p
= 10p
Kunci: A
Soal LOSPI Olimpiade Guru No. 18
Perhatikan gambar berikut ini:
Bila panjang BP = $\sqrt{160}$, tentukan panjang CP.
A. 10 B. 12 C. 13 D. 14 E. 15
Pembahasan:
Dengan Teorema Bendera Inggris (British Flag Teorem):
$\begin{align*} AP^2 + CP^2 &= BP^2 + DP^2 \\
5^2 + CP^2 &= (\sqrt{160})^2 + 3^2 \\
25 + CP^2 &= 160 + 9 \\
CP^2 &= 144 \\
CP^2 &= 12
\end{align*}$
Kunci: B
Soal LOSPI Olimpiade Guru No. 19
Hitunglah: $\frac{(2008-2007)^2 + (2008 + 2007)^2}{2008^2 + 2007^2}$
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
$\frac{(2008-2007)^2 + (2008 + 2007)^2}{2008^2 + 2007^2}$
$= \frac{2008^2 - 2.2008.2007 + 2007^2 + 2008^2 + 2.200.2007 + 2007^2}{2008^2 + 2007^2}$
$= \frac{2(2008^2 + 2007^2)}{2008^2 + 2007^2}$
=2
Kunci: B
Soal LOSPI Olimpiade Guru No. 20
Hitunglah: $\frac{657 \times 657 \times 657 - 368 \times 368 \times 368}{657 \times 657 + 657 \ times 368 + 368 \times 368}$
A. 273 B. 285 C. 289 D. 290 E. 292
Pembahasan:
Ingat: $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$
$\begin{align*} &\frac{657 \times 657 \times 657 - 368 \times 368 \times 368}{657 \times 657 + 657 \times 368 + 368 \times 368} \\
&= \frac{657^3 - 368^3}{657^2 + 657 \times 368 + 368^2} \\
&= \frac{(657 - 368)(657^2 + 657 \times 368 + 368^2)}{657^2 + 657 \times 368 + 368^2} \\
&= 657 - 368 \\
&= 289
\end{align*}$
Kunci: C
Soal LOSPI Olimpiade Guru No. 21
Perhatikan gambar!
Segitiga ABC adalah segitiga sama kaki dengan AB = BC dan BC = 30 cm. Persegi EFGH mempunyai panjang sisi 12 cm, maka luas segitiga AEF adalah ... cm$^2$.
A. 48 B. 49 C. 50 D. 51 E. 53
Pembahasan:
Perhatikan ilustrasi gambar berikut:
Perhatikan $\Delta APF$ dan $\Delta FHC$ merupakan dua segitiga yang sebangun, maka berlaku:
$\begin{align*} \frac{HC}{PF} &= \frac{HF}{PA} \\
\frac{y}{x} &= \frac{12}{z} \\
yz &= 12x
\end{align*}$
Perhatikan $\Delta BGE$ dan $\Delta EPA$ merupakan dua segitiga yang sebangun, maka berlaku:
$\begin{align*} \frac{BG}{EP} &= \frac{GE}{PA} \\
\frac{18-y}{12-x} &=\frac{12}{z} \\
18z - yz &=144 - 12x \\
18z - 12x &= 144 - 12x \\
18z &= 144 \\
z &= 8
\end{align*}$
$\begin{align*} Luas \ \Delta AEF &= \frac{1}{2}EF.AP \\
&= \frac{1}{2}.12.8 \\
&=48
\end{align*}$
Kunci: A
Soal LOSPI Olimpiade Guru No. 22
Perhatikan persegi panjang ABCD berukuran 9 cm x 5 cm.
Hanya DGHJ yang bukan merupakan persegi pada persegi panjang ABCD itu. Luas daerah DGHJ adalah ... cm$^2$.
A. 1,5 B. 2 C. 3 D. 3,5 E. 4
Pembahasan:
Berdasarkan informasi dan gambar maka kita peroleh:
EBCF adalah persegi dengan ukuran 5 cm x 5 cm.
AEIJ adalah persegi dengan ukuran 4 cm x 4 cm.
GFIH adalah persegi dengan ukuran 1 cm x 1 cm.
maka DGHJ adalah persegi panjang dengan ukuran 3 cm x 1 cm.
Luas DGHJ = 3 x 1 = 3 cm$^2$
Kunci: C
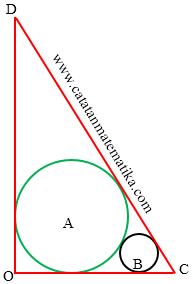
Soal LOSPI Olimpiade Guru No. 23
Lingkaran dengan pusat A berjari-jari 3 cm dan lingkaran dengan pusat berjari-jari 1 cm seperti terlihat pada gambar.
Jarak dari O ke D adalah ....
A. 11 cm
B. $2 \sqrt{2} + 8$ cm
C. $10 \sqrt{2}$ cm
D. $3 \sqrt{2} + 8$ cm
E. $3 \sqrt{3} + 9$ cm
Pembahasan:
Perhatikan gambar berikut ini:
IJ dan EG adalah garis singgung persekutuan luar kedua lingkaran, maka:
IJ = EG = $\sqrt{(3 + 1)^2 - (3 - 1)^2} = 2\sqrt{3}$
dengan perbandingan segitiga maka kita peroleh CJ = $\sqrt{3}$
misalkan DF = DI = x
Pada segitiga DOC berlaku pythagoras:
$OD^2 + OC^2 = CD^2$
$(x + 3)^2 + (3 + 3\sqrt{3})^2 = (x + 3\sqrt{3})^2$
$x^2 + 6x + 9 + 9 + 18\sqrt{3} + 27 = x^2 + 6x \sqrt{3} + 27$
$6x \sqrt{3} - 6x = 18\sqrt{3} + 18$
$x = \frac{18 \sqrt{3} + 18}{6 \sqrt{3} - 6}$
$x = \frac{3 \sqrt{3} + 3}{ \sqrt{3} - 1} \times \frac{\sqrt{3} + 1}{\sqrt{3} + 1}$
$x = \frac{9 + 6\sqrt{3} + 3}{3 - 1}$
$x = 6 + 3\sqrt{3}$
$OD = OF + DF$
$OD = 3 + 6 + 3\sqrt{3}$
$3\sqrt{3} + 9$
Kunci: E
Soal LOSPI Olimpiade Guru No. 24
Perhatikan gambar di bawah!
Diketahui $\angle PST = 83^o$ dan $\angle PQT = 41$^o$. Garis PQ dan RS sejajar, demikian juga garis PS dan QT sejajar. Berapakah besar sudut x?
A. 120$^o$ B. 121$^o$ C. 122$^o$ D. 123$^o$ E. 124$^o$Pembahasan:
$\angle PQT$ dan $\angle SRQ$ adalah sudut dalam sepihak.
$\begin{align*} \angle PQT + \angle SRQ &= 180^o \\
41^o + \angle SRQ &= 180^o \\
\angle SRQ &= 139^o
\end{align*}$
$\begin{align*} \angle SPQ &= \angle SRQ \\
\angle SPU + \angle UPQ &= 139^o \\
83^o + \angle UPQ &= 139^o \\
\angle UPQ &= 56^o
\end{align*}$
$\begin{align*} \angle PUR + \angle URQ + \angle PQT + \angle UPQ &= 360^o \\
x + 139^o + 41^o + 56^o &= 360^o \\
x &= 124^o
\end{align*}$
Kunci: E
Soal LOSPI Olimpiade Guru No. 25
Suatu daerah dibatasi oleh persamaan: $y = 2x + 2$, $y = \frac{1}{2}x + 1$, dan $y = -\frac{3}{4}x + 7$. Berapakah nilai maksimum $y$ pada daerah tersebut?
A. $\frac{62}{11}$ B. $\frac{40}{11}$ C. $\frac{60}{11}$ D. $\frac{50}{11}$ E. $\frac{20}{11}$
Pembahasan:
Untuk mennyelesaikan persoalan ini, kita buat sketsa grafiknya terlebih dahulu untuk lebih memahaminya, perhatikan grafik berikut ini.
Dari sketsa grafik yang kita buat, maka nilai maksimum di peroleh di titik potong (titik A) antara garis $y = 2x + 2$ dan garis $y = -\frac{3}{4}x + 7$, maka kita eliminasi x.
$y = 2x + 2 \leftrightarrow 2x - y = -2$ .... pers. (1)
$y = -\frac{3}{4}x + 7 \leftrightarrow 3x + 4y = 28$ .... pers. (2)
untuk mengeliminasi x, pers. (1) dikali 3 dan pers. (2) dikali 2,
$6x - 3y = -6$
$6x + 8y = 56$
--------------------- (-)
$-11y = -62$
$y = \frac{62}{11}$
Kunci: A
Soal LOSPI Olimpiade Guru No. 26
Bilangan segitiga adalah bilangan yang berbentuk rumus $\frac{n(n + 1)}{2}$ dengan $n$ bilangan asli. Banyak bilangan segitiga yang kurang dari 100 adalah ...
A. 8 B. 9 C. 10 D. 13 E. 15
Pembahasan:
$\frac{n(n + 1)}{2} \le 100$
$n^2 + n \le 13.14 \le 200$
$n = 13$
Kunci: D
Soal LOSPI Olimpiade Guru No. 27
Diketahui jumlah 101 bilangan bulat berurutan adalah 101. Bilangan bulat terbesar di dalam barisan bilangan itu adalah ....
A. 51 B. 56 C. 100 D. 101 E. 150
Pembahasan:
Misalkan suku pertama = $a$, karena berurutan maka $b$ = 1
$\begin{align*} S_n &= \frac{n}{2} \left [2a + (n - 1)b \right ] \\
101 &= \frac{101}{2} \left (2a + 100 \right ) \\
2 &= 2a + 100 \\
-98 &= 2a \\
-49 &= a
\end{align*}$
Bilangan bulat terbesar:
$\begin{align*} U_{101} &= a + 100b \\
&= -49 + 100 \\
&= 51
\end{align*}$
Kunci: A
Soal LOSPI Olimpiade Guru No. 28
Berapakah banyak bilangan 2 digit yang nilainya 7 kali jumlah digitnya?
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
Misal: ab adalah bilangan 2 digit
ab = 7(a + b)
10a + b = 7a + 7b
3a = 6b
a = 2b
kemungkinan-kemungkinannya:
b = 1 $\rightarrow$ a = 2, maka bilangan itu adalah 21
b = 2 $\rightarrow$ a = 4, maka bilangan itu adalah 42
b = 3 $\rightarrow$ a = 6, maka bilangan itu adalah 63
b = 4 $\rightarrow$ a = 8, maka bilangan itu adalah 84
Jadi, seluruhnya ada 4.
Kunci: D
Soal LOSPI Olimpiade Guru No. 29
Pecahan $\frac{s}{t}$ adalah pecahan sejati, jika $s < t$ dan faktor persekutuan terbesar adalah 1. Jika $t$ memiliki nilai mulai dari 2 sampai dengan 9 dan $s$ bilangan bulat positif maka banyaknya pecahan sejati berbeda yang dapat dibuat adalah ....
A. 26 B. 27 C. 28 D. 30 E. 36
Pembahasan:
Jika t = 2, maka s = 1, terdapat 1 pecahan sejati.
Jika t = 3, maka s = {1, 2}, terdapat 2 pecahan sejati.
Jika t = 4, maka s = {1, 3}, terdapat 2 pecahan sejati.
Jika t = 5, maka s = {1, 2, 3, 4}, terdapat 4 pecahan sejati.
Jika t = 6, maka s = {1, 3, 5}, terdapat 3 pecahan sejati.
Jika t = 7, maka s = {1, 2, 3, 4, 5, 6}, terdapat 6 pecahan sejati.
Jika t = 8, maka s = {1, 3, 5, 7}, terdapat 4 pecahan sejati.
Jika t = 9, maka s = {1, 2, 4, 5, 7, 8}, terdapat 6 pecahan sejati.
Seluruhnya = 1 + 2 + 2 + 4 + 3 + 6 + 4 + 6 = 28 pecahan sejati.
Kunci: C
Soal LOSPI Olimpiade Guru No. 30
Bentuk sederhana dari:
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + ... + \frac{1}{2.005(2.005 + 1)}$
adalah ....
A. $\frac{2004}{2005}$
B. $\frac{2003}{2005}$
C. $\frac{2005}{2006}$
D. $\frac{2003}{2006}$
E. $\frac{2004}{2006}$
Pembahasan:
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + ... + \frac{1}{2.005(2.005 + 1)}$
=$\frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} + ... + \frac{1}{2004.2005}+ \frac{1}{2005(2006)}$
= $\left( \frac{1}{1} - \frac{1}{2} \right) + \left( \frac{1}{2} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{4} \right) + ...+ \left( \frac{1}{2004} - \frac{1}{2005} \right) + \left( \frac{1}{2005} - \frac{1}{2006} \right)$
=$1- \frac{1}{2006}$
=$\frac{2005}{2006}$
Kunci: C
Akhirnya selesai. Semoga bermanfaat bagi kita semua.
Baca juga: Soal dan Pembahasan Matematika Olimpiade Guru SMA 2018 LOSPI (No. 1 - 15)









Mantap pak.. ini sangat membantu saya dalam bermatematik.. ditunggu tulisan berikutnya
ReplyDeleteOke pak. Terima kasih....!
DeleteBagaimana cara download pembahasan olimpiade Matematika Guru SMA nya?
ReplyDeleteMaaf mas! Saya tidak menyediakan pembahasannya dalam bentuk file. Saran: sebaiknya print langsung.😊😊😊
DeleteMaaf kak,, soal no 28 dari mana datang 10a nya ya,, Terimakasih banyak min🙏🙏
ReplyDeleteab itu bilangan puluhan (bilangan dua angka), dimana a puluhan maka 10.a dan b satuan maka b. Contoh 53 = 10 x 5 + 3
Delete