Transformasi Geometri 2. Refleksi (Pencerminan)

A. Definisi Transformasi Refleksi (Pencerminan)

Refleksi atau pencerminan merupakan transformasi isometri berhadapan yang memindahkan semua titik pada bangun yang ditransformasi ke arah garis/cermin sejauh dua kali jarak bangun terhadap garis/cermin.

B. Beberapa Bentuk Refleksi (Pencerminan)

1.	Pencerminan terhadap sumbu X $P(x,y)\xrightarrow{\text{M }[\text{ sumbu}\,X]}P'(x,-y)$
2.	Pencerminan terhadap sumbu Y $P(x,y)\xrightarrow{\text{M }[\text{ sumbu}\,Y]}P'(-x,y)$
3.	Pencerminan terhadap garis $y=x$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=x]}P'(y,x)$
4.	Pencerminan terhadap garis $y=-x$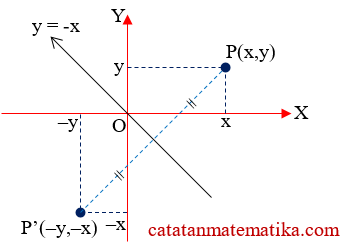 $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=-x]}P'(-y,-x)$
5.	Pencerminan terhadap titik pusat $O(0,0)$ $P(x,y)\xrightarrow{\text{M }[\text{ titik }O(0,0)]}P'(-x,-y)$
6.	Pencerminan terhadap garis $x=h$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,x=h]}P'(2h-x,y)$
7.	Pencerminan terhadap garis $y=k$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=k]}P'(x,2k-y)$
8.	Pencerminan berurutan terhadap garis $x=h$ dilanjutkan tehadap garis $y=k$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,x=h\,\text{dan}\,y=k]}P'(2h-x,2k-y)$
9.	Pencerminan titik $P(x,y)$ terhadap garis $x=h$ dilanjutkan terhadap garis $x=k$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,x=h\,\text{dan}\,x=k]}P'(2(k-h)+x,y)$
10.	Pencerminan titik $P(x,y)$ terhadap garis $y=h$ dilanjutkan terhadap garis $y=k$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=h\,\text{dan}\,y=k]}P'(x,2(k-h)+y)$
11.	Pencerminan terhadap garis $y=mx$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=mx]}P'(x',y')$ maka $\left( \begin{matrix}x' \\ y' \\ \end{matrix} \right)=\left( \begin{matrix} \frac{1-m^2}{1+m^2} & \frac{2m}{1+m^2} \\ \frac{2m}{1+m^2} & -\frac{1-m^2}{1+m^2} \\ \end{matrix} \right)\left( \begin{matrix} x \\ y \\ \end{matrix} \right)$.
12.	Pencerminan terhadap garis $y=mx+n$ $P(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=mx+n]}P'(x',y')$ maka $\left( \begin{matrix} x' \\ y'-n \\ \end{matrix} \right)=\left( \begin{matrix} \frac{1-m^2}{1+m^2} & \frac{2m}{1+m^2} \\ \frac{2m}{1+m^2} & -\frac{1-m^2}{1+m^2} \\ \end{matrix} \right)\left( \begin{matrix} x \\ y-n \\ \end{matrix} \right)$.

---

Contoh 1.
Tentukan bayangan dari titik-titik berikut ini!
a. $A(2,5)$ oleh refleksi terhadap sumbu X.
b. $B(7,-4)$ oleh refleksi terhadap sumbu Y.
c. $C(-4,3)$ oleh refleksi terhadap garis $y=x$.
d. $D(-3,-1)$ oleh refleksi terhadap garis $y=-x$.
e. $E(3,6)$ oleh refleksi terhadap garis $x=-2$.
f. $G(5,7)$ oleh refleksi terhadap garis $y=3$.
g. $H(4,2)$ oleh refleksi terhadap titik pangkal O.
Penyelesaian:
a. $(x,y)\xrightarrow{\text{M }[\text{ sumbu}\,X]}(x,-y)$ maka $A(2,5)\xrightarrow{\text{M }[\text{ sumbu}\,X]}A'(2,-5)$
b. $(x,y)\xrightarrow{\text{M }[\text{ sumbu}\,Y]}(-x,y)$ maka $B(7,-4)\xrightarrow{\text{M }[\text{ sumbu}\,Y]}B'(-7,-4)$
c. $(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=x]}(y,x)$ maka $C(-4,3)\xrightarrow{\text{M }[\text{ garis}\,y=x]}C'(3,-4)$
d. $(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=-x]}(-y,-x)$ maka $D(-3,1)\xrightarrow{\text{M }[\text{ garis}\,y=-x]}D'(-1,3)$
e. $(x,y)\xrightarrow{\text{M }[\text{ garis}\,x=h]}(2h-x,y)$ maka $E(3,6)\xrightarrow{\text{M }[\text{ garis}\,x=-2]}D'(2(-2)-3,6)=D'(-7,6)$
f. $(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=k]}(x,2k-y)$ maka $G(5,7)\xrightarrow{\text{M }[\text{ garis}\,y=3]}G'(5,2.3-7)=G'(5,-1)$
g. $(x,y)\xrightarrow{\text{M }[\text{ titik }O(0,0)]}(-x,-y)$ maka $H(4,2)\xrightarrow{\text{M }[\text{ titik }O(0,0)]}H'(-4,-2)$

---

Contoh 2.
Tentukan bayangan dari garis $x+2y-5=0$ yang ditransformasikan oleh refleksi terhadap garis $x=3$.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ garis}\,x=3]}(2.3-x,y)=(\underbrace{6-x}_{x'},\underbrace{y}_{y'})$
$\begin{align}6-x &= x' \\ -x &= x'-6 \\ x &= -x'+6 \end{align}$
$y=y'$
Substitusi $x=-x'+6$ dan $y=y'$ ke persamaan:
$\begin{align}x+2y-5 &= 0 \\ -x'+6+2y'-5 &= 0 \\ -x'+2y'+5 &= 0 \\ x'-2y'-5 &= 0 \end{align}$
Jadi, bayangan dari garis $x+2y-5=0$ yang ditransformasikan oleh refleksi terhadap garis $x=3$ adalah $x-2y-5=0$.

---

Contoh 3.
Tentukan bayangan garis $2y-3x+6=0$ jika dicerminkan terhadap sumbu X.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ sumbu}\,X]}(\underbrace{x}_{x'},\underbrace{-y}_{y'})$
$x=x'$
$\begin{align}-y &= y' \\ y &= -y' \end{align}$
Substitusi $x=x'$ dan $y=-y'$ ke persamaan:
$\begin{align}2y-3x+6 &= 0 \\ 2(-y')-3x'+6 &= 0 \\ -2y'-3x'+6 &= 0 \\ 3x'+2y'-6 &= 0 \end{align}$
Jadi, bayangan garis $2y-3x+6=0$ jika dicerminkan terhadap sumbu X adalah $3x+2y-6=0$.

---

Contoh 4.
Tentukan bayangan parabola $y=x^2-3x+2$ jika dicerminkan terhadap sumbu Y.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ sumbu}\,Y]}(\underbrace{-x}_{x'},\underbrace{y}_{y'})$
$\begin{align}-x &= x' \\ x &= -x' \end{align}$
$y=y'$
Substitusi $x=-x'$ dan $y=y'$ ke persamaan:
$\begin{align}y &= x^2-3x+2 \\ y' &= (-x')^2-3x'+2 \\ y' &= (x')^2-3x'+2 \end{align}$
Jadi, bayangan parabola $y=x^2-3x+2$ jika dicerminkan terhadap sumbu Y adalah $y=x^2-3x+2$.

---

Contoh 5.
Tentukan bayangan parabola $x={{y}^{2}}-2y-2$ jika dicerminkan terhadap garis $y=x$.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=x]}(\underbrace{y}_{x'},\underbrace{x}_{y'})$
$y=x'$ dan $x=y'$
Substitusi ke persamaan:
$\begin{align}x &= y^2-2y-2 \\ y' &= (x')^2-2x'-2 \end{align}$
Jadi, bayangan parabola $x=y^2-2y-2$ jika dicerminkan terhadap garis $y=x$ adalah $y=x^2-2x-2$.

---

Contoh 6.
Tentukan bayangan lingkaran $x^2+{{y}^{2}}-2x+2y-3=0$ jika dicerminkan terhadap garis $y=-x$.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=-x]}(\underbrace{-y}_{x'},\underbrace{-x}_{y'})$
$-y=x'\to y=-x'$
$-x=y'\to x=-y'$
Substitusi $y=-x'$ dan $x=-y'$ ke persamaan:
$\begin{align}x^2+y^2-2x+2y-3 &= 0 \\ (-y')^2+(-x')^2-2(-y')+2(-x')-3 &= 0 \\ (y')^2+(x')^2+2y'-2x'-3 &= 0 \\ (x')^2+(y')^2-2x'+2y'-3 &= 0 \end{align}$
Jadi, bayangan lingkaran $x^2+y^2-2x+2y-3=0$ jika dicerminkan terhadap garis $y=-x$ adalah $x^2+y^2-2x+2y-3=0$.

---

Contoh 7.
Titik $P(15,-18)$ dicerminkan terhadap garis $x=7$ kemudian dicerminkan terhadap garis $y=-3$. Tentukan koordinat bayangan akhir dari titik P.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ garis}\,x=h\,\text{dan}\,y=k]}(2h-x,2k-y)$ maka:
$P(15,-18)\xrightarrow{\text{M }[\text{ garis}\,x=7\,\text{dan}\,y=-3]}P'(x',y')$
$\begin{align}P'(x',y') &= P'(2h-x,2k-y) \\ &= P'(2.7-15,2(-3)+18) \\ &= P'(-1,12) \end{align}$

---

Contoh 8.
Tentukan bayangan dari $(2,-4)$ oleh refleksi berurutan terhadap $x=3$, kemudian $x=7$.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ garis}\,x=h\,\text{dan}\,x=k]}(2(k-h)+x,y)$ maka:
$(2,-4)\xrightarrow{\text{M }[\text{ garis}\,x=3\,\text{dan}\,x=7]}(x',y')$
$\begin{align}(x',y') &= (2(k-h)+x,y) \\ &= (2(7-3)+2,-4) \\ &= (10,-4) \end{align}$

---

Contoh 9.
Tentukan bayangan dari titik $(3,1)$ jika direfleksikan terhadap garis $y=3x$.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=mx]}(x',y')$ maka $\left( \begin{matrix} x' \\ y' \\ \end{matrix} \right)=\left( \begin{matrix} \frac{1-m^2}{1+m^2} & \frac{2m}{1+m^2} \\ \frac{2m}{1+m^2} & -\frac{1-m^2}{1+m^2} \\ \end{matrix} \right)\left( \begin{matrix} x \\ y \\ \end{matrix} \right)$.
$(3,1)\xrightarrow{\text{M }[\text{ garis}\,y=3x]}(x',y')$ maka:
$\begin{align}\left( \begin{matrix} x' \\ y' \\ \end{matrix} \right) &= \left( \begin{matrix} \frac{1-m^2}{1+m^2} & \frac{2m}{1+m^2} \\ \frac{2m}{1+m^2} & -\frac{1-m^2}{1+m^2} \\ \end{matrix} \right)\left( \begin{matrix} x \\ y \\ \end{matrix} \right) \\ &= \left( \begin{matrix}\frac{1-3^2}{1+3^2} & \frac{2.3}{1+3^2} \\ \frac{2.3}{1+3^2} & -\frac{1-3^2}{1+3^2} \\ \end{matrix} \right)\left( \begin{matrix} 3 \\ 1 \\ \end{matrix} \right) \\ &= \left( \begin{matrix} -\frac{8}{10} & \frac{6}{10} \\ \frac{6}{10} & \frac{8}{10} \\ \end{matrix} \right)\left( \begin{matrix} 3 \\ 1 \\ \end{matrix} \right) \\ &= \left( \begin{matrix} -\frac{4}{5} & \frac{3}{5} \\ \frac{3}{5} & \frac{4}{5} \\ \end{matrix} \right)\left( \begin{matrix} 3 \\ 1 \\ \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y' \\ \end{matrix} \right) &= \left( \begin{matrix} -\frac{9}{5} \\ \frac{7}{5} \\ \end{matrix} \right) \end{align}$
Jadi, bayangan dari titik $(3,1)$ jika direfleksikan terhadap garis $y=3x$ adalah $\left( -\frac{9}{5},\frac{7}{5} \right)$.

---

Contoh 10.
Tentukan bayangan dari titik $(-2,5)$ jika direfleksikan ke garis $y=-2x+3$.
Penyelesaian:
$(x,y)\xrightarrow{\text{M }[\text{ garis}\,y=mx+n]}(x',y')$ maka $\left( \begin{matrix} x' \\ y'-n \\ \end{matrix} \right) = \left( \begin{matrix} \frac{1-m^2}{1+m^2} & \frac{2m}{1+m^2} \\ \frac{2m}{1+m^2} & -\frac{1-m^2}{1+m^2} \\ \end{matrix} \right)\left( \begin{matrix} x \\ y-n \\ \end{matrix} \right)$.
$(-2,5)\xrightarrow{\text{M }[\text{ garis}\,y=-2x+3]}(x',y')$ maka:
$\begin{align}\left( \begin{matrix} x' \\ y'-n \\ \end{matrix} \right) &= \left( \begin{matrix} \frac{1-m^2}{1+m^2} & \frac{2m}{1+m^2} \\ \frac{2m}{1+m^2} & -\frac{1-m^2}{1+m^2} \\ \end{matrix} \right)\left( \begin{matrix} x \\ y-n \\ \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y'-3 \\ \end{matrix} \right) &= \left( \begin{matrix} \frac{1-(-2)^2}{1+(-2)^2} & \frac{2(-2)}{1+(-2)^2} \\\frac{2(-2)}{1+(-2)^2} & -\frac{1-(-2)^2}{1+(-2)^2} \\\end{matrix} \right)\left( \begin{matrix} -2 \\ 5-3 \\ \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y'-3 \\ \end{matrix} \right) &= \left( \begin{matrix} \frac{-3}{5} & \frac{-4}{5} \\ \frac{-4}{5} & \frac{3}{5} \\ \end{matrix} \right)\left( \begin{matrix} -2 \\ 2 \\ \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y'-3 \\ \end{matrix} \right) &= \left( \begin{matrix} \frac{6}{5}-\frac{8}{5} \\ \frac{8}{5}+\frac{6}{5} \\ \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y'-3 \\ \end{matrix} \right) &= \left( \begin{matrix} -\frac{2}{5} \\ \frac{14}{5} \\ \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y' \\ \end{matrix} \right) &= \left( \begin{matrix} -\frac{2}{5} \\ \frac{14}{5}+3 \\ \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y' \\ \end{matrix} \right) &= \left( \begin{matrix} -\frac{2}{5} \\ \frac{29}{5} \\ \end{matrix} \right) \end{align}$.
Jadi, bayangan dari titik $(-2,5)$ jika direfleksikan ke garis $y=-2x+3$ adalah $\left( -\frac{2}{5},\frac{29}{5} \right)$.

---

C. Soal Latihan

1.	Koordinat titik sudut segitiga ABC adalah $A(2,1)$, $B(1,4)$ dan $C(-2,2)$. Tentukan koordinat titik sudut hasil bayangan setelah direfleksi terhadap sumbu X.
2.	Tentukan bayangan titik $(-4,2)$ jika direfleksikan terhadap garis $y=-x$.
3.	Tentukan bayangan titik $P(-4,5)$ oleh refleksi terhadap garis $y=-x$ dilanjutkan dengan refleksi terhadap garis $x=2$.
4.	Tentukan bayangan dari titik $A(-3,2)$ yang direfleksikan terhadap garis $x=-2$ dilanjutkan terhadap garis $y=3$.
5.	Tentukan bayangan garis $x-2y=3$ jika refleksikan terhadap sumbu Y.

Semoga postingan: Transformasi Geometri 2. Refleksi (Pencerminan) ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :