Lingkaran 2. Persamaan Lingkaran dengan Pusat P(a,b) dan Jari-jari r

A. Persamaan Lingkaran dengan Pusat $P(a,b)$ dan Jari-jari $r$

Perhatikan gambar berikut ini!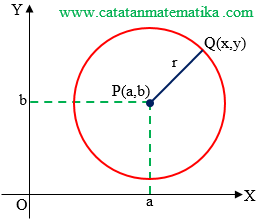

Titik $Q(x,y)$ terletak pada lingkaran yang berpusat di titik $P(a,b)$ dan jari-jari $r$.
Berdasarkan definisi lingkaran maka tempat kedudukan titik $Q(x,y)$ adalah:
$\{Q(x,y)|PQ=r\}$
$\{Q(x,y)|\sqrt{(x-a)^2+(y-b)^2}=r\}$
$\{Q(x,y)|(x-a)^2+(y-b)^2=r^2\}$

Jadi, persamaan lingkaran dengan pusat $P(a,b)$ dan jari-jari $r$ adalah:
$(x-a)^2+(y-b)^2=r^2$

Contoh 1.
Tentukan persamaan lingkaran dengan pusat $P(3,-4)$ dan jari-jari 7.
Penyelesaian:
Titik pusat lingkaran $P(3,-4)=P(a,b)$ dan jari-jari $r=7$
Persamaan lingkaran:
$\begin{align}(x-a)^2+(y-b)^2 &= r^2 \\ (x-3)^2+(y+4)^2 &= 7^2 \\ x^2-6x+9+y^2+8y+16 &= 49 \\ x^2+y^2-6x+8y+25-49 &= 0 \\ x^2+y^2-6x+8y-24 &= 0 \end{align}$

Contoh 2.
Tentukan persamaan lingkaran dengan titik pusat $P(1,2)$ dan melalui titik $(5,-3)$.
Penyelesaian:
Persamaan lingkaran dengan pusat $P(1,2)=P(a,b)$adalah:
$(x-a)^2+(y-b)^2=r^2$
melalui titik $(5,-3)=(x,y)$, substitusi ke persamaan maka:
$\begin{align}(x-1)^2+(y-2)^2 &= r^2 \\ (5-1)^2+(-3-2)^2 &= r^2 \\ 16+25 &= r^2 \\ r^2 &= 41 \end{align}$
Persamaan lingkaran:
$\begin{align}(x-1)^2+(y-2)^2 &= r^2 \\ (x-1)^2+(y-2)^2 &= 41 \\ x^2-2x+1+y^2-4y+4 &= 41 \\ x^2+y^2-2x-4y+5-41 &= 0 \\ x^2+y^2-2x-4y-36 &= 0 \end{align}$

Contoh 3.
Tentukan pusat dan jari-jari dari persamaan lingkaran $(x+5)^2+(y-6)^2=16$.
Penyelesaian:
$\begin{align}(x+5)^2+(y-6)^2 &= 16 \\ (x-a)^2+(y-b)^2 &= r^2 \end{align}$
$-a=5\Leftrightarrow a=-5$
$-b=-6\Leftrightarrow b=6$
$r^2=16\Leftrightarrow r=4$
Jadi, titik pusat lingkaran adalah $P(a,b)=P(-5,6)$ dan jari-jari $r=4$.

Contoh 4.
Tentukan persamaan lingkaran yang berdiameter ruas garis AB dengan $A(2,1)$ dan $B(-2,3)$.
Penyelesaian:
AB adalah diameter lingkaran maka:
$\begin{align}d &= AB \\ &= \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} \\ &= \sqrt{(-2-2)^2+(3-1)^2} \\ &= \sqrt{16+4} \\ &= \sqrt{20} \\ d &= 2\sqrt{5} \end{align}$
Jari-jari lingkaran adalah:
$\begin{align}r &= \frac{1}{2}d \\ &= \frac{1}{2}.2\sqrt{5} \\ r &= \sqrt{5} \end{align}$

Titik pusat lingkaran adalah titik tengah ruas garis AB yaitu:
$\left( \frac{x_A+x_B}{2},\frac{y_A+y_B}{2} \right)=\left( \frac{2+(-2)}{2},\frac{1+3}{2} \right)=(0,2)$
Jadi, persamaan lingkaran dengan pusat $P(0,2)=P(a,b)$ dan jari-jari $r=\sqrt{5}$ adalah:
$\begin{align}(x-a)^2+(y-b)^2 &= r^2 \\ (x-0)^2+(y-2)^2 &= \left( \sqrt{5} \right)^2 \\ x^2+y^2-4y+4 &= 5 \\ x^2+y^2-4y+4-5 &= 0 \\ x^2+y^2-4y-1 &= 0 \end{align}$

Contoh 5.
Tentukan persamaan lingkaran yang pusat $P(3,4)$ dan menyinggung garis $3x+y=3$.
Penyelesaian:
Persamaan garis:
$3x+y=3\Leftrightarrow 3x+y-3=0$
Perhatikan sketsa gambar berikut!

Dari gambar diperoleh bahwa jari-jari lingkaran adalah jarak titik $P(3,4)=({{x}_{1}},{{y}_{1}})$ ke garis $3x+y-3=0\Leftrightarrow ax+by+c=0$ maka:
$\begin{align}r &= \left| \frac{ax_1+by_1+c}{\sqrt{a^2+b^2}} \right| \\ &= \left| \frac{3.3+1.4-3}{\sqrt{3^2+1^2}} \right| \\ &= \left| \frac{9+4-3}{\sqrt{9+1}} \right| \\ &= \left| \frac{10}{\sqrt{10}} \right| \\ &= \left| \sqrt{10} \right| \\ r &= \sqrt{10} \end{align}$
Jadi, persamaan lingkaran dengan pusat $P(3,4)=(a,b)$ dan jari-jari $r=\sqrt{10}$ adalah:
$\begin{align}(x-a)^2+(y-b)^2 &= r^2 \\ (x-3)^2+(y-4)^2 &= \left( \sqrt{10} \right)^2 \\ x^2-6x+9+y^2-8y+16 &= 10 \\ x^2+y^2-6x-8y+25-10 &= 0 \\ x^2+y^2-6x-8y+15 &= 0 \end{align}$

B. Soal Latihan

1. Tentukan persamaan lingkaran yang berpusat di titik $(4,0)$ dan berdiameter $6\sqrt{2}$.
2. Tentukan persamaan lingkaran yang berpusat di titik $P(-4,1)$ dan melalui titik $(3,4)$.
3. Tentukan persamaan lingkaran yang salah satu ujung diameternya $(5,-2)$ dan $(-1,8)$.
4. Tentukan persamaan lingkaran dengan pusat $P(3,1)$ dan menyinggung garis $3x+4y+7=0$.
5. Tentukan persamaan lingkaran yang berpusat di titik $(1,-10)$ dan menyinggung garis $3x-y\sqrt{3}-3=0$.

Semoga postingan: Lingkaran 2. Persamaan Lingkaran dengan Pusat P(a,b) dan Jari-jari r ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :