Pembahasan Matematika IPA SBMPTN 2018 Kode 407
Matematika IPA SBMPTN 2018 Kode 407 No. 1
Jika nilai maksimum dan minimum fungsi $f(x)=a\cos x+b$ berturut-turut adalah 6 dan 2, maka nilai minimum fungsi $g(x)=2a\sin x+3b$ adalah …
A. -4 B. -2 C. 2 D. 4 E. 8
Pembahasan:
$f(x)=a\cos x+b$, Nilai maksimum = a + b, nilai minimum –a + b
$a+b=6$
$-a+b=2$
------------- (+)
$2b=8\Rightarrow b=4,a=2$
$g(x)=2a\sin x+3b$
$g(x)=4\sin x+12$
Nilai minimum = -4 + 12 = 8
Kunci: E
Diketahui gradien garis yang melalui titik O(0,0) dan P(a,b) adalah -3. Jika P dicerminkan terhadap sumbu y kemudian digeser 5 satuan ke atas dan 2 satuan ke kanan, maka gradien garis yang melalui P’ dan O(0,0) adalah 2. Titik P adalah …
A. (-2,6) B. (-1,3) C. (1,-3) D. (2,-6) E. (3,-9)
Pembahasan:
Gradien garis melalui O(0,0) dan P(a,b) adalah -3, maka:
$\frac{b}{a}=-3\Leftrightarrow b=-3a$
$P(a,b)\overset{C(sumbu-y)}{\mathop{\Rightarrow }}\,(-a,b)\overset{\left( \begin{smallmatrix}
2 \\
5
\end{smallmatrix} \right)}{\mathop{\Rightarrow }}\,P'(-a+2,b+5)$
Gradien garis melalui O(0,0) dan P’(-a + 2, b + 5) adalah 2, maka:
$\frac{b+5}{-a+2}=2$
$-2a+4=b+5$
$-2a=b+1$, sebelumnya: $b=-3a$, maka:
$-2a=-3a+1$
$a=1$, maka $b=-3a\Rightarrow b=-3$ diperoleh titik $P(a,b)=P(1,-3)$
Kunci: C
SBMPTN 2018 Matematika IPA Kode 402 No. 3
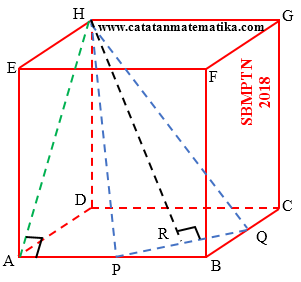
Diketahui kubus ABCD.EFGH dengan panjang rusuk $2\sqrt{2}$ cm. Jika titik $P$ ditengah-tengah AB dan titik Q ditengah-tengah BC, maka jarak antara titik H dengan garis PQ adalah ... cm.
A. $\sqrt{15}$ B. 4 C. $\sqrt{17}$ D. $3\sqrt{2}$ E. $\sqrt{19}$
Pembahasan:
$AB=2\sqrt{2}\Rightarrow PB=\sqrt{2}$
$BC=2\sqrt{2}\Rightarrow BQ=\sqrt{2}$
$PQ=\sqrt{P{{B}^{2}}+B{{Q}^{2}}}\Leftrightarrow PQ=2$
Perhatikan segitiga HAP siku-siku di titik A, $AP=\sqrt{2}$, $AH=4$, maka:
$HP=\sqrt{A{{H}^{2}}+A{{P}^{2}}}$
$HP=\sqrt{{{4}^{2}}+{{(\sqrt{2})}^{2}}}$
$HP=3\sqrt{2}$, $HP=HQ$
Maka garis tinggi HR membagi dua PQ, sehingga $PR=\frac{1}{2}PQ=1$
jarak antara titik H dengan garis PQ adalah panjang HR.
Perhatikan segitiga PRH siku-siku di titik R, maka:
$HR=\sqrt{H{{P}^{2}}+P{{R}^{2}}}$
$HR=\sqrt{{{(3\sqrt{2})}^{2}}-{{1}^{2}}}$
$HR=\sqrt{17}$
Kunci: C
Matematika IPA SBMPTN 2018 Kode 407 No. 4
$\underset{x\to 2}{\mathop{\lim }}\,\frac{\sin (2x-4)}{2-\sqrt{6-x}}$ = …
A. -8 B. -2 C. 0 D. 2 E. 8
Pembahasan:
$\underset{x\to 2}{\mathop{\lim }}\,\frac{\sin (2x-4)}{2-\sqrt{6-x}}$
$=\underset{x\to 2}{\mathop{\lim }}\,\frac{\sin (2x-4)}{2-\sqrt{6-x}}\times \frac{2+\sqrt{6-x}}{2+\sqrt{6-x}}$
$=\underset{x\to 2}{\mathop{\lim }}\,\frac{(2+\sqrt{6-x})\sin (2x-4)}{4-(6-x)}$
$=\underset{x\to 2}{\mathop{\lim }}\,\frac{(2+\sqrt{6-x})\sin 2(x-2)}{(x-2)}$
$=\underset{x\to 2}{\mathop{\lim }}\,(2+\sqrt{6-x})\times \underset{x\to 2}{\mathop{\lim }}\,\frac{\sin 2(x-2)}{(x-2)}$
$=(2+\sqrt{6-2})\times \frac{2}{1}$
$=8$
Kunci: E
Matematika IPA SBMPTN 2018 Kode 407 No. 5
Jika $a+2$, $a-2$, 2 membentuk barisan geometri, maka jumlah 11 suku pertama yang mungkin adalah …
A. 0 B. 1 C. 2 D. 3 E. 4
Pembahasan:
$a+2$, $a-2$, 2
Barisan Geometri:
$U_{2}^{2}={{U}_{1}}\times {{U}_{2}}$
${{(a-2)}^{2}}=(a+2).2$
${{a}^{2}}-4a+4=2a+4$
${{a}^{2}}-6a=0$
$a(a-6)=0$
$a=0$ atau $a=6$
Dengan melihat opsi, kita coba pilih $a=0$, maka barisan $a+2$, $a-2$, 2 menjadi:
2, $-2$, 2, $-2$, 2, $-2$, 2, $-2$, 2, $-2$, 2 (itu 11 suku pertama) yang jika dijumlahkan hasilnya 2.
Kunci: C
Matematika IPA SBMPTN 2018 Kode 407 No. 6
Daerah R dibatasi oleh $y={{x}^{4}}$, $y=1$, $x=2$, dan sumbu X positif. Volume benda putar yang didapat dengan memutar R terhadap sumbu X adalah …
A. $\frac{6}{9}\pi $ B. $\frac{8}{9}\pi $ C. $\frac{10}{9}\pi $ D. $\frac{12}{9}\pi $ E. $\frac{14}{9}\pi $
Pembahasan:
Kunci: C
SBMPTN 2018 Matematika IPA Kode 402 No. 7
Ari dan Ira merupakan anggota dari suatu kelompok yang terdiri dari 9 orang. Banyaknya cara membuat barisan, dengan syarat Ari dan Ira tidak berdampingan, adalah ...
A. $7 \times 8!$ B. $6 \times 8!$ C. $5 \times 8!$ D. $7 \times 7!$ E. $6 \times 7!$
Pembahasan:
Banyak barisan 9 orang secara bebas = 9!
Banyak barisan dengan Ari dan Ira berdampingan = 2!8!
Banyak barisan dengan Ari dan Ira tidak berdampingan adalah:
= 9! – 2!8!
= 9.8! – 2.8!
= 7 x 8!
Kunci: A
Matematika IPA SBMPTN 2018 Kode 407 No. 8
Jika lingkaran ${{x}^{2}}+{{y}^{2}}+2Ax+By=0$ dan ${{x}^{2}}+{{y}^{2}}+Ax+2By=0$ berturut-turut berjari-jari 5 dan 10, maka jari-jari lingkaran ${{x}^{2}}+{{y}^{2}}+Ax+By=0$ adalah …
A. $\sqrt{5}$ B. $\sqrt{10}$ C. 5 D. 10 E. 15
Pembahasan:
Teori: Jika ${{x}^{2}}+{{y}^{2}}+Ax+By+C=0$ maka $r=\sqrt{\frac{{{A}^{2}}+{{B}^{2}}-4C}{4}}$
${{x}^{2}}+{{y}^{2}}+2Ax+By=0$, r = 5, dengan rumus jari-jari lingkaran maka diperoleh:
$5=\sqrt{\frac{{{(2A)}^{2}}+{{B}^{2}}-4.0}{4}}$
$25=\frac{4{{A}^{2}}+{{B}^{2}}}{4}$
$4{{A}^{2}}+{{B}^{2}}=100$ … persamaan (1)
${{x}^{2}}+{{y}^{2}}+Ax+2By=0$, r = 10
$10=\sqrt{\frac{{{A}^{2}}+{{(2B)}^{2}}-4.0}{4}}$
$100=\frac{{{A}^{2}}+4{{B}^{2}}}{4}$
${{A}^{2}}+4{{B}^{2}}=400$… persamaan (2)
Jumlahkan persamaan (1) dan (2), diperoleh:
$5{{A}^{2}}+5{{B}^{2}}=500\Leftrightarrow {{A}^{2}}+{{B}^{2}}=100$
Pertanyaan: jari-jari lingkaran ${{x}^{2}}+{{y}^{2}}+Ax+By=0$?
$r=\sqrt{\frac{{{A}^{2}}+{{B}^{2}}-4.0}{4}}$
$r=\sqrt{\frac{100}{4}}=5$
Kunci: C
Matematika IPA SBMPTN 2018 Kode 407 No. 9
Sisa pembagian $p(x)={{x}^{3}}+a{{x}^{2}}+4x+2b+1$ oleh ${{x}^{2}}+4$ adalah $b-3a$. Jika $p(x)$ habis dibagi oleh $x+1$, maka ${{a}^{2}}+b$ = …
A. 1 B. 3 C. 5 D. 7 E. 9
Pembahasan:
$p(x)={{x}^{3}}+a{{x}^{2}}+4x+2b+1$ habis dibagi oleh $x+1$
$p(-1)={{(-1)}^{3}}+a{{(-1)}^{2}}+4(-1)+2b+1=0$
$-1+a-4+2b+1=0$
$a+2b=4$
$a+2(-1+a)=4$
$a-2+2a=4$
$3a=6\Leftrightarrow a=2$
$b=-1+a\Leftrightarrow b=-1+2=1$
${{a}^{2}}+b={{2}^{2}}+1=5$
Kunci: C
Matematika IPA SBMPTN 2018 Kode 407 No. 10
Jika garis singgung kurva $y=-2{{x}^{3}}$ di titik $P(a,b)$ memotong sumbu $y$ di titik $Q(0,4)$, maka $a+b$ adalah …
A. -1 B. $-\frac{1}{2}$ C. $-\frac{1}{4}$ D. $\frac{1}{4}$ E. 1
Pembahasan:
$P(a,b)$ melalui kurva $y=-2{{x}^{3}}$, maka:
$b=-2{{a}^{3}}$
Garis singgung melalui titik $P(a,b)$ dan (0,4), maka:
$m=\frac{b-4}{a}$
$\frac{dy}{dx}=-6{{x}^{2}}$ titik singgung di $P(a,b)$
$m={{\left. \frac{dy}{dx} \right|}_{x=a}}$
$\frac{b-4}{a}=-6{{a}^{2}}$
$\frac{-2{{a}^{3}}-4}{a}=-6{{a}^{2}}$
$-2{{a}^{3}}-4=-6{{a}^{3}}$
$4{{a}^{3}}=4$
$a=1$
$b=-2{{a}^{3}}\Leftrightarrow b=-{{2.1}^{3}}=-2$
Persamaan garis singgung melalui titik $P(a,b)$ dengan $m=-6{{a}^{2}}$
$y-{{y}_{1}}=m(x-{{x}_{1}})$
$y-b=-6{{a}^{2}}(x-a)$
$a+b=1+(-2)=-1$
Kunci: A
Matematika IPA SBMPTN 2018 Kode 407 No. 11
Jika $\int\limits_{0}^{4}{f(x)dx}=\sqrt{2}$, maka nilai $\int\limits_{0}^{2}{xf({{x}^{2}})dx}$ adalah …
A. $\frac{\sqrt{2}}{4}$ B. $\frac{\sqrt{2}}{2}$ C. $\sqrt{2}$ D. $2\sqrt{2}$ E. $4\sqrt{2}$
Pembahasan:
$\int\limits_{0}^{4}{f(x)dx}=\sqrt{2}$
$\left. F(x) \right|_{0}^{4}=\sqrt{2}$
$F(4)-F(0)=\sqrt{2}$
$\int\limits_{0}^{2}{xf({{x}^{2}})dx}$
Misal:
$u={{x}^{2}}\Leftrightarrow \frac{du}{dx}=2x\Leftrightarrow xdx=\frac{1}{2}du$
Maka:
$\int\limits_{0}^{2}{xf({{x}^{2}})dx}=\int\limits_{x=0}^{x=2}{\frac{1}{2}f(u)du}$
$=\left. \frac{1}{2}F(u) \right|_{x=0}^{x=2}$
$=\left. \frac{1}{2}F({{x}^{2}}) \right|_{x=0}^{x=2}$
$=\frac{1}{2}F({{2}^{2}})-\frac{1}{2}F({{0}^{2}})$
$=\frac{1}{2}\left[ F(4)-F(0) \right]$
$=\frac{1}{2}\sqrt{2}$
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 12
Diketahui $(a_n)$ dan $(b_n)$ adalah dua barisan aritmetika dengan $a_1=5$, $a_2=8$, $b_1=3$, dan $b_2=7$. Jika A = {$a_1$, $a_2$, ..., $a_{100}$} dan B = {$b_1$, $b_2$, ..., $b_{100}$}, maka banyaknya anggota $A\cap B$ adalah ...
A. 20 B. 21 C. 22 D. 23 E. 24
Pembahasan:
$a_1=5$, $a_2=8$, b = 8 – 5 = 3, maka:
$b_1=3$, $b_2=7$, b = 7 – 3 = 4, maka:
A = {5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47
B = {3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47
Jika diperhatikan polanya maka:
$A\cap B$ = {${{a}_{3}}$, ${{a}_{7}}$, ${{a}_{11}}$, …, ${{a}_{n}}$}
Membentuk barisan aritmetika:
3, 7, 11, …, ${{U}_{n}}$
${{U}_{n}}=4n-1\le 100\Leftrightarrow n=25$
Jadi banyak anggota $A\cap B$ adalah 25.
Kunci: Tidak ada opsi
$a_1=5$, $a_2=8$, b = 8 – 5 = 3, maka:
$b_1=3$, $b_2=7$, b = 7 – 3 = 4, maka:
A = {5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47
B = {3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47
Jika diperhatikan polanya maka:
$A\cap B$ = {${{a}_{3}}$, ${{a}_{7}}$, ${{a}_{11}}$, …, ${{a}_{n}}$}
Membentuk barisan aritmetika:
3, 7, 11, …, ${{U}_{n}}$
${{U}_{n}}=4n-1\le 100\Leftrightarrow n=25$
Jadi banyak anggota $A\cap B$ adalah 25.
Kunci: Tidak ada opsi
SBMPTN 2018 Matematika IPA Kode 407 No. 13
Himpunan semua bilangan real $x$ pada selang $\left( \frac{\pi }{2},\frac{3\pi }{2} \right)$ yang memenuhi $\sec x(1+\tan x) < 0$ berbentuk (a, b). Nilai a + b adalah …
A. $\frac{5\pi }{4}$ B. $\frac{7\pi }{4}$ C. $2\pi $ D. $\frac{9\pi }{4}$ E. $\frac{11\pi }{4}$
Pembahasan:
$\sec x(1+\tan x) < 0$
$\frac{1}{\cos x}(1+\frac{\sin x}{\cos x}) < 0$
$\frac{1}{\cos x}.\frac{\cos x+\sin x}{\cos x} < 0$
$\frac{\cos x+\sin x}{{{\cos }^{2}}x} < 0$; karena ${{\cos }^{2}}x > 0$ maka:
$\cos x+\sin x < 0$
Dengan bantuan sketsa gambar! Kita peroleh himpunan penyelesaiannya adalah:
$\left( \frac{3\pi }{4},2\pi \right)=(a,b)$
$a+b=\frac{3\pi }{4}+2\pi =\frac{11\pi }{4}$
Kunci: E
Matematika IPA SBMPTN 2018 Kode 407 No. 14
Himpunan semua nilai $c$ agar grafik $y={{2}^{2{{x}^{2}}+3x-c}}$ dan $y={{4}^{\frac{1}{2}{{x}^{2}}+\frac{1}{2}x+1}}$ berpotongan adalah …
A. {c: $c < -3$ atau $c > 3$}
B. {c: $c < 0$ atau $c > 4$}
C. {c: $c < -3$}
D. {c: $-4 < c < 4$}
E. {c:
Pembahasan:
$y={{2}^{2{{x}^{2}}+3x-c}}$ dan $y={{4}^{\frac{1}{2}{{x}^{2}}+\frac{1}{2}x+1}}$
${{2}^{2{{x}^{2}}+3x-c}}={{4}^{\frac{1}{2}{{x}^{2}}+\frac{1}{2}x+1}}$
${{2}^{2{{x}^{2}}+3x-c}}={{({{2}^{2}})}^{\frac{1}{2}{{x}^{2}}+\frac{1}{2}x+1}}$
${{2}^{2{{x}^{2}}+3x-c}}={{2}^{{{x}^{2}}+x+2}}$
$2{{x}^{2}}+3x-c={{x}^{2}}+x+2$
${{x}^{2}}+2x-c-2=0$, $A=1$, $B=2$, $C=-c-2$ berpotongan maka:
$D>0$
${{b}^{2}}-4ac>0$
${{2}^{2}}-4.1.(-c-2)>0$
$4+4c+8>0$
$4c>-12$
$c>-3$
Kunci: Tidak ada opsi
SBMPTN 2018 Matematika IPA Kode 402 No. 15
Diketahui dua lingkaran $x^2+y^2=2$ dan $x^2+y^2=4$. Garis $l_1$ menyinggung lingkaran pertama di titik $(1,-1)$. Garis $l_2$ menyinggung lingkaran kedua dan tegak lurus dengan garis $l_1$. Titik potong garis $l_1$ dan $l_2$ adalah ...
A. ($1+\sqrt 2$, $\sqrt 2-1$)
B. ($1-\sqrt 2$, $\sqrt 2-1$)
C. ($1+\sqrt 2$, $\sqrt 2+1$)
D. ($1-\sqrt 2$, $\sqrt 2-2$)
E. ($1+\sqrt 2$, $\sqrt 2+2$)
Pembahasan:
${{l}_{1}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=2$ di titik $(1,-1)$ maka:
${{l}_{1}}\equiv {{x}_{1}}.x+{{y}_{1}}.y={{r}^{2}}$
${{l}_{1}}\equiv x-y=2$
${{l}_{1}}\equiv y=x-2\Rightarrow {{m}_{1}}=1$
${{l}_{1}}\bot {{l}_{2}}\Rightarrow {{m}_{1}}.{{m}_{2}}=-1\Leftrightarrow {{m}_{2}}=-1$
${{l}_{2}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=4$ dengan gradien $-1$
$y=mx\pm r\sqrt{{{m}^{2}}+1}$
$y=-x\pm 2\sqrt{2}$
${{l}_{2}}\equiv y=-x+2\sqrt{2}$ atau ${{l}_{2}}\equiv y=-x-2\sqrt{2}$
Titik potong garis ${{l}_{1}}\equiv y=x-2$ dan garis ${{l}_{2}}\equiv y=-x+2\sqrt{2}$ adalah:
$y=y$
$x-2=-x+2\sqrt{2}$
$2x=2+2\sqrt{2}\Leftrightarrow x=1+\sqrt{2}$
$y=x-2$
$y=1+\sqrt{2}-2\Leftrightarrow y=\sqrt{2}-1$
Titik potongnya adalah $\left( 1+\sqrt{2},\sqrt{2}-1 \right)$
Kunci: A
${{l}_{1}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=2$ di titik $(1,-1)$ maka:
${{l}_{1}}\equiv {{x}_{1}}.x+{{y}_{1}}.y={{r}^{2}}$
${{l}_{1}}\equiv x-y=2$
${{l}_{1}}\equiv y=x-2\Rightarrow {{m}_{1}}=1$
${{l}_{1}}\bot {{l}_{2}}\Rightarrow {{m}_{1}}.{{m}_{2}}=-1\Leftrightarrow {{m}_{2}}=-1$
${{l}_{2}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=4$ dengan gradien $-1$
$y=mx\pm r\sqrt{{{m}^{2}}+1}$
$y=-x\pm 2\sqrt{2}$
${{l}_{2}}\equiv y=-x+2\sqrt{2}$ atau ${{l}_{2}}\equiv y=-x-2\sqrt{2}$
Titik potong garis ${{l}_{1}}\equiv y=x-2$ dan garis ${{l}_{2}}\equiv y=-x+2\sqrt{2}$ adalah:
$y=y$
$x-2=-x+2\sqrt{2}$
$2x=2+2\sqrt{2}\Leftrightarrow x=1+\sqrt{2}$
$y=x-2$
$y=1+\sqrt{2}-2\Leftrightarrow y=\sqrt{2}-1$
Titik potongnya adalah $\left( 1+\sqrt{2},\sqrt{2}-1 \right)$
Kunci: A
Soal dan Pembahasan Matematika IPA SBMPTN 2019
Semoga postingan: Pembahasan Matematika IPA SBMPTN 2018 Kode 407 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Pembahasan Matematika IPA SBMPTN 2018 Kode 407"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.