Jurusan Tiga Angka

Konsep Jurusan Tiga Angka (Bering)

Jurusan tiga angka adalah menentukan letak sebuah titik atau obyek yang diukur dari titik atau obyek yang lain, ukuran yang dipakai adalah jarak (r) dan besar sudut ($\alpha$) yang diukur dari arah utara dan searah dengan jarum jam penulisan sudut menggunakan 3 digit (3 angka). Untuk lebih jelasnya perhatikan gambar berikut:


Contoh 1:
Ujian Nasional (UN) SMA Matematika IPA Tahun 2017 No. 28
Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan jurusan tiga angka $120^o$ sejauh 40 km, kemudian berlayar menuju ke pelabuhan C dengan jurusan $240^o$ sejauh 80 km. Jarak antara pelabuhan C dan A adalah ….
A. $20\sqrt{3}$ km
B. 40 km
C. $40\sqrt{3}$ km
D. $40\sqrt{5}$ km
E. $40\sqrt{7}$ km
Pembahasan:
Dari soal dapat kita buat ilustrasi gambar sebagai berikut!



Aturan cosinus:
$\begin{align} b^2 &= a^2+c^2-2ac.\cos B \\ &= 80^2+40^2-2.40.80.\cos 60^o \\ &= 6400+1600-6400.\frac{1}{2} \\ b^2 &= 4800 \\ b &= \sqrt{4800} \\ &= \sqrt{1600x3} \\ b &= 40\sqrt{3} \end{align}$
Jawaban: C

---

Contoh 2:
Sebuah kapal berlayar dari pelabuhan A dengan arah $044^o$ sejauh 50 km. Kemudian berlayar lagi dengan arah $104^o$ sejauh 40 km ke pelabuhan C. Jarak pelabuhan A ke C adalah … cm.
A. $10\sqrt95$
B. $10\sqrt91$
C. $10\sqrt85$
D. $10\sqrt71$
E. $10\sqrt61$
Pembahasan:
Perhatikan gambar sketsa rute kapal dari permasalahan di atas adalah:

$\angle UAB+\angle ABU'={{180}^{o}}$
$44^o+\angle ABU'=180^o$
$\angle ABU'=180^o-44^o$
$\angle ABU'=136^o$
$\angle ABC=360^o-\angle ABU'-\angle U'BC$
$\angle ABC=360^o-136^o-104^o$
$\angle ABC=240^o=\angle B$

Dengan aturan cosinus:
Jarak Pelabuhan A ke Pelabuhan C adalah AC = $b$ = …?
$b^2=a^2+c^2-2ac.\cos B$
$b^2=40^2+50^2-2.40.50.\cos 120^o$
$b^2=1600+2500-2.40.50.\left( -\frac{1}{2} \right)$
$b^2=1600+2500+2000$
$b^2=6100$
$b=\sqrt{6100}$
$b=\sqrt{100\times 61}$
$b=10\sqrt{61}$
Jadi, jarak pelabuhan A ke pelabuhan C adalah $10\sqrt{61}$ km.
Jawaban: E
Untuk lebih jelasnya tonton videonya DISINI.

Contoh 3. UN 2016.
Sebuah kapal mulai bergerak dari pelabuhan A pada pukul 07.00 dengan arah $030^o$ dan tiba di pelabuhan B setelah 4 jam bergerak. Pukul 12.00 kapal bergerak kembali dari pelabuhan B menuju pelabuhan C dengan memutar haluan $150^o$ dan tiba di pelabuhan C pukul 20.00. Kecepatan rata-rata kapal 50 mil/jam. Jarak tempuh kapal dari pelabuhan C ke pelabuhan A adalah ...
A. $200\sqrt2$ mil
B. $200\sqrt3$ mil
C. $200\sqrt6$ mil
D. $200\sqrt7$ mil
E. 600 mil
Pembahasan:
$v_{AB}$ = 50 mil/jam
$t_{AB}$ = 4 jam, maka:
$s_{AB}$ = $v_{AB} \times t_{AB}$
$s_{AB}$ = $50 \times 4$
$s_{AB}$ = 200 mil
$t_{BC}$ = bergerak pukul 12.00 sampai pukul 20.00
$t_{BC}$ = 8 jam
$v_{BC}$ = 50 mil/jam
$s_{BC}$ = $v_{BC} \times t_{BC}$
$s_{BC}$ = $50 \times 8$
$s_{BC}$ = 400 mil
Perhatikan sketsa gambar berikut:

Dengan Aturan Cosinus, maka:$b^2 = a^2 + c^2 -2.a.c.\cos B$
$b^2 = 400^2 + 200^2 - 2.400.200. \cos 60^o$
$b^2 = 40000 + 160000 - 160000. \frac{1}{2}$
$b^2 = 120.000$
$b = 200 \sqrt3$
Jawaban: B

---

Contoh 4. UN 2017
Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan jurusan tiga angka $130^o$ sejauh 20 km. Kemudian berlayar menuju ke pelabuhan C dengan jurusan tiga angka $250^o$ sejauh 40 km. Jarak antara pelabuhan C dan A adalah ...
A. $10\sqrt3$ km
B. $10\sqrt5$ km
C. $20\sqrt3$ km
D. $20\sqrt5$ km
E. $20\sqrt7$ km
Pembahasan:

---

Contoh 5. UN 2017
Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan jurusan tiga angka $080^o$ sejauh 80 km. Kemudian berlayar menuju ke pelabuhan C dengan jurusan $200^o$ sejauh 60 km. Jarak antara pelabuhan C dan A adalah ...
A. 10 km
B. $5\sqrt{13}$ km
C. $10\sqrt{13}$ km
D. $20\sqrt{13}$ km
E. 100 km.
Pembahasan:

---

Contoh 6.
Dua kapal R dan S berjarak 15 km. Kapal S letaknya pada arah $110^o$ dari R dan kapal T, $170^o$ dari R. Jika kapal T letaknya pada arah $245^o$ dari S, maka tentukan jarak kapal T dari kapal S.
Pembahasan:
Perhatikan gambar berikut!

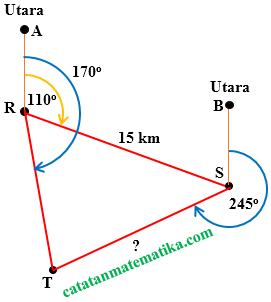
Dari gambar dapat kita peroleh:
$\begin{align} \angle SRT &=\angle ART-\angle ARS \\  &={{170}^{o}}-{{110}^{o}} \\  &={{60}^{o}}  \end{align}$
$\angle BSR$ dan $\angle ARS$ adalah sepasang sudut dalam sepihak, maka:
$\begin{align} \angle BSR + \angle ARS &={180}^{o} \\ \angle BSR + {110}^{o} &={180}^{o} \\ \angle BSR &= {70}^{o} \end{align}$
$\begin{align}  \angle RST &={{360}^{o}}-\angle BSR-\angle BST \\  &={{360}^{o}}-{{70}^{o}}-{{245}^{o}} \\  &={{45}^{o}}  \end{align}$
$\begin{align}  \angle RTS &={{180}^{o}}-\angle SRT-\angle RST \\  &={{180}^{o}}-{{60}^{o}}-{{45}^{o}} \\  &={{75}^{o}}  \end{align}$
Karena kita akan menggunakan aturan sinus maka kita hitung terlebih dahulu $\sin {{75}^{o}}$.
$\begin{align}  \sin {{75}^{o}} &=\sin ({{45}^{o}}+{{30}^{o}}) \\  & =\sin {{45}^{o}}.\cos {{30}^{o}}+\cos {{45}^{o}}.\sin {{30}^{o}} \\  & =\frac{1}{2}\sqrt{2}.\frac{1}{2}\sqrt{3}+\frac{1}{2}\sqrt{2}.\frac{1}{2} \\  & =\frac{1}{4}\left( \sqrt{6}+\sqrt{2} \right)
\end{align}$
Dengan Aturan Sinus:
$\begin{align}  \frac{ST}{\sin \angle SRT} &=\frac{RS}{\sin \angle RTS} \\   \frac{ST}{\sin {{60}^{o}}} &=\frac{15}{\sin {{75}^{o}}} \\   \frac{ST}{\frac{1}{2}\sqrt{3}} &=\frac{15}{\frac{1}{4}\left( \sqrt{6}+\sqrt{2} \right)} \\   ST &=\frac{\frac{15\sqrt{3}}{2}}{\frac{1}{4}\left( \sqrt{6}+\sqrt{2} \right)} \\  ST &=\frac{30\sqrt{3}}{\sqrt{6}+\sqrt{2}} \\   ST &=\frac{30\sqrt{3}}{\sqrt{6}+\sqrt{2}}\times \frac{\sqrt{6}-\sqrt{2}}{\sqrt{6}-\sqrt{2}} \\   ST &=\frac{90\sqrt{2}-30\sqrt{6}}{4} \\   ST &=\frac{1}{2}\left( 45\sqrt{2}-15\sqrt{6} \right)
\end{align}$
Untuk lebih jelasnya silahkan tonton video berikut:

Semoga postingan: Jurusan Tiga Angka ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :