Matriks 4. Determinan dan Invers Matriks 3x3

A. Determinan Matriks 3x3

Aturan Sarrus

Jika matriks $A=\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right)$ maka determinan matriks A adalah: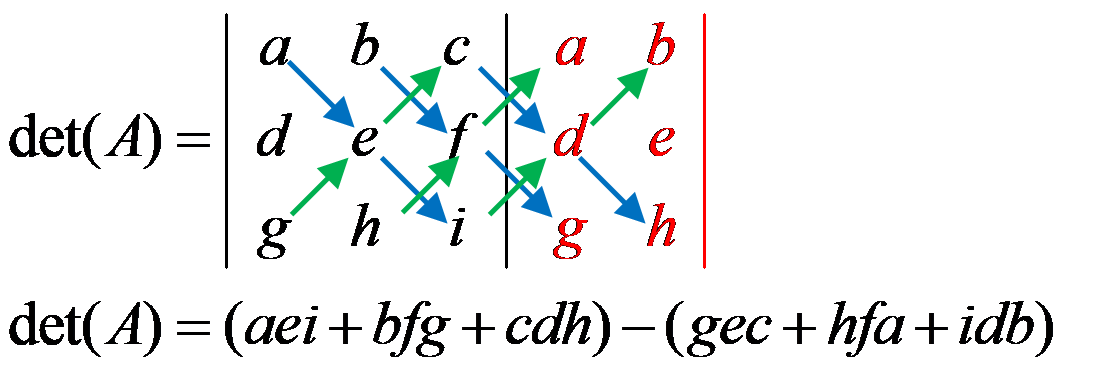

Contoh:
Tentukan determinan dari matriks $A=\left( \begin{matrix} 2 & 3 & 4 \\ 1 & 5 & 7 \\ 6 & 8 & 9 \\ \end{matrix} \right)$.
Penyelesaian:

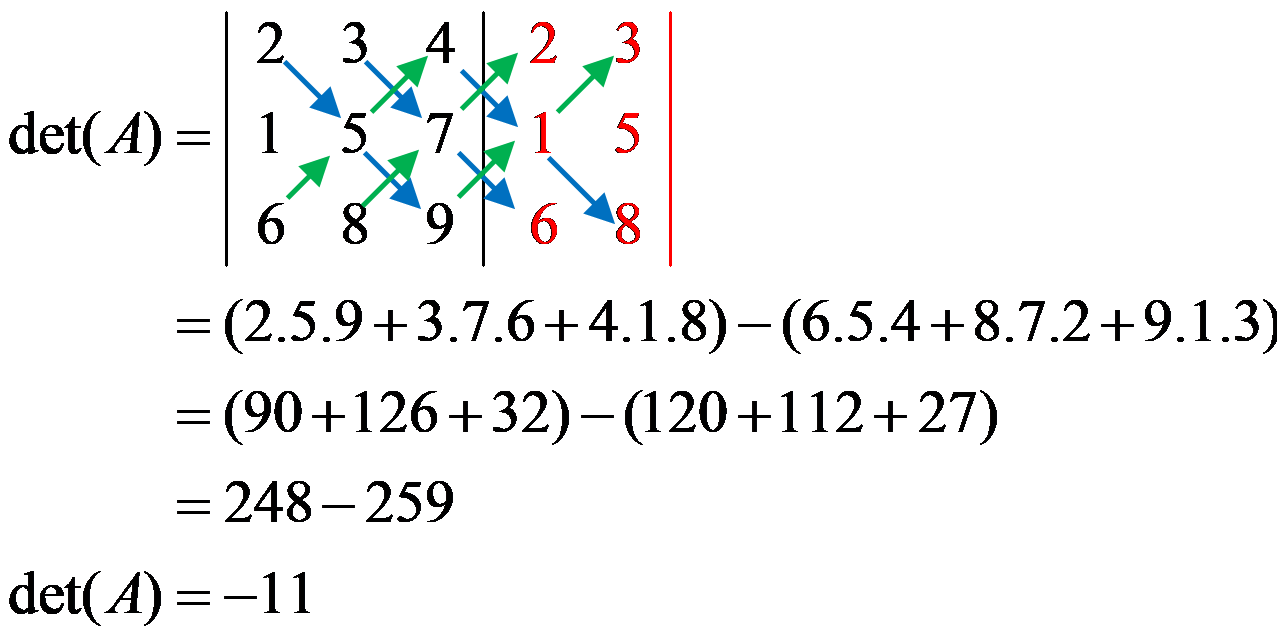
Metode Ekspansi Kofaktor

Determinan matriks $A=\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right)$ dapat juga ditentukan menggunakan metode ekspansi kofaktor.
a. Ekspansi Baris
Ekspansi baris pertama:
$\left| \begin{matrix} \color{red}a & \color{red}b & \color{red}c \\ d & e & f \\ g & h & i \\ \end{matrix} \right|$ = $a\left| \begin{matrix} e & f \\ h & i \\ \end{matrix} \right|-b\left| \begin{matrix} d & f \\ g & i \\ \end{matrix} \right|+c\left| \begin{matrix} d & e \\ g & h \\ \end{matrix} \right|$
Ekspansi baris kedua:
$\left| \begin{matrix} a & b & c \\ \color{red}d & \color{red}e & \color{red}f \\ g & h & i \\ \end{matrix} \right|$ = $-d\left| \begin{matrix} b & c \\ h & i \\ \end{matrix} \right|+e\left| \begin{matrix} a & c \\ g & i \\ \end{matrix} \right|-f\left| \begin{matrix} a & b \\ g & h \\ \end{matrix} \right|$
Ekspansi baris ketiga:
$\left| \begin{matrix} a & b & c \\ d & e & f \\ \color{red}g & \color{red}h & \color{red}i \\ \end{matrix} \right|$ = $g\left| \begin{matrix} b & c \\ e & f \\ \end{matrix} \right|-h\left| \begin{matrix} a & c \\ d & f \\ \end{matrix} \right|+i\left| \begin{matrix} a & b \\ d & e \\ \end{matrix} \right|$

b. Ekspansi Kolom
Ekspansi kolom pertama:
$\left| \begin{matrix} \color{red}a & b & c \\ \color{red}d & e & f \\ \color{red}g & h & i \\ \end{matrix} \right|$ = $a\left| \begin{matrix} e & f \\ h & i \\ \end{matrix} \right|-d\left| \begin{matrix} b & c \\ h & i \\ \end{matrix} \right|+g\left| \begin{matrix} b & c \\ e & f \\ \end{matrix} \right|$
Ekspansi kolom kedua:
$\left| \begin{matrix} a & \color{red}b & c \\ d & \color{red}e & f \\ g & \color{red}h & i \\ \end{matrix} \right|$ = $-b\left| \begin{matrix} d & f \\ g & i \\ \end{matrix} \right|+e\left| \begin{matrix} a & c \\ g & i \\ \end{matrix} \right|-h\left| \begin{matrix} a & c \\ d & f \\ \end{matrix} \right|$
Ekspansi kolom ketiga:
$\left| \begin{matrix} a & b & \color{red}c \\ d & e & \color{red}f \\ g & h & \color{red}i \\ \end{matrix} \right|$ = $c\left| \begin{matrix} d & e \\ g & h \\ \end{matrix} \right|-f\left| \begin{matrix} a & b \\ g & h \\ \end{matrix} \right|+i\left| \begin{matrix} a & b \\ d & e \\ \end{matrix} \right|$

Contoh:
Tentukan determinan dari matriks $A=\left( \begin{matrix} 2 & 3 & 4 \\ 1 & 5 & 7 \\ 6 & 8 & 9 \\ \end{matrix} \right)$ menggunakan metode ekspansi kofaktor kolom ketiga.
Penyelesaian:
$\begin{align} \left| A \right|&=\left| \begin{matrix} 2 & 3 & \color{red}4 \\ 1 & 5 & \color{red}7 \\ 6 & 8 & \color{red}9 \\ \end{matrix} \right| \\ &=\color{red}4\color{black}\left| \begin{matrix} 1 & 5 \\ 6 & 8 \\ \end{matrix} \right|-\color{red}7\color{black}\left| \begin{matrix} 2 & 3 \\ 6 & 8 \\ \end{matrix} \right|+\color{red}9\color{black}\left| \begin{matrix} 2 & 3 \\ 1 & 5 \\ \end{matrix} \right| \\ &=\color{red}4\color{black}(1.8-5.6)-\color{red}7\color{black}(2.8-3.6)+\color{red}9\color{black}(2.5-3.1) \\ &=\color{red}4\color{black}(8-30)-\color{red}7\color{black}(16-18)+\color{red}9\color{black}(10-3) \\ &=\color{red}4\color{black}(-22)-\color{red}7\color{black}(-2)+\color{red}9\color{black}.7 \\ &=-88+14+63 \\ \left| A \right|&=-11 \end{align}$

B. Minor, Kofaktor dan Adjoint Matriks 3x3

Diketahui matriks $A=\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right)$ , maka:
1) Minor matriks ${{A}_{3\times 3}}$
Minor baris ke-1 kolom ke-1:
$M_{11}=\left| \begin{matrix} \color{red}a & \color{red}b & \color{red}c \\ \color{red}d & e & f \\ \color{red}g & h & i \\ \end{matrix} \right|\Rightarrow M_{11}=\left| \begin{matrix} e & f \\ h & i \\ \end{matrix} \right|$
Minor baris ke-1 kolom ke-2:
$M_{12}=\left| \begin{matrix} \color{red}a & \color{red}b & \color{red}c \\ d & \color{red}e & f \\ g & \color{red}h & i \\ \end{matrix} \right|\Rightarrow M_{12}=\left| \begin{matrix} d & f \\ g & i \\ \end{matrix} \right|$
Minor baris ke-1 kolom ke-3:
$M_{13}=\left| \begin{matrix} \color{red}a & \color{red}b & \color{red}c \\ d & e & \color{red}f \\ g & h & \color{red}i \\ \end{matrix} \right|\Rightarrow M_{13}=\left| \begin{matrix} d & e \\ g & h \\ \end{matrix} \right|$
Minor baris ke-2 kolom ke-1:
$M_{21}=\left| \begin{matrix} \color{red}a & b & c \\ \color{red}d & \color{red}e & \color{red}f \\ \color{red}g & h & i \\ \end{matrix} \right|\Rightarrow M_{21}=\left| \begin{matrix} b & c \\ h & i \\ \end{matrix} \right|$
Minor baris ke-2 kolom ke-2:
$M_{22}=\left| \begin{matrix} a & \color{red}b & c \\ \color{red}d & \color{red}e & \color{red}f \\ g & \color{red}h & i \\ \end{matrix} \right|\Rightarrow M_{22}=\left| \begin{matrix} a & c \\ g & i \\ \end{matrix} \right|$
Minor baris ke-2 kolom ke-3:
$M_{23}=\left| \begin{matrix} a & b & \color{red}c \\ \color{red}d & \color{red}e & \color{red}f \\ g & h & \color{red}i \\ \end{matrix} \right|\Rightarrow M_{23}=\left| \begin{matrix} a & b \\ g & h \\ \end{matrix} \right|$
Minor baris ke-3 kolom ke-1:
$M_{31}=\left| \begin{matrix} \color{red}a & b & c \\ \color{red}d & e & f \\ \color{red}g & \color{red}h & \color{red}i \\ \end{matrix} \right|\Rightarrow M_{31}=\left| \begin{matrix} b & c \\ e & f \\ \end{matrix} \right|$
Minor baris ke-3 kolom ke-2:
$M_{32}=\left| \begin{matrix} a & \color{red}b & c \\ d & \color{red}e & f \\ \color{red}g & \color{red}h & \color{red}i \\ \end{matrix} \right|\Rightarrow M_{32}=\left| \begin{matrix} a & c \\ d & f \\ \end{matrix} \right|$
Minor baris ke-3 kolom ke-3:
$M_{33}=\left| \begin{matrix} a & b & \color{red}c \\ d & e & \color{red}f \\ \color{red}g & \color{red}h & \color{red}i \\ \end{matrix} \right|\Rightarrow M_{33}=\left| \begin{matrix} a & b \\ d & e \\ \end{matrix} \right|$

2) Kofaktor matriks ${{A}_{3\times 3}}$
$kof(A)=\left( \begin{matrix} M_{11} & -M_{12} & M_{13} \\ -M_{21} & M_{22} & -M_{23} \\ M_{31} & -M_{32} & M_{33} \\ \end{matrix} \right)$

3) Adjoint Matriks ${{A}_{3\times 3}}$
$adj(A)={{[kof(A)]}^{T}}$

C. Invers Matriks

Invers matriks A adalah ${{A}^{-1}}$ dengan ${{A}^{-1}}=\frac{1}{\det (A)}adj(A)$.
Contoh:
Diketahui matriks $A=\left( \begin{matrix} 1 & 2 & 3 \\ 1 & 3 & 3 \\ 1 & 2 & 4 \\ \end{matrix} \right)$ tentukan ${{A}^{-1}}$.
Penyelesaian:
Determinan matriks A:

Minor matriks A:
$M_{11}=\left| \begin{matrix} 3 & 3 \\ 2 & 4 \\ \end{matrix} \right|=3.4-3.2=\color{red}6$

$M_{12}=\left| \begin{matrix} 1 & 3 \\ 1 & 4 \\ \end{matrix} \right|=1.4-3.1=\color{red}1$

$M_{13}=\left| \begin{matrix} 1 & 3 \\ 1 & 2 \\ \end{matrix} \right|=1.2-3.1=\color{red}-1$

$M_{21}=\left| \begin{matrix} 2 & 3 \\ 2 & 4 \\ \end{matrix} \right|=2.4-3.2=\color{red}2$

$M_{22}=\left| \begin{matrix} 1 & 3 \\ 1 & 4 \\ \end{matrix} \right|=1.4-3.1=\color{red}1$

$M_{23}=\left| \begin{matrix} 1 & 2 \\ 1 & 2 \\ \end{matrix} \right|=1.2-2.1=\color{red}0$

$M_{31}=\left| \begin{matrix} 2 & 3 \\ 3 & 3 \\ \end{matrix} \right|=2.3-3.3=\color{red}-3$

$M_{32}=\left| \begin{matrix} 1 & 3 \\ 1 & 3 \\ \end{matrix} \right|=1.3-3.1=\color{red}0$

$M_{33}=\left| \begin{matrix} 1 & 2 \\ 1 & 3 \\ \end{matrix} \right|=1.3-2.1=\color{red}1$

Kofaktor matriks A:
$kof(A)=\left( \begin{matrix} M_{11} & -M_{12} & M_{13} \\ -M_{21} & M_{22} & -M_{23} \\ M_{31} & -M_{32} & M_{33} \\ \end{matrix} \right)$
$kof(A)=\left( \begin{matrix} 6 & -1 & -1 \\ -2 & 1 & 0 \\ -3 & 0 & 1 \\ \end{matrix} \right)$

Adjoint matriks A:
$adj(A)={{[kof(A)]}^{T}}$
$adj(A)=\left( \begin{matrix} 6 & -2 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{matrix} \right)$

Invers matriks A:
${{A}^{-1}}=\frac{1}{\det (A)}.Adj(A)$
${{A}^{-1}}=\frac{1}{1}\left( \begin{matrix} 6 & -2 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{matrix} \right)$
${{A}^{-1}}=\left( \begin{matrix} 6 & -2 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{matrix} \right)$

D. Soal Latihan

Diketahui matriks $A=\left( \begin{matrix} 1 & 4 & 3 \\ 2 & 5 & 1 \\ 3 & 4 & 2 \\ \end{matrix} \right)$, tentukan:
a. Determinan matriks A
b. Minor matriks A
c. Kofaktor matriks A
d. Adjoint matriks A
e. Invers matriks A

---

Semoga postingan: Matriks 4. Determinan dan Invers Matriks 3x3 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :