Pembahasan Soal SMA Budi Mulia Seleksi Akademik Tahun 2016/2017

Ada postingan baru nih, buat adik-adik yang masih SMP atau yang akan melanjutkan pendidikan ke jenjang SMA favorit/unggulan. Postingan ini adalah Soal dan Pembahasan Matematika masuk SMA Budi Mulia 2016-2017. Soal ini saya dapat dari kiriman WA teman saya. Sebelum kita bahas soal-soalnya sebaiknya kita perlu tahu sekolah bagaimana SMA RK Budi Mulia itu? SMA RK Budi Mulia Pematangsiantar adalah salah satu SMA Favorit. Sekolah ini beralamat di Jl. Melanthon Siregar No. 160, Marihat Jaya, Siantar Marimbun, Kota Pematangsiantar, Sumatera Utara. Untuk bisa lulus/diterima di SMA Budi Mulia Pematangsiantar maka adik-adik harus mempelajari soal tes masuk SMA Budi Mulia Pematangsiantar ini dengan sebaik mungkin.

Berikut ini adalah Soal Tes Masuk SMA Budi Mulia [Pembahasan] tahun pelajaran 2016-2017 Paket A

Soal Masuk SMA Budi Mulia No. 1
Jika:

5 * 2 = 21
8 * 4 = 48
7 * 6 = 13
Maka hasil dari 9 * 7 adalah …
A. 28     B. 30     C. 32     D. 35
Pembahasan:
5 * 2 = (5 + 2)(5 – 2) = 7 x 3 = 21
8 * 4 = (8 + 4)(8 – 4) = 12 x 4 = 48
7 * 6 = (7 + 6)(7 – 6) = 13 x 1 = 13
9 * 7 = (9 + 7)(9 – 7) = 16 x 2 = 32

Kunci: C

Soal Masuk SMA Budi Mulia No. 2
Ayah mempunyai sejumlah uang, $\frac{2}{5}$ dari uang ayah diberikan kepada Toni dan $\frac{3}{8}$ dari uang ayah diberikan kepada Rina, sedangkan sisa uang ayah sekarang adalah Rp. 180.000,00. Besar uang ayah yang diberikan kepada Toni adalah …
A. Rp. 300.000,00
B. Rp. 320.000,00
C. Rp. 330.000,00
D. Rp. 350.000,00
Pembahasan:
Misal: x = jumlah uang ayah sebelum dibagi.
Sisa uang ayah = $x-\frac{2}{5}x-\frac{3}{8}x$
$180.000=x-\frac{2}{5}x-\frac{3}{8}x$ kalikan 40 kedua ruas
$7.200.000=40x-16x-15x$
$7.200.000=9x$
$800.000=x$
Uang yan diberikan kepada Toni adalah:
$=\frac{2}{5}x$
$=\frac{2}{5}\times 800.000$
= 320.000
Kunci: B

Soal Masuk SMA Budi Mulia No. 3
Sebuah pekerjaan dapat diselesaikan dalam waktu 20 hari jika dikerjakan oleh 18 orang. Pada hari ke-5, pekerjaan dihentikan selama 4 hari karena kehabisan bahan baku. Jika pekerjaan itu harus selesai sesuai rencana awal, maka banyak tambahan pekerja yang dibutuhkan adalah …
A. 24 orang
B. 16 orang
C. 8 orang
D. 6 orang
Pembahasan:

Waktu (hari)	Banyak yang bekerja	Hasil pekerjaan (waktu x pekerja)
20	18	360
5	18	90
4	0	0
Sisa: 11	18 + x	270

$11(18+x)=270$
$18+x=24,54$
$x=6,54$
Karena x adalah jumlah pekerja maka x dibulatkan ke atas menjadi 7 tambahan pekerja.
Kunci: Tidak ada opsi

Soal Masuk SMA Budi Mulia No. 4
Jika $\sqrt{2}=a$ dan $\sqrt{3}=b$, maka hasil dari $\sqrt{32}-\sqrt{48}$ adalah …
A. $4a-4b$
B. $4a-3b$
C. $3a-4a$
D. $3a-2a$
Pembahasan:
$\sqrt{32}-\sqrt{48}=\sqrt{16\times 2}-\sqrt{16\times 3}$
$=4\sqrt{2}-4\sqrt{3}$
$=4a-4b$
Kunci: A

Soal Masuk SMA Budi Mulia No. 5
Tiga suku berikutnya dari barisan bilangan 4, 5, 5, 7, 6, 9, 7, …, adalah …
A. 11, 8, 13
B. 11, 13, 15
C. 9, 11, 12
D. 13, 11, 8
Pembahasan:
Kita lompati satu angka:
4, 5, 5, 7, 6, 9, 7, 11, 8, 13.
Pola pertama: selalu ditambah 1 dengan suku sebelumnya diperoleh: 4, 5, 6, 7, 8
Pola kedua: selalu ditambah 2 dengan suku sebelumnya diperoleh: 5, 7, 9, 11, 13
Kunci: A

Soal Masuk SMA Budi Mulia No. 6

Sebuah taman berbentuk persegi panjang dengan ukuran panjang $(3x-1)$ m dan lebar $(x+3)$ m. Jika keliling taman tersebut 68 meter, maka luas taman tersebut adalah … ${{m}^{2}}$

A. 198     B. 208     C. 243     D. 253 

Pembahasan:

Persegipanjang

$K=68$

$2p+2l=68$

$2(3x-1)+2(x+3)=68$

$6x-2+2x+6=68$

$8x=64$

$x=8$

Luas taman adalah:

$=p\times l$

$=(3x-1)\times (x+3)$

$=(3.8-1)\times (8+3)$

$=23\times 11$

$=253$

Kunci: D

Soal Masuk SMA Budi Mulia No. 7

Diketahui himpunan A = {faktor dari 16}. Banyak himpunan bagian dari A yang terdiri dari 3 angka adalah …

A. 12     B. 10     C. 8     D. 6

Pembahasan:

A = {faktor dari 16}

A = {1, 2, 4, 8, 16}, maka n = 5

Banyak himpunan bagian A yang terdiri dari 3 adalah banyak memilih 3 unsur dari 5 unsur.

= C(5, 3)

= $\frac{5!}{3!2!}$

= 10

Kunci: B

Soal Masuk SMA Budi Mulia No. 8

Sebuah fungsi f dinyatakan dengan notasi $f(2x-1)=6x-5$. Nilai dari $f(5)$ adalah …

A. -17     B. -13     C. 13     D. 17

Pembahasan:

$f(2x-1)=6x-5$

Misal: $f(5)=k$maka diperoleh:

Jika $2x-1=5\Leftrightarrow 2x=6\Leftrightarrow x=3$ maka $k=6x-5\Leftrightarrow k=6.3-5=13$

Kunci: C

Soal Masuk SMA Budi Mulia No. 9

Perhatikan gambar!

Grafik garis k tegak lurus dengan grafik garis m dan memotong sumbu X di titik (2,0). Persamaan garis k adalah …
A. $y-2x=-4$
B. $x+2y=1$
C. $x+2y=2$
D. $x-2y=2$

Pembahasan:

Persamaan garis m adalah:

$ax+by=ab$

$-4x+2y=-8$ tegak lurus garis k dan melalui titik (2, 0)

$-4y-2x=-4{{y}_{1}}-2{{x}_{1}}$

$-4y-2x=-4.0-2.2$

$-4y-2x=-4$

$x+2y=2$

Kunci: C

Soal Masuk SMA Budi Mulia No. 10

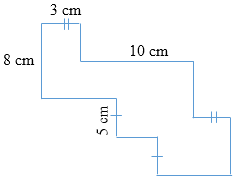
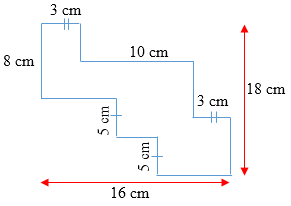
Perhatikan gambar!

Keliling bangun di samping adalah …

A. 72 cm     B. 70 cm     C. 68 cm     D. 66 cm

Pembahasan:

K = 2(16 + 18)

K = 68

Kunci: C

Soal Masuk SMA Budi Mulia No. 11

Perhatikan grafik tarif taxi berikut!

Jika Johny naik taxi sejauh 20 km, maka biaya yang harus ia bayar adalah …

A. Rp. 63.000,00

B. Rp. 65.000,00

C. Rp. 66.000,00

D. Rp. 67.000,00

Pembahasan:

Ambil tiga titik yaitu (4, 19), (7, 28), (20, y)

$(4,19)\Rightarrow {{x}_{1}}=4,{{y}_{1}}=19$

$(7,28)\Rightarrow {{x}_{2}}=7,{{y}_{2}}=28$

$(20,y)\Rightarrow {{x}_{3}}=20,{{y}_{3}}=y$

Karena ketiga titik berada dalam satu garis lurus, maka:

$\frac{{{y}_{3}}-{{y}_{1}}}{{{x}_{3}}-{{x}_{1}}}=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$

$\frac{y-19}{20-4}=\frac{28-19}{7-4}$

$\frac{y-19}{16}=\frac{9}{3}$

$\frac{y-19}{16}=3$

$y-19=48\Leftrightarrow y=67$

Jadi, biaya yang harus dibayar Johny untuk 20 km adalah Rp. 67.000,00

Kunci: D

Soal Masuk SMA Budi Mulia No. 12

Sebuah taman berbentuk persegipanjang dengan ukuran 15 m x 12 m. Di tengah-tengah taman tersebut dibuat kolam ikan yang berbentuk persegi dengan ukuran sisi 5 meter. Di sekeliling kolan ikan dibuat jalan dengan lebar 1 meter. Jika sisa taman akan ditanami rumput, maka luas taman yang akan ditanami rumput adalah … ${{m}^{2}}$

A. 128     B. 130     C. 131     D. 133

Pembahasan:

Perhatikan sketsa gambar berikut!

Luas arsiran adalah:

= 15 x 12 – 7 x 7

= 180 – 49

= 131

Kunci: C

Soal Masuk SMA Budi Mulia No. 13

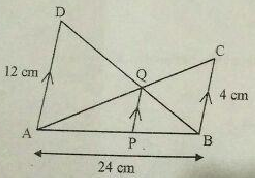
Perhatikan gambar!

Panjang sisi PQ pada gambar adalah … cm

A. 2     B. 2,4     C. 2,8     D. 3 

Pembahasan:

Misalkan panjang AP = x, maka PB = 24 – x

Perhatikan segitiga DBA sebangun dengan QPB, maka:

$\frac{AD}{QP}=\frac{AB}{PB}$

$\frac{12}{QP}=\frac{24}{24-x}$

$24QP=12(24-x)$

$2QP=24-x$

Perhatikan segitiga CBA sebangun dengan segitiga QPA, maka:

$\frac{CB}{QP}=\frac{AB}{AP}$

$\frac{4}{QP}=\frac{24}{x}$

$24QP=4x$

$6QP=x$, substitusi ke:

$2QP=24-x$

$2QP=24-6QP$

$8QP=24\Leftrightarrow QP=3$

Kunci: D

Soal Masuk SMA Budi Mulia No. 14

Perhatikan gambar!

Besar sudut yang ditunjukkan dengan huruf x pada gambar adalah …

A. ${{36}^{o}}$     B. ${{48}^{o}}$     C. ${{58}^{o}}$     D. ${{64}^{o}}$

Pembahasan:

Perhatikan gambar berikut!

$\angle {{A}_{1}}=\angle {{A}_{4}}=x$ (sudut bertolak belakang)
$\angle {{A}_{5}}=\angle {{A}_{3}}={{86}^{o}}$ (sudut sehadap)
$\angle {{A}_{6}}+\angle {{A}_{2}}={{180}^{o}}$
$\angle {{A}_{6}}+\angle {{A}_{2}}={{180}^{o}}$ (sudut dalam sepihak)
$\angle {{A}_{6}}+{{144}^{o}}={{180}^{o}}$
$\angle {{A}_{6}}={{36}^{o}}$
$\angle {{A}_{5}}+\angle {{A}_{4}}+\angle {{A}_{6}}={{180}^{o}}$
${{86}^{o}}+x+{{36}^{o}}={{180}^{o}}\Leftrightarrow x={{58}^{o}}$
Kunci: C

Soal Masuk SMA Budi Mulia No. 15

Rio ingin membuat kerangka balok menggunakan kawat dengan ukuran 12 cm x 10 cm x 8 cm. Jika panjang kawat yang dimiliki Rio 5 meter, maka sisa kawat yang dimiliki Rio adalah … cm

A. 40     B. 30     C. 25     D. 20 

Pembahasan:

Balok: 12 cm x 10 cm x 8 cm

Panjang kawat yang dibutuhkan untuk membuat 1 kerangka kubus adalah:

$=4(p+l+t)$

= 4(12 + 10 + 8)

= 120 cm

Panjang kawat yang tersedia = 5 m = 500 cm

500 = 4 x 120 + Sisa kawat

500 = 480 + Sisa kawat

20 = Sisa kawat

Kunci: D

Soal Masuk SMA Budi Mulia No. 16
Perhatikan gambar!

Gambar di atas adalah sebuah bola yang dimasukkan ke dalam tabung. Jika volume bola 8 liter, maka volume tabung tersebut adalah … liter

A. 10     B. 12      C. 15      D. 16 

Pembahasan:

Volume bola = 8 liter = 8 $d{{m}^{3}}$

${{V}_{bola}}=\frac{4}{3}\pi {{r}^{3}}$ 

$\frac{4}{3}\pi {{r}^{3}}=8$

$\pi {{r}^{3}}=8\times \frac{3}{4}$

$\pi {{r}^{3}}=6$

Tabung: jari-jari alas = r, tinggi tabung = 2r, maka:

${{V}_{tabung}}=\pi {{r}^{2}}t$ 

$=\pi {{r}^{2}}.2r$

$=2.\pi {{r}^{3}}$

= 2.6

= 12 liter

Kunci: B

Soal Masuk SMA Budi Mulia No. 17

Perhatikan gambar!

Gambar di samping adalah sebuah papan nama yang bagian kanan dan kirinya terbuka. Jika victor ingin membuat papan nama tersebut dari bahan kertas karton, maka luas kertas yang diperlukan adalah … $c{{m}^{2}}$

A. 1.920     B. 1.900     C. 1.860    D. 1.800

Pembahasan:

Perhatikan gambar berikut:

$x=\sqrt{{{12}^{2}}+{{9}^{2}}}$

$x=\sqrt{144+81}$

$x=15$

Luas karton yang dibutuhkan adalah:

= keliling segitiga x 40

= (18 + 15 + 15) x 40

= 1920

Kunci: A

Soal Masuk SMA Budi Mulia No. 18

Nilai rata-rata ulangan siswa wanita adalah 78 dan rata-rata ulangan matematika siswa pria adalah 70. Jika rata-rata keseluruhan di kelas itu 73 dan banyak siswa seluruhnya 40 siswa, maka banyak siswa pria di kelas itu adalah … siswa.

A. 15    B. 18    C. 22    D. 25

Pembahasan:

Misal:

${{n}_{1}}$ = jumlah wanita

${{n}_{2}}$ = jumlah pria

${{n}_{1}}+{{n}_{2}}=40\Leftrightarrow {{n}_{1}}=40-{{n}_{2}}$

${{\bar{x}}_{1}}=78$, ${{\bar{x}}_{2}}=70$, ${{\bar{x}}_{total}}=73$, ${{n}_{2}}$ = …?

${{\bar{x}}_{total}}=\frac{{{n}_{1}}.{{{\bar{x}}}_{1}}+{{n}_{2}}.{{{\bar{x}}}_{2}}}{{{n}_{1}}+{{n}_{2}}}$

$73=\frac{(40-{{n}_{2}}).78+{{n}_{2}}.70}{40}$

$73.40=78.40-78{{n}_{2}}+70{{n}_{2}}$

$73.40-78.40=-8{{n}_{2}}$

$-5.40=-8{{n}_{2}}$

$25={{n}_{2}}$

Kunci: D

Soal Masuk SMA Budi Mulia No. 19

Perhatikan diagram lingkaran berikut ini!

Diagram tersebut adalah pembagian kelompok belajar di suatu kelas. Jika banyak siswa yang ada di kelompok B dan F adalah 63 siswa, maka selisih banyak siswa pada kelompok C dan D adalah … siswa.

A. 5    B. 10    C. 15    D. 20

Pembahasan:

A + B + C + D + E + F = ${{360}^{o}}$

${{110}^{o}}+{{60}^{o}}+C+{{45}^{o}}+{{80}^{o}}+{{45}^{o}}={{360}^{o}}$

$C+{{340}^{o}}={{360}^{o}}\Leftrightarrow C={{20}^{o}}$

$D-C=\frac{{}^{o}D-{}^{o}C}{{}^{o}B+{}^{o}F}\times (B+F)$ 

$D-C=\frac{45{}^{o}-20{}^{o}}{60{}^{o}+45{}^{o}}\times 63$

$D-C=15$

Kunci: C

Soal Masuk SMA Budi Mulia No. 20

Seorang ibu mempunyai 2 anak perempuan dan 3 anak laki-laki. Jika ibu itu akan mengajak 2 orang anaknya pergi ke pasar, maka peluang yang diajaknya adalah 1 anak perempuan dan 1 anak laki-laki adalah …

A. $\frac{3}{5}$     B. $\frac{3}{8}$     C. $\frac{3}{10}$      D. $\frac{1}{4}$

Pembahasan:

Seluruh anak = 2 anak perempuan + 3 anak laki-laki = 5 orang anak.

n(S) = banyak cara mengajak 2 orang anak dari 5 orang anak.

$n(S)=C(5,2)$

$n(S)=\frac{5!}{2!3!}=10$

n(A) = banyak cara mengajak 1 anak perempuan dan 1 anak laki-laki.

$n(A)=C(2,1)\times C(3,1)$ 

$n(A)=2\times 3=6$

$P(A)=\frac{n(A)}{n(S)}=\frac{6}{10}=\frac{3}{5}$

Kunci: A

Semoga bermanfaat bagi adik-adik sekalian.

Tetap SEMANGAT....
#Berbagi_Itu_Indah.

Semoga postingan: Pembahasan Soal SMA Budi Mulia Seleksi Akademik Tahun 2016/2017 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :